ЛР1

Пример 1

from sympy import * x = Symbol('x') I = integrate(x**3*exp(x),x) pprint(I)

⎛ 3 2 ⎞ x ⎝x - 3⋅x + 6⋅x - 6⎠⋅ℯ

Упражненеи 1

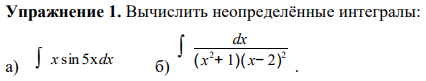
from sympy import * x = Symbol('x') I = integrate(x*sin(5*x)) pprint(I)

x⋅cos(5⋅x) sin(5⋅x) - ────────── + ──────── 5 25

from sympy import * x = Symbol('x') I = integrate(1/((x**2+1)*(x-2)**2)) pprint(I)

⎛ 2 ⎞ 4⋅log(x - 2) 2⋅log⎝x + 1⎠ 3⋅atan(x) 1 - ──────────── + ───────────── + ───────── - ──────── 25 25 25 5⋅x - 10

Упражнение 2

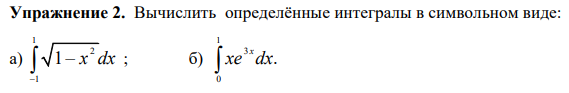
from sympy import * x = Symbol('x') I = integrate(sqrt(1-x**2),(x,1,-1)) pprint(I)

-π ─── 2

from sympy import * import numpy as np x = Symbol('x') I = integrate(x*np.e**(3*x),(x,1,0)) pprint(I)

-4.57456376070837

Упражнение 3

def lr (f,b,a,n,k): x = Symbol('x') dx=(b-a)/n yy=0 for i in np.arange(a,b,dx): yy=yy+f.subs(x,i+dx*k)*dx print(yy) lr(x,2,1,4,0)

1.37500000000000

lr(x,2,1,4,1)

1.62500000000000

Упражнение 4

import numpy as np from sympy import * from scipy import optimize def dn (f,b,a,n): x = Symbol('x') dx=(b-a)/n yy=0 for n in np.arange(a,b,dx): mmin=optimize.fminbound(f,n,n+dx) yy+=mmin*dx return yy ff=lambda x : x dn(ff,2,1,4)

1.3750063126530858

def dv (f,b,a,n): x = Symbol('x') dx=(b-a)/n yy=0 for n in np.arange(a,b,dx): mmin=optimize.fminbound(f,n,n+dx) yy+=mmin*dx return yy ff=lambda x : -x dv(ff,2,1,4)

1.6249936873469142

Упражнение 5

f=np.e**(-x**2) lr(f,2,1,1000,0)

0.135432095059179

lr(f,2,1,1000,1)

0.135082531256897

ff= lambda x : np.e**(-x**2) verx1000=dn(ff,2,1,1000) print(verx1000)

0.1354320950591792

niz1000=dv(ff,2,1,1000) print(niz1000)

0.1350825312568965

Умпражнение 6

import scipy.integrate as integrate import numpy as np x = np.linspace(1,2,1000) s1=integrate.simpson(np.e**(-x**2),x) y=np.linspace(1,2,100) s2=integrate.simpson(np.e**(-y**2),y) print("1000:",s1) print("100:",s2)

1000: 0.13525725799149346 100: 0.13525730090456511

ff= lambda x : np.e**(-x**2) verx100=dn(ff,2,1,100) print(verx100)

0.13701059779474434

ff= lambda x : np.e**(-x**2) niz100=dv(ff,2,1,100) print(niz100)

0.13351495977191724

R1=np.abs(s1-verx1000) print(R1)

0.00017483706768572915

R2=np.abs(s1-niz1000) print(R2)

0.00017472673459695276

R3=np.abs(s2-verx100) print(R3)

0.0017532968901792234

R4=np.abs(s2-niz100) print(R4)

0.0017423411326478733

Упражнение С1

from sympy import * x = Symbol('x') I = integrate(1/(sqrt(x**2+2*x+3))) pprint(I)

⎛√2⋅(x + 1)⎞ asinh⎜──────────⎟ ⎝ 2 ⎠

Упражненеие С2

from sympy import * x = Symbol('x') I = integrate(x*cos(x**2),(x,pi/2,0)) pprint(I)

⎛ 2⎞ ⎜π ⎟ -sin⎜──⎟ ⎝4 ⎠ ───────── 2

Упражнение С3

import numpy as np def lam (f,b,a,n,k): x = Symbol('x') dx=(b-a)/n yy=0 for i in np.arange(a,b,dx): yy=yy+f.subs(x,i+dx*k)*dx print(yy) lam(x,2,1,4,1/2)

1.50000000000000

Индивидуальное задание 1

import numpy as np from sympy import * def lam (f,b,a,n,k): x = Symbol('x') dx=(b-a)/n yy=0 for i in np.arange(a,b,dx): yy=yy+f.subs(x,i+dx*k)*dx print(n,":") print(yy) x = Symbol('x') f=-2*x**3-1 nk=[2,4,8,16,32,64,128,256,512,1024] for k in range(0,10,1): #for n in range (2,1025,2**k): lam(f,-1,-3,nk[k],1)

2 : 16.0000000000000 4 : 26.0000000000000 8 : 31.7500000000000 16 : 34.8125000000000 32 : 36.3906250000000 64 : 37.1914062500000 128 : 37.5947265625000 256 : 37.7971191406250 512 : 37.8984985351563 1024 : 37.9492340087891

Индивидуальное задание 2

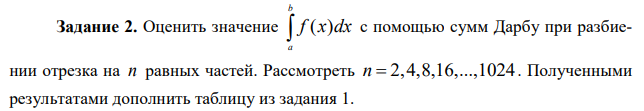
ff= lambda x : -2*x**3-1 nk=[2,4,8,16,32,64,128,256,512,1024] for k in range(0,10,1): print(nk[k],":") dn(ff,-1,-3,nk[k])

2 : 68.0 4 : 52.0 8 : 44.75 16 : 41.3125 32 : 39.640625 64 : 38.81640625 128 : 38.4072265625 256 : 38.203369140625 512 : 38.10162353515625 1024 : 38.05079650878906

ff= lambda x : -2*x**3-1 nk=[2,4,8,16,32,64,128,256,512,1024] for k in range(0,10,1): print(nk[k],":") dv(ff,-1,-3,nk[k])

2 : 16.0 4 : 26.0 8 : 31.75 16 : 34.8125 32 : 36.390625 64 : 37.19140625 128 : 37.5947265625 256 : 37.797119140625 512 : 37.89849853515625 1024 : 37.94923400878906