Упражнение с1

y=sin(x)-cos(x)*x**2 yy=sp.diff(y,x,2) sp.plot(y,adaptive=False, nb_of_points=5000,markers=[{'args':[-8.325,30.579,'r*']},{'args':[-5.406,-17.908,'r*']},{'args':[-2.716,6.306,'r*']},{'args':[-0.515,-0.724,'r*']},{'args':[0.699,0.269,'r*']},{'args':[2.658,6.717,'r*']},{'args':[5.365,-18.267,'r*']},{'args':[8.303,30.792,'r*']}])

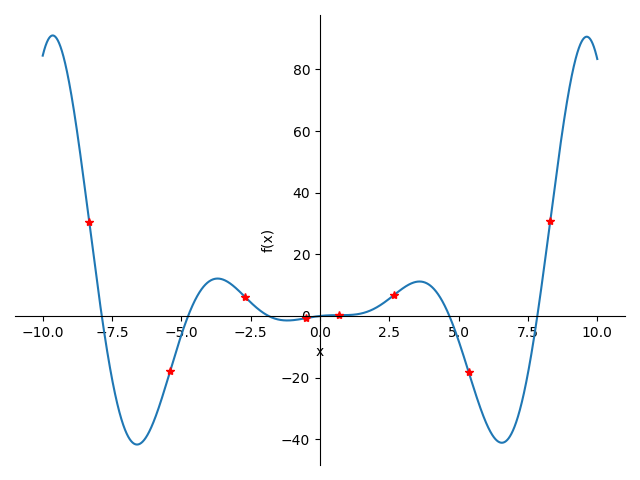
<sympy.plotting.plot.Plot at 0x15211810>

from sympy import * x=Symbol('x') f1=sin(x)-cos(x)*x**2 y1=sp.diff(f1,x,2) print(y1) def f(x): return sin(x)-cos(x)*x**2 def yy(x): return (x**2*cos(x) + 4*x*sin(x) - sin(x) - 2*cos(x)) root1 = optimize.brentq(yy, -9, -8) print('x1 =', round(root1,3)) print('f1 =', round(f(root1),3)) root2 = optimize.brentq(yy, -6, -5) print('x2 =', round(root2,3)) print('f2 =', round(f(root2),3)) root3 = optimize.brentq(yy, -3, -2) print('x3 =', round(root3,3)) print('f3 =', round(f(root3),3)) root4 = optimize.brentq(yy, -1, 0) print('x4 =', round(root4,3)) print('f4 =', round(f(root4),3)) root5 = optimize.brentq(yy, 0, 1) print('x5 =', round(root5,3)) print('f5 =', round(f(root5),3)) root6 = optimize.brentq(yy, 2, 3) print('x6 =', round(root6,3)) print('f6 =', round(f(root6),3)) root7 = optimize.brentq(yy, 5, 6) print('x7 =', round(root7,3)) print('f7 =', round(f(root7),3)) root8 = optimize.brentq(yy, 8, 9) print('x8 =', round(root8,3)) print('f8 =', round(f(root8),3))

x**2*cos(x) + 4*x*sin(x) - sin(x) - 2*cos(x) x1 = -8.325 f1 = 30.579 x2 = -5.406 f2 = -17.908 x3 = -2.716 f3 = 6.306 x4 = -0.515 f4 = -0.724 x5 = 0.699 f5 = 0.269 x6 = 2.658 f6 = 6.717 x7 = 5.365 f7 = -18.267 x8 = 8.303 f8 = 30.792

Упражнение с2

y=np.e**(1/(x**2-1)) sp.plot((y,(x,-5,-1.1)),(y,(x,-1,1)),(y,(x,1.1,5)), xlim=[-5,5], ylim=[-1,3],adaptive=False, nb_of_points=5000,markers=[{'args':[0,0.367,'go']},{'args':[-0.759,0.0938,'r*']},{'args':[0.759,0.0938,'r*']},{'args':[[-1,-1],[-1,3]],'color':'black','ls':'--'},{'args':[[1,1],[-1,3]],'color':'black','ls':'--'},{'args':[[-5,5],[1,1]],'color':'black','ls':'--'},{'args':[[-0.5,-1],[0.3,-0.098]],'color':'maroon','ls':'-'},{'args':[[0.5,1],[0.3,-0.098]],'color':'maroon','ls':'-'}])

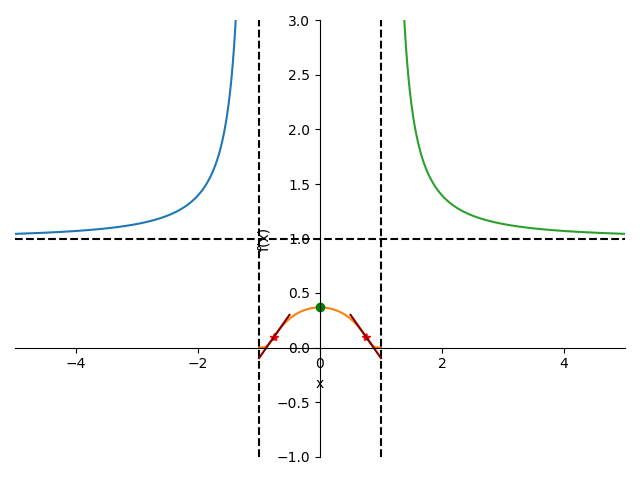
<sympy.plotting.plot.Plot at 0x14a36468>

from sympy import * x=Symbol('x') f1=np.e**(1/(x**2-1)) y1=sp.diff(f1,x,1) print(y1) def f(x): return np.e**(1/(x**2-1)) def yy(x): return (-2.0*2.71828182845905**(1/(x**2 - 1))*x/(x**2 - 1)**2) root1 = optimize.brentq(yy, -0.9, 0.9) print('x1 =', root1) print('f1 =', f(root1))

-2.0*2.71828182845905**(1/(x**2 - 1))*x/(x**2 - 1)**2 x1 = 0.0 f1 = 0.36787944117144233

from sympy import * x=Symbol('x') f1=np.e**(1/(x**2-1)) y1=sp.diff(f1,x,2) print(y1) def yy(x): return (2.71828182845905**(1/(x**2 - 1))*(8.0*x**2/(x**2 - 1) + 4.0*x**2/(x**2 - 1)**2 - 2.0)/(x**2 - 1)**2) root1 = optimize.brentq(yy, -5, 0) print('x1 =', root1) print('f1 =', f(root1)) root2 = optimize.brentq(yy, 0, 5) print('x2 =', root2) print('f2 =', f(root2))

2.71828182845905**(1/(x**2 - 1))*(8.0*x**2/(x**2 - 1) + 4.0*x**2/(x**2 - 1)**2 - 2.0)/(x**2 - 1)**2 x1 = -0.7598356856515821 f1 = 0.09385301377509973 x2 = 0.7598356856515821 f2 = 0.09385301377509973

lim11=sp.limit(((np.e**(1/(x**2-1)))/x),x,sp.oo) lim12=sp.limit(((np.e**(1/(x**2-1)))-lim11*x),x,sp.oo) print(lim11) print(lim12)

0 1

def block (f,x0): x=Symbol('x') ff=f(x) ff1=ff.subs(x,x0) fy=sp.diff(ff,x,1) fy1=fy.subs(x,x0) y=ff1+fy1*(x-x0) print('Касательная:',y) block(f,-0.759)

Касательная: 0.798418985861897*x + 0.700520257329413

block(f,0.759)

Касательная: 0.700520257329413 - 0.798418985861897*x