ЛР11

Пример 1

from scipy import optimize import numpy as np import matplotlib.pyplot as plt def myfun(x): y = 2**x + x return y x = np.linspace(-2, 2, 100) plt.plot(x, myfun(x)) plt.axvline(x=0,color='k') plt.axhline(y=0, color='k') plt.grid() plt.show()

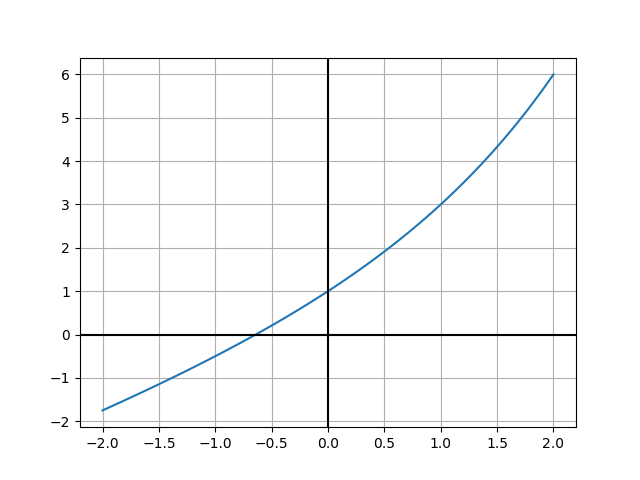
root = optimize.brentq(myfun, -1, 0) print('root =', root) print('f =', myfun(root))

root = -0.641185744504986 f = 0.0

Пример 2

def f(x): return (x-2)**2 + 1 from scipy import optimize minimum = optimize.fmin(f, 1, full_output=True, disp=False) print('x0 =', minimum[0]) print('f(x0) =', minimum[1])

x0 = [2.] f(x0) = 1.0

Упражнение 1

import sympy as sp #from sympy.abc import x def f(x): return (x**4+2*x**2+x+2)/(x**3+2*x**2+x+2) #plt.axvline(x=0,color='k') #plt.axhline(y=0, color='k') y=(x**4+2*x**2+x+2)/(x**3+2*x**2+x+2) sp.plot((y,(x,-7,-2)),(y,(x,-2,4)),adaptive=False, nb_of_points=500, xlim=[-7,4], ylim=[-15,15], markers=[{'args':[-4.185,-8.394,'go']},{'args':[0.679,0.974,'go']},{'args':[0,1,'go']},{'args':[0,1,'r*']},{'args':[0.397,0.986,'r*']},{'args':[[-2,-2],[-15,15]],'color':'black','ls':'--'},{'args':[[-7,4],[-9,2]],'color':'black','ls':'--'},])

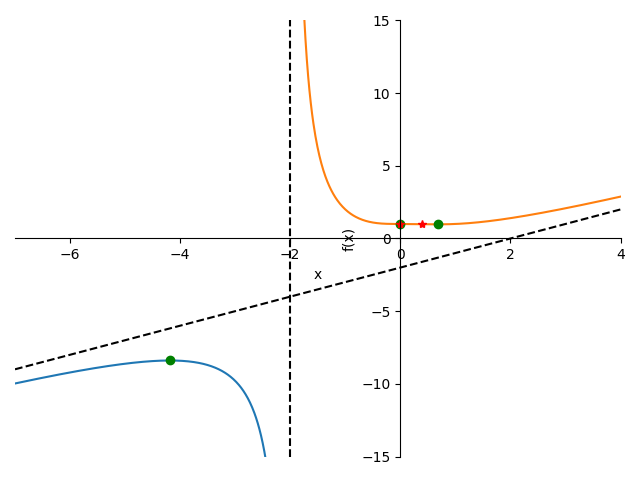
<sympy.plotting.plot.Plot at 0xf0ee3d0>

from sympy import * x=Symbol('x') f1=(x**4+2*x**2+x+2)/(x**3+2*x**2+x+2) y1=sp.diff(f1,x,1) print(y1) def yy(x): return ((-3*x**2 - 4*x - 1)*(x**4 + 2*x**2 + x + 2)/(x**3 + 2*x**2 + x + 2)**2 + (4*x**3 + 4*x + 1)/(x**3 + 2*x**2 + x + 2)) root1 = optimize.brentq(yy, -5, -1) print('root1 =', root1) print('f1 =', f(root1)) root2 = optimize.brentq(yy, -1, 1) print('root2 =', root2) print('f2 =', f(root2)) root3 = optimize.brentq(yy, 0, 1) print('root3 =', root3) print('f3 =', f(root3))

(-3*x**2 - 4*x - 1)*(x**4 + 2*x**2 + x + 2)/(x**3 + 2*x**2 + x + 2)**2 + (4*x**3 + 4*x + 1)/(x**3 + 2*x**2 + x + 2) root1 = -4.1854194331859516 f1 = -8.394597226179426 root2 = 0.6790150493138718 f2 = 0.9743268452212424 root3 = 0.0 f3 = 1.0

from sympy import * x=Symbol('x') f1=(x**4+2*x**2+x+2)/(x**3+2*x**2+x+2) y1=sp.diff(f1,x,2) print(y1) def yy(x): return (2*(6*x**2 - (3*x - (3*x**2 + 4*x + 1)**2/(x**3 + 2*x**2 + x + 2) + 2)*(x**4 + 2*x**2 + x + 2)/(x**3 + 2*x**2 + x + 2) - (3*x**2 + 4*x + 1)*(4*x**3 + 4*x + 1)/(x**3 + 2*x**2 + x + 2) + 2)/(x**3 + 2*x**2 + x + 2)) root1 = optimize.brentq(yy, 0, 5) print('root1 =', root1) print('f1 =', f(root1)) root2 = optimize.brentq(yy, 0.2, 3) print('root2 =', root2) print('f2 =', f(root2))

2*(6*x**2 - (3*x - (3*x**2 + 4*x + 1)**2/(x**3 + 2*x**2 + x + 2) + 2)*(x**4 + 2*x**2 + x + 2)/(x**3 + 2*x**2 + x + 2) - (3*x**2 + 4*x + 1)*(4*x**3 + 4*x + 1)/(x**3 + 2*x**2 + x + 2) + 2)/(x**3 + 2*x**2 + x + 2) root1 = 0.0 f1 = 1.0 root2 = 0.39797689764066996 f2 = 0.9863388080012099

lim11=sp.limit(((x**4+2*x**2+x+2)/(x*(x**3+2*x**2+x+2))),x,sp.oo) lim12=sp.limit((((x**4+2*x**2+x+2)/(x**3+2*x**2+x+2))-lim11*x),x,sp.oo) print(lim11) print(lim12)

1 -2

Упражнение 2

y=sqrt(2/pi)*x**2*np.e**(-x**2/2) sp.plot(y,xlim=[0,10],ylim=[0,1],adaptive=False, nb_of_points=500, markers=[{'args':[1.414,0.587,'go']},{'args':[0.662,0.281,'r*']},{'args':[2.135,0.372,'r*']},{'args':[[0,10],[0,0]],'color':'red','ls':'--'}])

<sympy.plotting.plot.Plot at 0xa896448>

from sympy import * x=Symbol('x') f1=sqrt(2/pi)*x**2*np.e**(-x**2/2) y1=sp.diff(f1,x,1) print(y1) def f(x): return sqrt(2/pi)*x**2*np.e**(-x**2/2) def yy(x): return (-1.0*sqrt(2)*x**3/(2.71828182845905**(x**2/2)*sqrt(pi)) + 2*sqrt(2)*x/(2.71828182845905**(x**2/2)*sqrt(pi))) root1 = optimize.brentq(yy, 0.1, 5) print('root1 =', root1) print('f1 =', round(f(root1),3))

-1.0*sqrt(2)*x**3/(2.71828182845905**(x**2/2)*sqrt(pi)) + 2*sqrt(2)*x/(2.71828182845905**(x**2/2)*sqrt(pi)) root1 = 1.414213562373095 f1 = 0.587

from sympy import * x=Symbol('x') f1=sqrt(2/pi)*x**2*np.e**(-x**2/2) y1=sp.diff(f1,x,2) print(y1) def yy(x): return (sqrt(2)*(1.0*x**2*(x**2 - 1) - 4.0*x**2 + 2)/(2.71828182845905**(x**2/2)*sqrt(pi))) root1 = optimize.brentq(yy, 0, 1) print('root1 =', root1) print('f1 =', round(f(root1),3)) root2 = optimize.brentq(yy, 2, 3) print('root2 =', root2) print('f2 =', round(f(root2),3))

sqrt(2)*(1.0*x**2*(x**2 - 1) - 4.0*x**2 + 2)/(2.71828182845905**(x**2/2)*sqrt(pi)) root1 = 0.6621534468622661 f1 = 0.281 root2 = 2.135779205069857 f2 = 0.372

lim11=sp.limit((sqrt(2/pi)*x**2*np.e**(-x**2/2)/x),x,sp.oo) lim12=sp.limit(((sqrt(2/pi)*x**2*np.e**(-x**2/2))-lim11*x),x,sp.oo) print(lim11) print(lim12)

0 0

y=sqrt(2/pi)*x**2*np.e**(-x**2/2) y1=sqrt(2/pi)*x**2*np.e**(-2*x**2/2)*2**(3/2) sp.plot((y,(x,0,10)),(y1,(x,0,10)),xlim=[0,10],ylim=[0,1],adaptive=False, nb_of_points=500)

<sympy.plotting.plot.Plot at 0x9cdd9e0>

y=sqrt(2/pi)*x**2*np.e**(-x**2/2) y1=sqrt(2/pi)*x**2*np.e**(-0.5*x**2/2)*0.5**(3/2) sp.plot((y,(x,0,10)),(y1,(x,0,10)),xlim=[0,10],ylim=[0,1],adaptive=False, nb_of_points=500)

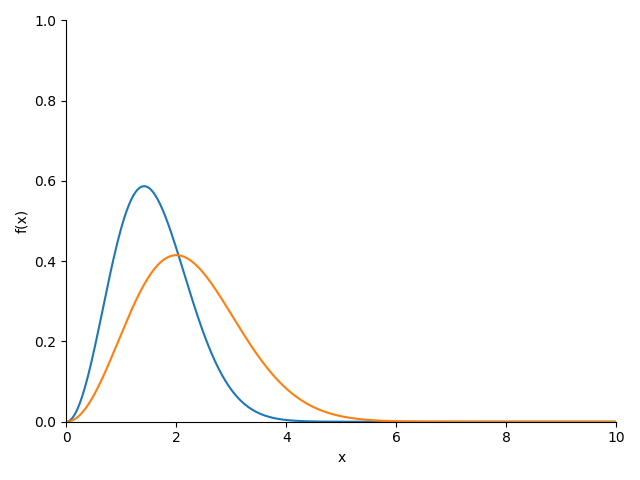
<sympy.plotting.plot.Plot at 0xd1507d0>