ЛР10

Упражнение 1

import numpy as np import sympy as sp from sympy import * x=Symbol('x') def fa(x): return sp.cos(x) f = open('tt1.txt','w') f.write('ТАБЛИЦА ЗНАЧЕНИЙ ПРОИЗВОДНОЙ ФУНКЦИИ sin x\n'); f.write(' ______________\n') f.write('| N | Производная |\n') f.write(' ______________\n') for i in np.arange(1,6): x=Symbol('x') ff=fa(x) yy=sp.diff(ff,x,i) t=1 yx=round(yy.subs(x,t),7) print(yy) f.write("| {i:1.0f} | {yx} |\n".format(i=i, yx=yx)) f.close()

-sin(x) -cos(x) sin(x) cos(x) -sin(x)

Упражнение 2

import sympy as sp import numpy as np from sympy import * def proiz(f,x0,n): y=np.zeros(n) yy=np.zeros(n) x=Symbol('x') for i in np.arange(0,n): a=sp.diff(f,x,i) y[i]=a.subs(x,x0) return y x=Symbol('x') print(proiz(cos(x),0,9)) print(proiz(sin(x),0,9)) print(proiz(log(x+1),0,9))

[ 1. 0. -1. 0. 1. 0. -1. 0. 1.] [ 0. 1. 0. -1. 0. 1. 0. -1. 0.] [ 0.00e+00 1.00e+00 -1.00e+00 2.00e+00 -6.00e+00 2.40e+01 -1.20e+02 7.20e+02 -5.04e+03]

Упражнение 3

import sympy as sp import numpy as np from sympy import * def tlr(m): x=Symbol('x') x0=m[0] n=m[1] l=m[2] f=0 for i in np.arange(0,n): f=(l[i]*(x-x0)**i)/sp.factorial(i) return f x=Symbol('x') m=[0, 1,proiz(sin(x),0,2)] tlr(m)

0

x=Symbol('x') m=[0, 2,proiz(sin(x),0,3)] tlr(m)

1.0*x

x=Symbol('x') m=[0, 3,proiz(sin(x),0,3)] tlr(m)

0

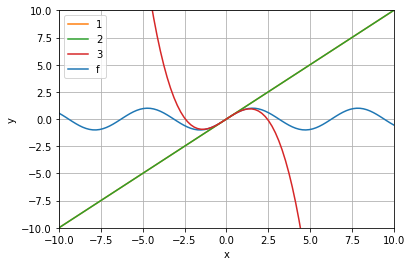
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import approximate_taylor_polynomial x = np.linspace(-10.0, 10.0, num=100) def ff(x): return np.sin(x) h4,=plt.plot(x, np.sin(x), label="f") #for degree in np.arange(1, 4): #sin_taylor = approximate_taylor_polynomial(ff, 0, degree,1, order=degree + 2) #plt.plot(x, sin_taylor(x), label=f"degree={degree}") h1,=plt.plot(x,x,label="1") h2,=plt.plot(x,x,label="2") h3,=plt.plot(x,x-x**3/6,label="3") #plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.0, shadow=True) #plt.tight_layout() plt.legend(handles=[h1,h2,h3,h4]) plt.axis([-10, 10, -10, 10]) plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show()

import sympy as sp import numpy as np from sympy import * def tlr(m): x=Symbol('x') x0=m[0] n=m[1] l=m[2] f=0 for i in np.arange(0,n): f=(l[i]*(x-x0)**i)/sp.factorial(i) return f x=Symbol('x') m=[0, 1,proiz(cos(x),0,2)] tlr(m)

1.00000000000000

x=Symbol('x') m=[0, 2,proiz(cos(x),0,3)] tlr(m)

0

x=Symbol('x') m=[0, 3,proiz(cos(x),0,4)] tlr(m)

-0.5*x**2

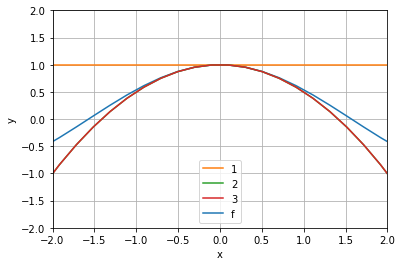
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import approximate_taylor_polynomial x = np.linspace(-10.0, 10.0, num=100) def ff(x): return np.cos(x) h4,=plt.plot(x, np.cos(x), label="f") h1,=plt.plot([-2,2],[1,1],label="1") h2,=plt.plot(x,1-x**2/2,label="2") h3,=plt.plot(x,1-x**2/2,label="3") #for degree in np.arange(1, 4): #sin_taylor = approximate_taylor_polynomial(ff, 0, degree,1, order=degree + 2) #plt.plot(x, sin_taylor(x), label=f"degree={degree}") #plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.0, shadow=True) #plt.tight_layout() plt.legend(handles=[h1,h2,h3,h4]) plt.axis([-2, 2, -2, 2]) plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show()

import sympy as sp import numpy as np from sympy import * def tlr(m): x=Symbol('x') x0=m[0] n=m[1] l=m[2] f=0 for i in np.arange(0,n): f=(l[i]*(x-x0)**i)/sp.factorial(i) return f x=Symbol('x') m=[0, 1,proiz(log(x+4),0,1)] tlr(m)

1.38629436111989

x=Symbol('x') m=[0, 2,proiz(log(x+4),0,2)] tlr(m)

0.25*x

x=Symbol('x') m=[0, 3,(log(x+4),0,3)] tlr(m)

3*x**2/2

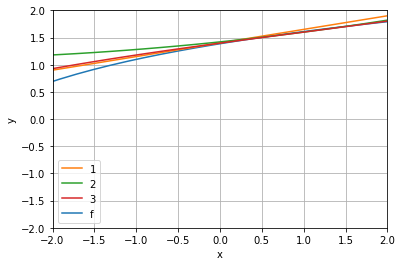
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import approximate_taylor_polynomial x = np.linspace(-10.0, 10.0, num=100) def ff(x): return np.log(x+4) h4,=plt.plot(x,np.log(x+4), label="f") h1,=plt.plot(x,x/4+1.4,label="1") h2,=plt.plot(x,x/5+1.4+(x-1)**2/50,label="2") h3,=plt.plot(x,x/5+1.4+(x-1)**3/375,label="3") #for degree in np.arange(1, 4): #sin_taylor = approximate_taylor_polynomial(ff, 0, degree,1, order=degree + 2) #plt.plot(x, sin_taylor(x), label=f"degree={degree}") #plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.0, shadow=True) #plt.tight_layout() plt.axis([-2, 2, -2, 2]) plt.legend(handles=[h1,h2,h3,h4]) plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show()

Упражнение С1

import sympy as sp import numpy as np from sympy import * def tlr(m): x=Symbol('x') x0=m[0] n=m[1] l=m[2] f=0 for i in np.arange(0,n): f=(l[i]*(x-x0)**i)/sp.factorial(i) return f x=Symbol('x') m=[0, 1,proiz(sqrt(x+4),0,1)] tlr(m)

2.00000000000000

x=Symbol('x') m=[0, 2,proiz(sqrt(x+4),0,2)] tlr(m)

0.25*x

x=Symbol('x') m=[0, 3,(sqrt(x+4),0,3)] tlr(m)

3*x**2/2

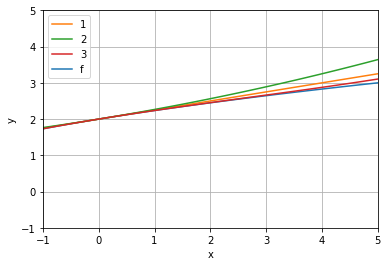
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import approximate_taylor_polynomial x = np.linspace(-10.0, 10.0, num=100) def ff(x): return np.sqrt(x+4) h4,=plt.plot(x, np.sqrt(x+4), label="f") h1,=plt.plot(x,x/4+2,label="1") h2,=plt.plot(x,0.01562*x**2 + 0.25*x + 2,label="2") h3,=plt.plot(x,0.001961*x**3 - 0.01562*x**2 + 0.25*x + 2,label="3") #for degree in np.arange(1, 4): #sin_taylor = approximate_taylor_polynomial(ff, 0, degree,1, order=degree + 2) #plt.plot(x, sin_taylor(x), label=f"degree={degree}") #plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.0, shadow=True) #plt.tight_layout() plt.axis([-1, 5, -1, 5]) plt.legend(handles=[h1,h2,h3,h4]) plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show()

Упражнение С2

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.sin(x) f=approximate_taylor_polynomial(ff, 0, 7,1, order=degree + 2) print(f)

7 6 5 4 3 -0.0001983 x - 3.323e-15 x + 0.008333 x + 2.313e-15 x - 0.1667 x 2 - 4.329e-16 x + 1 x - 5.964e-17

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.cos(x) f=approximate_taylor_polynomial(ff, 0, 7,1, order=degree + 2) print(f)

7 6 5 4 3 5.387e-07 x - 0.001389 x - 3.536e-07 x + 0.04167 x + 8.418e-08 x 2 - 0.5 x - 5.261e-09 x + 1

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.e**x f=approximate_taylor_polynomial(ff, 0, 7,1, order=degree + 2) print(f)

7 6 5 4 3 2 0.0001978 x + 0.001389 x + 0.008334 x + 0.04167 x + 0.1667 x + 0.5 x + 1 x + 1

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.log(x+1) f=approximate_taylor_polynomial(ff, 0, 7,1, order=degree + 2) print(f)

7 6 5 4 3 2 0.2054 x + 1.934 x - 0.5882 x - 0.8428 x + 0.618 x - 0.4607 x + 0.9799 x - 1.52e-16

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.tan(x) f=approximate_taylor_polynomial(ff, 0, 7,1, order=degree + 2) print(f)

7 6 5 4 3 -0.0509 x + 2.451e-13 x + 0.1912 x - 1.044e-13 x + 0.3208 x 2 + 1.175e-14 x + 1.001 x - 3.783e-16

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.sin(x) f=approximate_taylor_polynomial(ff, np.pi, 5,1, order=degree + 2) print(f)

5 4 3 2 -0.008333 x - 5.245e-16 x + 0.1667 x + 4.232e-16 x - 1 x + 9.411e-17

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.cos(x) f=approximate_taylor_polynomial(ff, np.pi, 5,1, order=degree + 2) print(f)

5 4 3 2 3.536e-07 x - 0.04167 x - 8.418e-08 x + 0.5 x + 5.261e-09 x - 1

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.log(x+4) f=approximate_taylor_polynomial(ff, 0, 4,1, order=degree + 2) print(f)

4 3 2 -0.001019 x + 0.005242 x - 0.03124 x + 0.25 x + 1.386

from scipy.interpolate import approximate_taylor_polynomial def ff(x): return np.sqrt(x+4) f=approximate_taylor_polynomial(ff, 0, 4,1, order=degree + 2) print(f)

4 3 2 -0.0003155 x + 0.001961 x - 0.01562 x + 0.25 x + 2