ЛР9

Пример 1

import numpy as np pol = [1, 0 , 5, 7, 8, 3] print(f"Значение полинома в точке x = -2 равно {np.polyval(pol, -2)}.")

Значение полинома в точке x = -2 равно -57.

Упражнение 1

import numpy as np pol = [1,0,0,3.2,0,3,0,3] print(f"Значение полинома в точке x = -1 равно {np.polyval(pol, -1)}.") print(f"Значение полинома в точке x = 4 равно {np.polyval(pol, 4)}.") print(f"Значение полинома в точке x = 2.2 равно {np.polyval(pol, 2.2)}.") print(f"Значение полинома в точке x = pi равно {np.polyval(pol, np.pi)}.")

Значение полинома в точке x = -1 равно 8.2. Значение полинома в точке x = 4 равно 17254.2. Значение полинома в точке x = 2.2 равно 341.91770880000024. Значение полинома в точке x = pi равно 3364.6111322888664.

Пример 2

import numpy as np pol = [1, 0, 5, 7, 8, 3] print(f"Корни полинома равны:") for root in np.roots(pol): print(f"{root : .3f}")

Корни полинома равны: 0.759+2.283j 0.759-2.283j -0.500+0.866j -0.500-0.866j -0.518+0.000j

Пример 3

import numpy as np pol = [1, 0, 5, 7, 8, 3] print(f"Коэффициенты полинома равны:") for root in np.poly(np.roots(pol)): print(f"{root : .3f}")

Коэффициенты полинома равны: 1.000 -0.000 5.000 7.000 8.000 3.000

np.poly([0.7592 + 2.2827j, 0.7592 - 2.2827j, -0.5000 + 0.8660j, -0.5000 - 0.8660j, -0.5184])

array([1. , 0. , 4.99992137, 7.00004405, 7.99978005, 2.99990268])

np.poly([0.759 + 2.283j, 0.759 - 2.283j, -0.500 + 0.866j, -0.500 - 0.860j, -0.518])

array([1. +0.j , 0. -0.006j , 4.996606 +0.003j , 7.00535806-0.02701108j, 7.97390839-0.03299517j, 2.98256111-0.00899482j])

Упражнение 2

import numpy as np pol = [2,0,0,-3,0,0,7,0,-2] print(f"Корни полинома равны:") for root in np.roots(pol): print(f"{root : .4f}")

Корни полинома равны: -0.9586+0.7952j -0.9586-0.7952j -0.1514+1.2536j -0.1514-1.2536j 1.0927+0.4678j 1.0927-0.4678j -0.5179+0.0000j 0.5525+0.0000j

import numpy as np pol = [2, 0, 0, -3, 0, 0, 7, 0, -2] print(f"Коэффициенты полинома равны:") for root in np.poly(np.roots(pol)): print(f"{root : .3f}")

Коэффициенты полинома равны: 1.000 0.000 -0.000 -1.500 -0.000 0.000 3.500 -0.000 -1.000

np.poly([-0.9586+0.7952j, -0.9586-0.7952j, -0.1514+1.2536j, -0.1514-1.2536j, 1.0927+0.4678j,1.0927-0.4678j,-0.5179,0.5525])

array([ 1.00000000e+00, 2.22044605e-16, 1.25300000e-04, -1.50007385e+00, -1.12978023e-04, -3.93063584e-04, 3.50024588e+00, 9.28803415e-05, -9.99904892e-01])

Упражнение 3

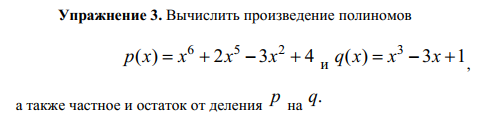
p=[1,2,0,0,-3,0,4] q=[1,0,-3,1] print("Умножение:",np.convolve(p,q)) print("Деление:",np.polydiv(p,q))

Умножение: [ 1 2 -3 -5 -1 0 13 -3 -12 4] Деление: (array([1., 2., 3., 5.]), array([ 4., 12., -1.]))

Упражнение 4

import numpy as np def summa(p, q): x=len(p) y=len(q) print(x) print(y) if x>y: n=np.zeros(x-y) m=np.hstack((n, q)) s=p+m if x<y: n=np.zeros(y-x) m=np.hstack((n, p)) s=q+m if x==y: s=p+q return s p=[1, 2, 0, 0, -3, 0, 4] q=[1, 0, -3, 1] summa(p,q)

7 4

array([ 1., 2., 0., 1., -3., -3., 5.])

Упражнение 5

import numpy as np p=[1,-1,0,-3,0,-2] q=[1,0,0,0,0,-3,1] y=np.convolve(p,q) d=np.polydiv(q,p) print("Производная p:",np.polyder(p)) print("Производная q:",np.polyder(q)) print("Производная произведения:",np.polyder(y)) print("Производная деления:",np.polyder(d))

Производная p: [ 5 -4 0 -6 0] Производная q: [ 6 0 0 0 0 -3] Производная произведения: [ 11 -10 0 -24 0 -30 20 -4 27 -6 6]

/lib/python3.10/site-packages/numpy/lib/polynomial.py:436: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray. p = NX.asarray(p)

Производная деления: [array([1., 1.])]

Пример 4

import numpy as np import matplotlib.pyplot as plt x = 2 * np.pi * np.linspace(0, 1, 60) for a in 0.2 * np.linspace(0, 1, 10) - 0.1: y = np.exp(-a * x) * np.sin(x) plt.plot(x, y, label=f"{a = : .2f}") plt.legend() plt.show()

Упражнение 6

def pr (p, n): pp=np.polyder(p,n) return pp p=[1, 0, 0, -1, 0, 0, 0, 0, 3, 0, -2] n=5 z=pr(p,n) print(z) np.polyval(z, 0.2)

[30240 0 0 -2520 0 0]

-91.1232

Упражнение 7

import sympy as sp import numpy as np import matplotlib.pyplot as plt def teilor (p,x0): n=len(p) T=np.zeros(n-1) for i in np.arange(1,n,1): p=np.polyder(p) z=np.polyval(p,x0) T[n-i-1]=z/(sp.factorial(i)) return T p=[1, 0, 2, 0, 0, -3, -2] x=teilor(p,-1) print(x) y=teilor(p,2) print(y)

[ 1. -6. 17. -28. 27. -17.] [ 1. 12. 62. 176. 288. 253.]

Упражнение С1

import numpy as np pol = [1,0,0,0,0,0,-1] print(f"Корни полинома равны:") for root in np.roots(pol): print(f"{root : .4f}")

Корни полинома равны: -1.0000+0.0000j -0.5000+0.8660j -0.5000-0.8660j 0.5000+0.8660j 0.5000-0.8660j 1.0000+0.0000j

import numpy as np pol = [1,0,0,0,0,0,-1] print(f"Коэффициенты полинома равны:") for root in np.poly(np.roots(pol)): print(f"{root : .3f}")

Коэффициенты полинома равны: 1.000 0.000 -0.000 -0.000 -0.000 0.000 -1.000

Упражнение С2

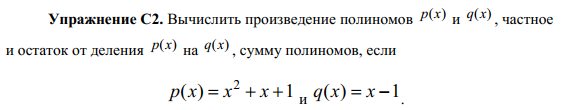
p=[1,1,1] q=[1,-1] print("Умножение:",np.convolve(p,q)) print("Деление:",np.polydiv(p,q))

Умножение: [ 1 0 0 -1] Деление: (array([1., 2.]), array([3.]))

import numpy as np def summa(p, q): x=len(p) y=len(q) print(x) print(y) if x>y: n=np.zeros(x-y) m=np.hstack((n, q)) s=p+m if x<y: n=np.zeros(y-x) m=np.hstack((n, p)) s=q+m if x==y: s=p+q return s p=[1,1,1] q=[1,-1] summa(p,q)

3 2

array([1., 2., 0.])

Упражнение С3

import sympy as sp def teilor (p,x0): n=len(p); T=np.zeros(n) for i in np.arange(1,n,1): p=np.polyder(p) z=np.polyval(p,x0) T[i]=z/(sp.factorial(i)) return T p=[1,-2,0,1] teilor(p,-2)

array([ 0., 20., -8., 1.])