ЛР8

Упражнение 1

import numpy as np from sympy import * def prir (f, x, n, c, sh): f=x**2 dx=np.arange(n,c+sh,sh) df=(x+dx)**2-f return df x=Symbol('x') f=x**2 print("1:",prir(f,0,0,1,0.1)) print("2:",prir(f,2,0,1,0.1)) print("3:",prir(f,-9,0,1,0.1))

1: [0. 0.01 0.04 0.09 0.16 0.25 0.36 0.49 0.64 0.81 1. ] 2: [0. 0.41 0.84 1.29 1.76 2.25 2.76 3.29 3.84 4.41 5. ] 3: [ 0. -1.79 -3.56 -5.31 -7.04 -8.75 -10.44 -12.11 -13.76 -15.39 -17. ]

Упражнение 2

def prir_2(f,x,n,c,sh): f=1/x dx=dx=np.arange(n,c+sh,sh) df=(1/(x+dx))-f return df x=Symbol('x') f=1/x prir_2(f,1,-0.5,0.5,0.05)

array([ 1.00000000e+00, 8.18181818e-01, 6.66666667e-01, 5.38461538e-01, 4.28571429e-01, 3.33333333e-01, 2.50000000e-01, 1.76470588e-01, 1.11111111e-01, 5.26315789e-02, 2.22044605e-16, -4.76190476e-02, -9.09090909e-02, -1.30434783e-01, -1.66666667e-01, -2.00000000e-01, -2.30769231e-01, -2.59259259e-01, -2.85714286e-01, -3.10344828e-01, -3.33333333e-01])

Упражнение 3

def otn(x,dx): dy=np.sqrt(x+dx)-np.sqrt(x) d=dy/dx return d x=Symbol('x') dx=np.array([0.1,0.01, 0.001]) print("1:",otn(1,dx)) print("2:",otn(0.5,dx)) print("3:",otn(2,dx))

1: [0.48808848 0.49875621 0.49987506] 2: [0.67489888 0.70360617 0.70675358] 3: [0.34924112 0.35311255 0.35350921]

Упражнение 4

import numpy as np import sympy as sp from sympy import * def f1(x): return x**(1/3) def f2(x): return 2**x def zn_f(f,t,dx): dy1=f(t+dx)-f(t) dy2=f(t-dx)-f(t) d=np.array([dy1/dx, dy2/(-dx)]) return d dx=0.001 x=Symbol('x') print('1.1:',zn_f(f1,1,dx)) print('1.2:',zn_f(f1,2,dx)) print('1.3:',zn_f(f1,-3,dx)) print('2.1:',zn_f(f2,1,dx)) print('2.2:',zn_f(f2,2,dx)) print('2.3:',zn_f(f2,-3,dx))

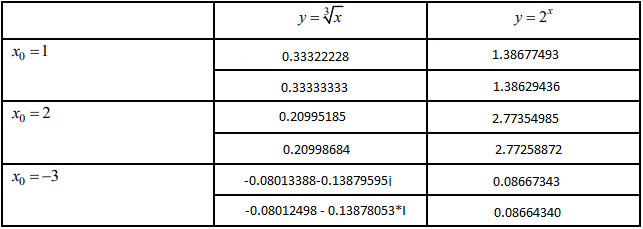
1.1: [0.33322228 0.33344451] 1.2: [0.20995185 0.21002185] 1.3: [-0.08013388-0.13879595j -0.08011608-0.13876511j] 2.1: [1.38677493 1.38581402] 2.2: [2.77354985 2.77162804] 2.3: [0.08667343 0.08661338]

Упражнение 5

import numpy as np import sympy as sp from sympy import * def f1(x): return x**(1/3) def f2(x): return 2**x def zn_ff(f,t): x=Symbol('x') dx=Symbol('dx') dy=f(x+dx)-f(x) y=sp.limit(dy/dx,dx,0) yy=y.subs(x,t) y1=round(yy,8) return y1 print('1.1:',zn_ff(f1,1)) print('1.2:',zn_ff(f1,2)) print('1.3:',zn_ff(f1,-3)) print('2.1:',zn_ff(f2,1)) print('2.2:',zn_ff(f2,2)) print('2.3:',zn_ff(f2,-3))

1.1: 0.33333333 1.2: 0.20998684 1.3: -0.08012498 - 0.13878053*I 2.1: 1.38629436 2.2: 2.77258872 2.3: 0.08664340

Упражнение 6

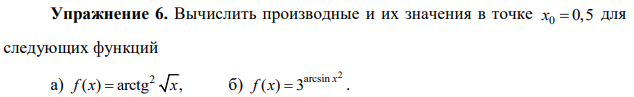
from sympy import * x=Symbol('x') f1=(sp.acot(sp.sqrt(x)))**2 y1=sp.diff(f1,x,1) yy1=y1.subs(x,0.5) fy1=sp.diff(f1,x,1) print(fy1) print("a:",yy1) f2=3**(sp.asin(x**2)) y2=sp.diff(f2,x,1) yy2=y2.subs(x,0.5) fy2=sp.diff(f2,x,1) print(fy2) print("b:",yy2)

-acot(sqrt(x))/(sqrt(x)*(x + 1)) a: -0.900681145141387 2*3**asin(x**2)*x*log(3)/sqrt(1 - x**4) b: 1.36324364610782*log(3)

Упражнение 7

import matplotlib.pyplot as plt def f1(x): return (sp.cos(3*x))**3 def f2(x): return np.e**(2*x) def block (f,x0): x=Symbol('x') ff=f(x) ff1=ff.subs(x,x0) fy=sp.diff(ff,x,1) fy1=fy.subs(x,x0) y=ff1+fy1*(x-x0) print('Значение функции:',ff1) print('Производная:',fy) print('Значение производной:',fy1) print('Касательная:',y) x1=np.arange(x0-1,x0+1,0.01) x11=ff1+fy1*(x1-x0) ff2=ff.subs(x,x1) y1=y.subs(x,x1) #ff3=f(x1) #ff4=ff3.subs(x0,x1) #print(ff4) #for i in x1: #ff5=ff.subs(x,i) #plt.plot(x1,x11,'-r') #plt.plot(x1,ff5) #plt.grid() #plt.show() print(block(f1,sp.pi/4)) x0=np.pi/4 x=Symbol('x') ff=f1(x) ff1=ff.subs(x,x0) fy=sp.diff(ff,x,1) fy1=fy.subs(x,x0) y=ff1+fy1*(x-x0) x1=np.arange(x0-1,x0+1,0.01) xx=np.arange(x0-1,x0+1,0.01) x11=ff1+fy1*(x1-x0) plt.plot(x1,x11,'-r') fff=(np.cos(3*x1))**3 plt.plot(x1,fff,'-g') plt.grid() plt.show() print(block(f1,sp.pi/4)) x0=1 x=Symbol('x') ff=f2(x) ff1=ff.subs(x,x0) fy=sp.diff(ff,x,1) fy1=fy.subs(x,x0) y=ff1+fy1*(x-x0) x1=np.arange(x0-1,x0+1,0.01) xx=np.arange(x0-1,x0+1,0.01) x11=ff1+fy1*(x1-x0) plt.plot(x1,x11,'-r') fff=np.e**(2*x1) plt.plot(x1,fff,'-g') plt.grid() plt.show() print(block(f2,1))

Значение функции: -sqrt(2)/4 Производная: -9*sin(3*x)*cos(3*x)**2 Значение производной: -9*sqrt(2)/4 Касательная: -9*sqrt(2)*(x - pi/4)/4 - sqrt(2)/4 None

Значение функции: -sqrt(2)/4 Производная: -9*sin(3*x)*cos(3*x)**2 Значение производной: -9*sqrt(2)/4 Касательная: -9*sqrt(2)*(x - pi/4)/4 - sqrt(2)/4 None

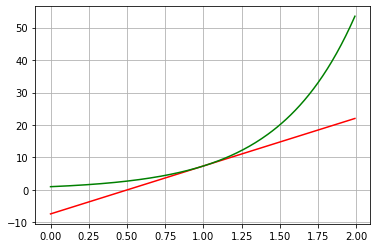
Значение функции: 7.38905609893065 Производная: 2.0*2.71828182845905**(2*x) Значение производной: 14.7781121978613 Касательная: 14.7781121978613*x - 7.38905609893065 None

Упражнение С1

import numpy as np import sympy as sp from sympy import * def f1(x): return (np.sin(1/x))**5 def zn_fc1(f,t,dx): dy1=f(t+dx)-f(t) dy2=f(t-dx)-f(t) d=np.array([dy1/dx, dy1/(-dx)]) return d dx=0.001 x=Symbol('x') print('1.1:',zn_fc1(f1,1,dx)) print('1.2:',zn_fc1(f1,2,dx)) print('1.3:',zn_fc1(f1,-3,dx))

1.1: [-1.35241315 1.35241315] 1.2: [-0.05787592 0.05787592] 1.3: [-0.00602254 0.00602254]

Упражнение С2

import numpy as np import sympy as sp from sympy import * def f1(x): return (sp.sin(1/x))**5 def zn_ffс2(f,t): x=Symbol('x') dx=Symbol('dx') dy=f(x+dx)-f(x) y=sp.limit(dy/dx,dx,0) yy=y.subs(x,t) y1=round(yy,8) return y1 print('1.1:',zn_ffс2(f1,1)) print('1.2:',zn_ffс2(f1,2)) print('1.3:',zn_ffс2(f1,-3))

1.1: -1.35445134 1.2: -0.05795390 1.3: -0.00601679

Упражнение С3

from sympy import * x=Symbol('x') f1=(sp.log(3,x**2+1)/(sp.acos(sp.asin(x)))**3) y1=sp.diff(f1,x,1) yy1=y1.subs(x,0.5) fy=sp.diff(f1,x,1) print(fy) print(yy1)

-2*x*log(3)/((x**2 + 1)*log(x**2 + 1)**2*acos(asin(x))**3) + 3*log(3)/(sqrt(1 - x**2)*sqrt(1 - asin(x)**2)*log(x**2 + 1)*acos(asin(x))**4) 1.69991959748259*log(3)