ЛР7

Пример 1

from scipy import optimize from math import sin , cos, pi def f(x): return (cos(x)-sin(x)) root = optimize.brentq(f, 0, pi/2) print('x =',root) print('f(x) =',f(root))

x = 0.7853981633974484 f(x) = -1.1102230246251565e-16

Пример 2

from scipy import optimize from math import tan def f(x): return (tan(x)) root = optimize.brentq(f, 1, 2) print('x =',root) print('f(x) =',f(root))

x = 1.570796326793586 f(x) = 763027653393.7319

Пример 3

def f(x): return (sin(x)- 1 + x/4) x1 = optimize.brentq(f, 0, 1) print('x1 =',x1) print('f(x1) =',f(x1),'\n') x2 = optimize.brentq(f, 2, 3) print('x2 =',x2) print('f(x2) =',f(x2),'\n') 5 x3 = optimize.brentq(f, 5, 6) print('x3 =',x3) print('f(x3) =',f(x3),'\n')

x1 = 0.89048708074438 f(x1) = 2.7755575615628914e-17 x2 = 2.849968934455141 f(x2) = 6.661338147750939e-16 x3 = 5.8128260902615505 f(x3) = -2.220446049250313e-16

Упражнение 1

import numpy as np import sympy as sp import matplotlib.pyplot as plt from sympy.abc import x from matplotlib import style style.use('ggplot') def f(x): return ((x**2-4)/np.abs(x**2-4)) x1=optimize.brentq(f, 0, 10) print('x1 =',x1) print('f(x1) =',f(x1),'\n') x2=optimize.brentq(f, -10, 0) print('x2 =',x2) print('f(x2) =',f(x2),'\n') y=(x**2-4)/np.abs(x**2-4) sp.plot((y,(x,-10,-2)),(y,(x,-2,2)),(y,(x,2,10)))

x1 = 1.9999999999993179 f(x1) = -1.0 x2 = -1.9999999999993179 f(x2) = -1.0

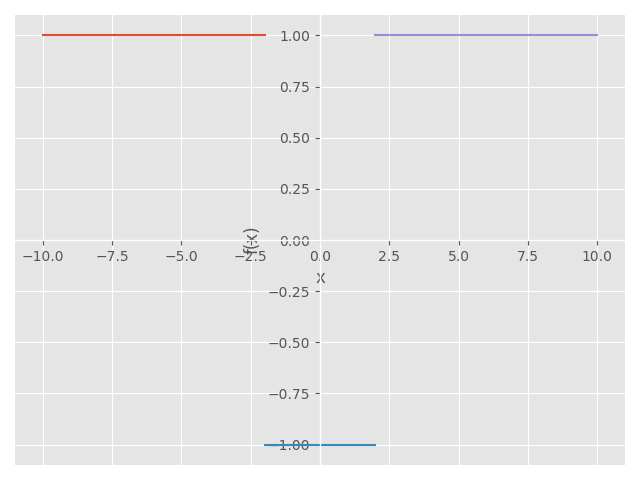
<sympy.plotting.plot.Plot at 0x46a3890>

import numpy as np import sympy as sp import matplotlib.pyplot as plt from sympy.abc import x from matplotlib import style style.use('ggplot') def f(x): return (np.e**(1/(x-2))) y=np.e**(1/(x-2)) sp.plot((y,(x,-5,2)),(y,(x,2,7)),adaptive=False, nb_of_points=20)

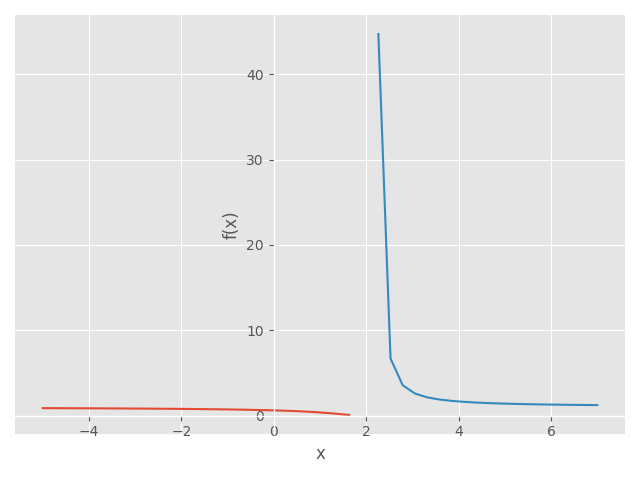
<sympy.plotting.plot.Plot at 0x58ff1c8>

Упражнение 2

import numpy as np import sympy as sp from scipy import optimize import matplotlib.pyplot as plt from sympy.abc import x from matplotlib import style style.use('ggplot') def f(x): return (3+np.sqrt(x)-np.e**(x/2)) x1=optimize.brentq(f, 0, 10) print('x1 =',x1) print('f(x1) =',f(x1),'\n') y=-3-sp.sqrt(x)+np.e**(x/2) sp.plot(y,adaptive=False, nb_of_points=100)

x1 = 3.1235886192561138 f(x1) = 8.881784197001252e-16

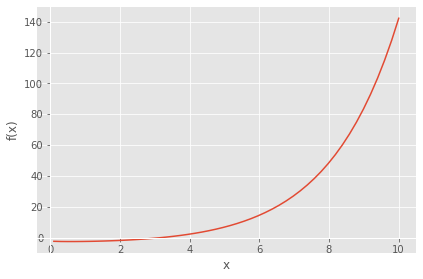
<sympy.plotting.plot.Plot at 0x284bc48bc40>

import numpy as np import sympy as sp import matplotlib.pyplot as plt from sympy.abc import x def f(x): return (x**3-8*x**2+17*x+np.sqrt(x)-10) x1=optimize.brentq(f, 0, 1) print('x1 =',x1) print('f(x1) =',f(x1),'\n') x2=optimize.brentq(f, 1,3) print('x2 =',x2) print('f(x2) =',f(x2),'\n') x4=optimize.brentq(f, 3,6) print('x3 =',x3) print('f(x3) =',f(x3),'\n') y=x**3-8*x**2+17*x+sp.sqrt(x)-10 sp.plot(y,adaptive=False, nb_of_points=100)

x1 = 0.8172611734487208 f(x1) = 1.4210854715202004e-14 x2 = 2.424415309304906 f(x2) = -5.329070518200751e-15 x3 = 2.424415309304906 f(x3) = -5.329070518200751e-15

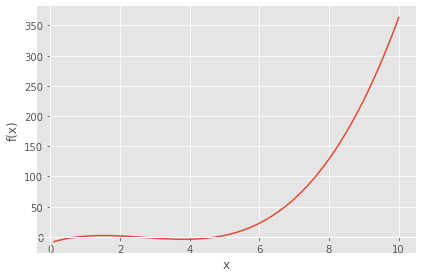
<sympy.plotting.plot.Plot at 0x284bc6660d0>

Пример 4

from sympy.solvers import solve from sympy import Symbol x = Symbol('x') ans=solve(x**4 + x**3 - x - 1, x) print(ans)

[-1, 1, -1/2 - sqrt(3)*I/2, -1/2 + sqrt(3)*I/2]

from sympy.solvers import solve from sympy import Symbol y = Symbol('y') ans=solve(y**2 +y, y) print(ans)

[-1, 0]

Пример 5

from sympy.solvers import solve from sympy import Symbol, cos x = Symbol('x') ans=solve(cos(x), x) ans

[pi/2, 3*pi/2]

Пример 6

from sympy.solvers import nsolve from sympy import Symbol, sin x = Symbol('x') eq = sin(x) - x - 1 a = nsolve(eq, 0) print ('x = ', a) print ('f(x) = ', eq.subs(x,a))

x = -1.93456321075202 f(x) = 0

Упражнени 3

from sympy.solvers import nsolve import numpy as np from sympy import Symbol x = Symbol('x') eq=np.e**(3*x)-(3*x)**(np.e) a=nsolve(eq,0) print ('x = ', a) print ('f(x) = ', eq.subs(x,a)) y=np.e**(3*x)-(3*x)**(np.e) sp.plot(y,adaptive=False, nb_of_points=100)

x = -0.210003079637967 + 0.16060456040024*I f(x) = -0.284818617606917*(-1 + 0.764772405610018*I)**2.71828182845905 + 2.71828182845905**(-0.6300092389139 + 0.48181368120072*I)

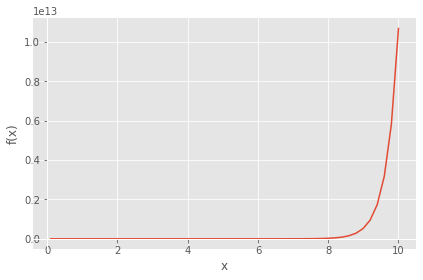
<sympy.plotting.plot.Plot at 0x284c1086c40>

from sympy.solvers import nsolve from math import sin , cos, pi from sympy import Symbol import sympy as sp y = Symbol('x') eq=sp.sin(x)-(x/3) a=nsolve(eq,0) print ('x = ', a) print ('f(x) = ', eq.subs(x,a)) a1=nsolve(eq,-3) print ('x = ', a1) print ('f(x) = ', eq.subs(x,a1)) a2=nsolve(eq,2) print ('x = ', a2) print ('f(x) = ', eq.subs(x,a2)) y=sp.sin(x)-(x/3) sp.plot(y,adaptive=False, nb_of_points=100)

x = 0 f(x) = 0 x = -2.27886266007583 f(x) = 0 x = 2.27886266007583 f(x) = 0

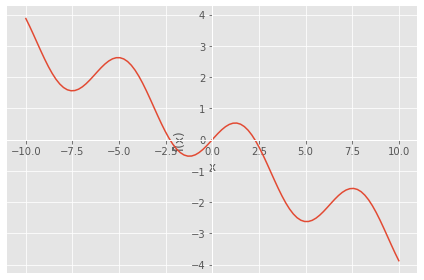
<sympy.plotting.plot.Plot at 0x284bc2df250>

Пример 8

from sympy.solvers import nsolve from sympy import Symbol, sin x = Symbol('x') y = Symbol('y') f1 = x**2 - y - 2 f2 = y-2*x-5 a = nsolve((f1, f2), (x, y), (0, 0)) print('x = ', a) a = nsolve((f1, f2), (x, y), (3, 12)) print('x = ', a)

x = Matrix([[-1.82842712474619], [1.34314575050762]]) x = Matrix([[3.82842712474619], [12.6568542494924]])

Упражнение 4

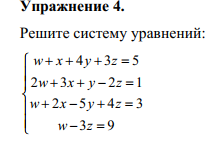
from sympy.solvers import nsolve from sympy import Symbol, sin import matplotlib.pyplot as plt x = Symbol('x') y = Symbol('y') z = Symbol('z') w = Symbol('w') f1=w+x+4*y+z-5 f2=2*w+3*x+y-2*z-1 f3=w+2*x-5*y+4*z-3 f4=w-3*z-9 a = nsolve((f1,f2,f3,f4), (x,y,z,w), (0,0,0,0)) print('x = ', a)

x = Matrix([[-6.83870967741935], [-0.225806451612903], [0.935483870967742], [11.8064516129032]])

Упражнение С1

import numpy as np import sympy as sp from scipy import optimize import matplotlib.pyplot as plt from math import asin from sympy.abc import x from matplotlib import style style.use('ggplot') def f(x): return (np.arcsin(x)/x) x1=optimize.brentq(f, -10, 10) print('x1 =',x1) print('f(x1) =',f(x1),'\n') y=sp.asin(x)/x sp.plot((y,(x,-5,0)),(y,(x,0,5)),adaptive=False, nb_of_points=350)

x1 = 0.0 f(x1) = nan

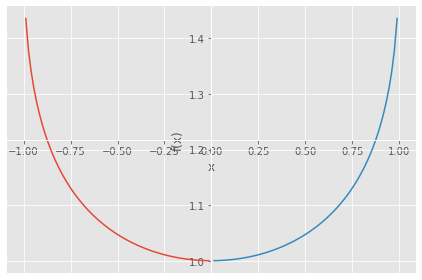
<sympy.plotting.plot.Plot at 0x284bf988310>

import numpy as np import sympy as sp from scipy import optimize import matplotlib.pyplot as plt from math import asin from sympy.abc import x from matplotlib import style style.use('ggplot') def f(x): return (2/(x**2-1)) y=2/(x**2-1) sp.plot((y,(x,-5,-1)),(y,(x,-1,1)),(y,(x,1,5)),adaptive=False, nb_of_points=20)

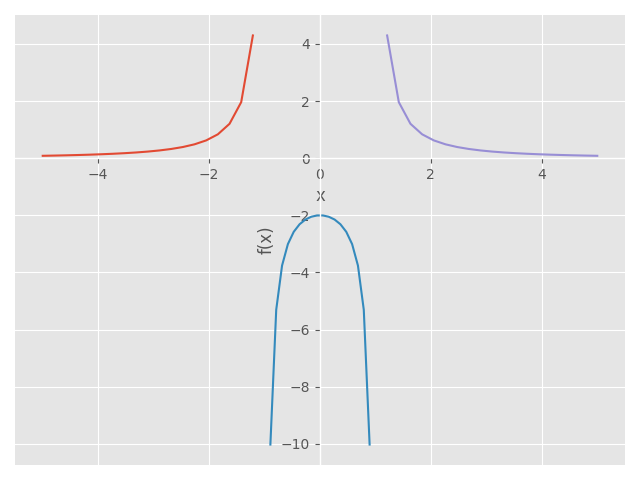
<sympy.plotting.plot.Plot at 0x58a8fe0>

Упражнение С2

import numpy as np import sympy as sp from math import sin, pi import matplotlib.pyplot as plt from sympy.abc import x def f(x): return (x**2-5*x*sin(3*x)+3) x1=optimize.brentq(f, -5, -2.5) print('x1 =',x1) print('f(x1) =',f(x1),'\n') x2=optimize.brentq(f, -2.5, 0) print('x2 =',x2) print('f(x2) =',f(x2),'\n') x3=optimize.brentq(f, 0, 2.5) print('x3 =',x3) print('f(x3) =',f(x3),'\n') x4=optimize.brentq(f, 2.5, 5) print('x4 =',x4) print('f(x4) =',f(x4),'\n') y=(x**2-5*x*sp.sin(3*x)+3) sp.plot(y,adaptive=False, nb_of_points=100)

x1 = -2.843524782667385 f(x1) = -3.552713678800501e-14 x2 = -2.3655901818690075 f(x2) = -3.809397242093837e-12 x3 = 2.3655901818690075 f(x3) = -3.809397242093837e-12 x4 = 2.843524782667385 f(x4) = -3.552713678800501e-14

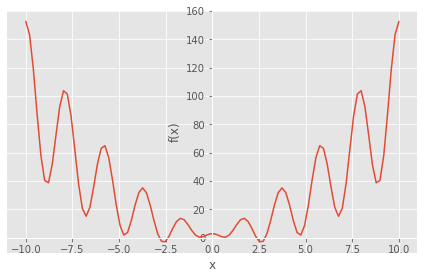
<sympy.plotting.plot.Plot at 0x284bdb79e80>

Упражнение С3

from sympy.solvers import solve from sympy import Symbol x = Symbol('x') ans=solve(x+(1/x)-2) print(ans) y=x+(1/x)-2 sp.plot((y,(x,-10,0)),(y,(x,0,10)),adaptive=False, nb_of_points=100)

[1]

<string>:1: RuntimeWarning: divide by zero encountered in true_divide <string>:1: RuntimeWarning: invalid value encountered in true_divide <string>:1: RuntimeWarning: divide by zero encountered in true_divide <string>:1: RuntimeWarning: invalid value encountered in true_divide

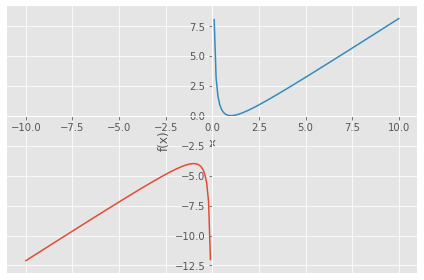
<sympy.plotting.plot.Plot at 0x284bf2d1730>

from sympy.solvers import solve from sympy import Symbol x = Symbol('x') eq=sp.log(1+x)+sp.log(1-x**2) a=nsolve(eq,0) print ('x1 = ', a) print ('f(x1) = ', eq.subs(x,a)) a1=nsolve(eq,0.5) print ('x2 = ', a1) print ('f(x2) = ', eq.subs(x,a1)) y=(sp.log(1+x)+sp.log(1-x**2)) sp.plot(y,adaptive=False, nb_of_points=1000)

x1 = 0 f(x1) = 0 x2 = 0.618033988749895 f(x2) = -5.55111512312578e-17

<sympy.plotting.plot.Plot at 0x284be1951c0>