Лаб. 5 КП ОМА

ЛР5

Пример 1

import sympy as sp x=sp.Symbol('x') %whos

Variable Type Data/Info ------------------------------ sp module <module 'sympy' from '/li<...>kages/sympy/__init__.py'> x Symbol x

Пример 2

import sympy as sp n=3 a=[sp.symbols('a%d'%i) for i in range(n)] sp.pprint(a)

[a₀, a₁, a₂]

import sympy as sp from sympy.abc import x,y,z,alpha,beta sp.pprint(alpha*x**2+2*x*y-3*beta*z-z**2)

2 2 α⋅x - 3⋅β⋅z + 2⋅x⋅y - z

import sympy as sp from sympy.abc import pi sp.pprint(sp.sin(pi)) print(sp.sin(sp.pi))

sin(π) 0

Упражнение 1

import sympy as sp import numpy as np from sympy.abc import pi k=np.arange(1,11) w=[sp.cos((n*sp.pi)/2) for n in k] print("sympy:",w) v=np.cos((k*np.pi)/2) print("numpy:",v)

sympy: [0, -1, 0, 1, 0, -1, 0, 1, 0, -1] numpy: [ 6.1232340e-17 -1.0000000e+00 -1.8369702e-16 1.0000000e+00 3.0616170e-16 -1.0000000e+00 -4.2862638e-16 1.0000000e+00 5.5109106e-16 -1.0000000e+00]

Пример 3

import sympy as sp from sympy.abc import x,y v = sp.sin(sp.pi)**2+sp.cos(sp.pi)**2 sp.pprint(v) print(v) print('\n after simplify='+str(sp.simplify(v)))

1 1 after simplify=1

Упражнени 3

import sympy as sp from sympy.abc import x s=(x**7+3*x**2-4)/(x-1) f=sp.factor(s) print(f) p=sp.simplify(s) print(p)

x**6 + x**5 + x**4 + x**3 + x**2 + 4*x + 4 (x**7 + 3*x**2 - 4)/(x - 1)

Упражнение 4

import sympy as sp from sympy.abc import x,y a=x**4+4 b=x**7+1 c=2*x**3+y*x**2-5*x*y**2+2*y**3 print(sp.factor(a)) print(sp.factor(b)) print(sp.factor(c))

(x**2 - 2*x + 2)*(x**2 + 2*x + 2) (x + 1)*(x**6 - x**5 + x**4 - x**3 + x**2 - x + 1) (x - y)*(x + 2*y)*(2*x - y)

Пример 3.2

import sympy as sp from sympy.abc import x a = sp.solve_univariate_inequality(x**2>=4,x) sp.pprint(a)

(2 ≤ x ∧ x < ∞) ∨ (x ≤ -2 ∧ -∞ < x)

import sympy as sp from sympy.abc import x a = sp.solve_univariate_inequality(x**2>=4,x,relational=False) b = sp.solve_univariate_inequality(x**2<=9,x,relational=False) c = sp.Intersection(a,b) sp.pprint(c)

[-3, -2] ∪ [2, 3]

Пример 4

import sympy as sp from sympy.abc import x m=sp.solve_univariate_inequality(sp.Abs(x**2-3)>3,x,relational=False) sp.N(m,4)

Union(Interval.open(-oo, -2.449), Interval.open(2.449, oo))

Упражнение 5

import sympy as sp from sympy.abc import x j=sp.solve_univariate_inequality(x**3+3*x>3,x,relational=False) sp.N(j,5)

Interval.open(0.81773, oo)

Пример 5

import sympy as sp from sympy.abc import n a = sp.solve_univariate_inequality(sp.Abs(((n**3+3*n+10)/(2*n**3-2*n+5))-0.5)<0.001,n,relational=False) b = sp.solve_univariate_inequality(n>0,n,relational=False) sp.Intersection(a,b)

Interval.open(45.6410785465307, oo)

Упражнение 6

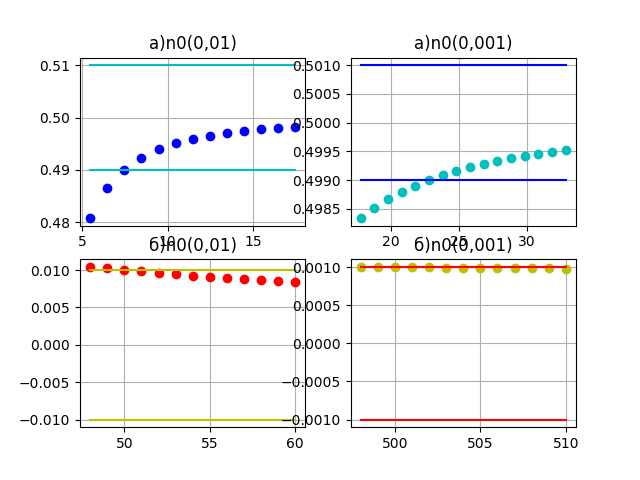
import sympy as sp import numpy as np import matplotlib.pyplot as plt from sympy.abc import n,m e1=0.01 e2=0.001 lim1=sp.limit((n**3-1)/(2*n**3+2*n),n,sp.oo) a1=sp.solve_univariate_inequality(sp.Abs(((n**3-1)/(2*n**3+2*n))-lim1)<e1,n,relational=False) b1=sp.solve_univariate_inequality(n>0,n,relational=False) x1=sp.Intersection(a1,b1) print(x1) a2=sp.solve_univariate_inequality(sp.Abs(((n**3-1)/(2*n**3+2*n))-lim1)<e2,n,relational=False) b2=sp.solve_univariate_inequality(n>0,n,relational=False) x2=sp.Intersection(a2,b2) print(x2) n01=7.46 n1=np.arange(n01-2,n01+11) aa1=(n1**3-1)/(2*n1**3+2*n1) n101=[lim1 - e1 for i in range(len(n1))] n102=[lim1 + e1 for i in range(len(n1))] n02=22.82 n2=np.arange(n02-5,n02+11) aa2=(n2**3-1)/(2*n2**3+2*n2) n201=[lim1 - e2 for i in range(len(n2))] n202=[lim1 + e2 for i in range(len(n2))] lim2=sp.limit((m**3+2*m)/(2*m**4+1),m,sp.oo) c1=sp.solve_univariate_inequality(sp.Abs(((m**3+2*m)/(2*m**4+1))-lim2)<e1,m,relational=False) d1=sp.solve_univariate_inequality(m>0,m,relational=False) y1=sp.Intersection(c1,d1) print(y1) c2=sp.solve_univariate_inequality(sp.Abs(((m**3+2*m)/(2*m**4+1))-lim2)<e2,m,relational=False) d2=sp.solve_univariate_inequality(m>0,m,relational=False) y2=sp.Intersection(c2,d2) print(y2) m01=50 m1=np.arange(m01-2,m01+11) aa3=(m1**3+2*m1)/(2*m1**4+1) m101=[lim2 - e1 for i in range(len(m1))] m102=[lim2 + e1 for i in range(len(m1))] am=0 m02=500 m2=[j for j in range(498, 511)] m201=[lim2 - e2 for j in range(len(m2))] m202=[lim2 + e2 for j in range(len(m2))] plt.subplot(2,2,1) plt.plot(n1,aa1,'ob') plt.plot(n1,n101,'-c') plt.plot(n1,n102,'-c') plt.title('a)n0(0,01)') plt.grid() plt.subplot(2,2,2) plt.plot(n2,aa2,'oc') plt.plot(n2,n201,'-b') plt.plot(n2,n202,'-b') plt.title('a)n0(0,001)') plt.grid() plt.subplot(2,2,3) plt.plot(m1,aa3,'or') plt.plot(m1,m101,'-y') plt.plot(m1,m102,'-y') plt.title('б)n0(0,01)') plt.grid() plt.subplot(2,2,4) for j in range(0, len(m2)): aa4 = (m2[j]**3 + 2*m2[j])/(2*m2[j]**4 + 1) plt.plot(m2[j],aa4,'oy') plt.plot(m2, m201,'-r') plt.plot(m2, m202,'-r') plt.title('б)n0(0,001)') plt.grid() plt.show()

Interval.open(7.46321168040309, oo) Interval.open(22.8233947035835, oo) Union(Interval.open(0, 0.00499993750859309), Interval.open(50.0399321945156, oo)) Union(Interval.open(0, 0.000499999937500086), Interval.open(500.003999932002, oo))

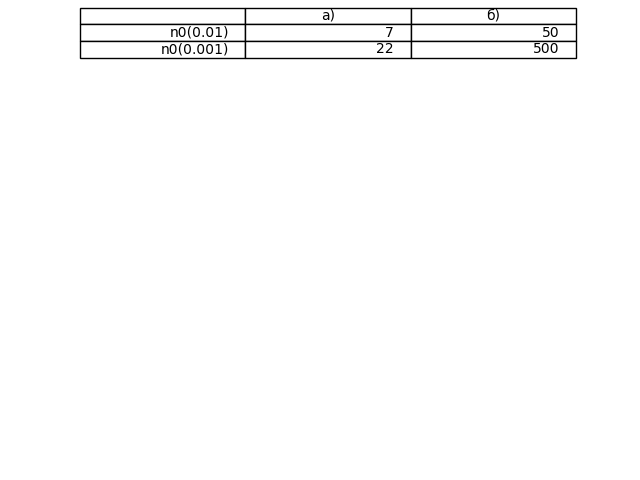
fig, ax = plt.subplots() ax.xaxis.set_visible(False) ax.yaxis.set_visible(False) st1=("", "а)", "б)") st23 = np.array([['n0(0.01)', '7', '50'], ['n0(0.001)', '22', '500']]) plt.table(cellText=st23,colLabels=st1,loc='top') ax.spines['right'].set_visible(False) ax.spines['left'].set_visible(False) ax.spines['top'].set_visible(False) ax.spines['bottom'].set_visible(False) plt.show()

Упражнение C1

import sympy as sp from sympy.abc import x u=sp.solve_univariate_inequality(x**3-3.0*x+1.0>0,x,relational=False) print(sp.pprint(u)) uu=sp.solve_univariate_inequality(x**3-3*x+1>0,x,relational=False) print(sp.pprint(uu))

(-1.87938524157182, 0.347296355333861) ∪ (1.53208888623796, ∞) None

--------------------------------------------------------------------------- ValueError Traceback (most recent call last) File /lib/python3.10/site-packages/sympy/solvers/inequalities.py:530, in solve_univariate_inequality(expr, gen, relational, domain, continuous) 528 if solns is None: 529 # in which case we raise ValueError --> 530 raise ValueError 531 except (ValueError, NotImplementedError): 532 # replace gen with generic x since it's 533 # univariate anyway ValueError: During handling of the above exception, another exception occurred: NotImplementedError Traceback (most recent call last) Cell In [67], line 5 3 u=sp.solve_univariate_inequality(x**3-3.0*x+1.0>0,x,relational=False) 4 print(sp.pprint(u)) ----> 5 uu=sp.solve_univariate_inequality(x**3-3*x+1>0,x,relational=False) 6 print(sp.pprint(uu)) File /lib/python3.10/site-packages/sympy/solvers/inequalities.py:534, in solve_univariate_inequality(expr, gen, relational, domain, continuous) 530 raise ValueError 531 except (ValueError, NotImplementedError): 532 # replace gen with generic x since it's 533 # univariate anyway --> 534 raise NotImplementedError(filldedent(''' 535 The inequality, %s, cannot be solved using 536 solve_univariate_inequality. 537 ''' % expr.subs(gen, Symbol('x')))) 539 expanded_e = expand_mul(e) 540 def valid(x): 541 # this is used to see if gen=x satisfies the 542 # relational by substituting it into the (...) 548 # 549 # expanded_e, expr and gen used from enclosing scope NotImplementedError: The inequality, x**3 - 3*x + 1 > 0, cannot be solved using solve_univariate_inequality.

Упражнение С2

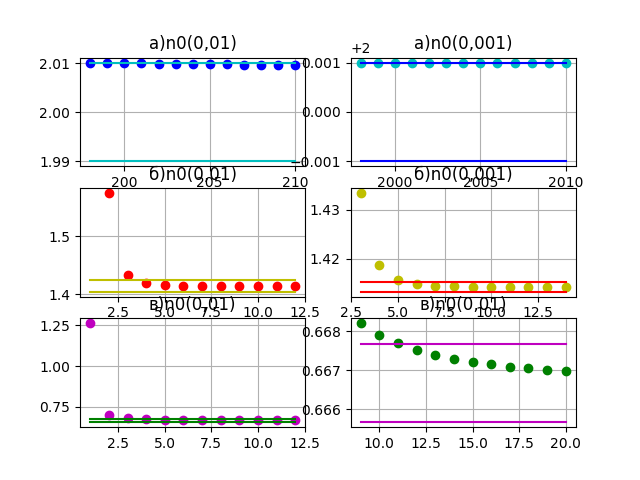
import sympy as sp from sympy import * import matplotlib.pyplot as plt from sympy.abc import n,m,k from scipy.optimize import bisect e1=0.01 e2=0.001 lim1=sp.limit((2*n**5+2*n**4+3)/(n**5-5*n-10000),n,sp.oo) a1=sp.solve_univariate_inequality(sp.Abs(((2*n**5+2*n**4+3)/(n**5-5*n-10000))-lim1)<e1,n,relational=False) b1=sp.solve_univariate_inequality(n>0,n,relational=False) x1=sp.Intersection(a1,b1) print(x1) a2=sp.solve_univariate_inequality(sp.Abs(((2*n**5+2*n**4+3)/(n**5-5*n-10000))-lim1)<e2,n,relational=False) b2=sp.solve_univariate_inequality(n>0,n,relational=False) x2=sp.Intersection(a2,b2) print(x2) n1=[i for i in range(198, 211)] n101=[lim1 - e1 for i in range(len(n1))] n102=[lim1 + e1 for i in range(len(n1))] n2=[j for j in range(1998, 2011)] n201=[lim1 - e2 for j in range(len(n2))] n202=[lim1 + e2 for j in range(len(n2))] lim2=sp.limit((sp.sqrt(2*m**5+3))/(sp.sqrt(m**5-5)),m,sp.oo) c1=sp.solve_univariate_inequality(sp.Abs(((sp.sqrt(2*m**5+3))/(sp.sqrt(m**5-5)))-lim2)<e1,m,relational=False) d1=sp.solve_univariate_inequality(m>0,m,relational=False) y1=sp.Intersection(c1,d1) print(y1) c2=sp.solve_univariate_inequality(sp.Abs(((sp.sqrt(2*m**5+3))/(sp.sqrt(m**5-5)))-lim2)<e2,m,relational=False) d2=sp.solve_univariate_inequality(m>0,m,relational=False) y2=sp.Intersection(c2,d2) print(y2) m1=[s for s in range(1, 13)] m101=[lim2 - e1 for s in range(len(m1))] m102=[lim2 + e1 for s in range(len(m1))] m2=[c for c in range(3, 15)] m201=[lim2 - e2 for c in range(len(m2))] m202=[lim2 + e2 for c in range(len(m2))] lim3=sp.limit((k**3 + k**2)**(1/3) - (k**3 - k**2)**(1/3),k, sp.oo) f1=(k**3 + k**2)**(1/3) - (k**3 - k**2)**(1/3) f11=lambdify([k], Abs(f1-lim3) - e1) gg1=bisect(f11, 0, 100) print(gg1) f22=lambdify([k], Abs(f1-lim3) - e2) gg2=bisect(f22, 0, 100) print(gg2) k1=[t for t in range(1, 13)] k101=[lim3 - e1 for t in range(len(k1))] k102=[lim3 + e1 for t in range(len(k1))] k2=[r for r in range(9, 21)] k201=[lim3 - e2 for r in range(len(k2))] k202=[lim3 + e2 for r in range(len(k2))] plt.subplot(3,2,1) for i in range(0, len(n1)): aa1 = (2*n1[i]**5+2*n1[i]**4+3)/(n1[i]**5-5*n1[i]-10000) plt.plot(n1[i],aa1,'ob') plt.plot(n1,n101,'-c') plt.plot(n1,n102,'-c') plt.title('a)n0(0,01)') plt.grid() plt.subplot(3,2,2) for j in range(0, len(n2)): aa2 = (2*n2[j]**5+2*n2[j]**4+3)/(n2[j]**5-5*n2[j]-10000) plt.plot(n2[j],aa2,'oc') plt.plot(n2,n201,'-b') plt.plot(n2,n202,'-b') plt.title('a)n0(0,001)') plt.grid() plt.subplot(3,2,3) for s in range(0, len(m1)): aa3 = (np.sqrt(2*m1[s]**5+3))/(np.sqrt(m1[s]**5-5)) plt.plot(m1[s],aa3,'or') plt.plot(m1,m101,'-y') plt.plot(m1,m102,'-y') plt.title('б)n0(0,01)') plt.grid() plt.subplot(3,2,4) for c in range(0, len(m2)): aa4 = (np.sqrt(2*m2[c]**5+3))/(np.sqrt(m2[c]**5-5)) plt.plot(m2[c],aa4,'oy') plt.plot(m2, m201,'-r') plt.plot(m2, m202,'-r') plt.title('б)n0(0,001)') plt.grid() plt.subplot(3,2,5) for t in range(0, len(k1)): aa5 = (k1[t]**3 + k1[t]**2)**(1/3) - (k1[t]**3 - k1[t]**2)**(1/3) plt.plot(k1[t],aa5,'om') plt.plot(k1,k101,'-g') plt.plot(k1,k102,'-g') plt.title('в)n0(0,01)') plt.grid() plt.subplot(3,2,6) for r in range(0, len(k2)): aa6 = (k2[r]**3 + k2[r]**2)**(1/3) - (k2[r]**3 - k2[r]**2)**(1/3) plt.plot(k2[r],aa6,'og') plt.plot(k2,k201,'-m') plt.plot(k2,k202,'-m') plt.title('в)n0(0,01)') plt.grid() plt.show()

Interval.open(200.001382025172, oo) Interval.open(2000.00000250166, oo) Interval.open((0.1*sqrt(2) + 13.0005)**(1/5)/(0.000100000000000211 + 0.02*sqrt(2))**(1/5), oo) Interval.open((0.01*sqrt(2) + 13.000005)**(1/5)/(1.00000000013978e-6 + 0.002*sqrt(2))**(1/5), oo) 3.583314941529636 11.133114406767675

fig, ax = plt.subplots() ax.xaxis.set_visible(False) ax.yaxis.set_visible(False) st1=("", "а)", "б)", "в)") st23 = np.array([['n0(0.01)', '200', '3', '3'], ['n0(0.001)', '2000', '5', '11']]) ax.table(cellText=st23,colLabels=st1,loc='top') ax.spines['right'].set_visible(False) ax.spines['left'].set_visible(False) ax.spines['top'].set_visible(False) ax.spines['bottom'].set_visible(False) plt.show()