ЛР4

Пример 1

import numpy as np x=np.array([True,True,False]) print(x) y=np.array([1,1,0],dtype=bool) print(y)

[ True True False] [ True True False]

Пример 2

import numpy as np A=np.array([1,2,3]) B=np.array([-1,2,4]) print(A!=B) print(A<B) x=np.array([[2,3,4],[-1,-1,-1]]) y=np.array([[-2,3,5],[2,3,-7]]) print(x) print(y) print(x>=y) h=np.array([[2,3,-4],[0,-2,3]]) print(h) print(h<0) x=np.array([1,2]) y=np.array([2,4]) z=np.array([2,4,3]) print(np.array_equal(x,y)) print(np.array_equal(y,z)) print(np.array_equal(y,z[:2]))

[ True False True] [False False True] [[ 2 3 4] [-1 -1 -1]] [[-2 3 5] [ 2 3 -7]] [[ True True False] [False False True]] [[ 2 3 -4] [ 0 -2 3]] [[False False True] [False True False]] False False True

Упражнение 1

import matplotlib.pyplot as plt import numpy as np from sympy import * z=256 r=np.abs(z) phi=np.angle(z) k=np.arange(1,9) zroot=r**(1/8)*(np.cos((phi+2.0*np.pi*k)/8)+1j*np.sin((phi+2.0*np.pi*k)/8)) print(zroot) plt.plot(zroot.real, zroot.imag,'or') plt.axvline(x=0,color='k') plt.axhline(y=0,color='k') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.axis('equal') t=np.linspace(0,2*np.pi,100) plt.plot(r**(1/8)*np.cos(t),r**(1/8)*np.sin(t),'--c') plt.grid() plt.show() print("1:",np.less(zroot,0)) print("2:",np.isclose(np.real(zroot),0)) print("3:",np.greater(zroot,np.pi/3))

[ 1.41421356e+00+1.41421356e+00j 1.22464680e-16+2.00000000e+00j -1.41421356e+00+1.41421356e+00j -2.00000000e+00+2.44929360e-16j -1.41421356e+00-1.41421356e+00j -3.67394040e-16-2.00000000e+00j 1.41421356e+00-1.41421356e+00j 2.00000000e+00-4.89858720e-16j]

1: [False False True True True True False False] 2: [False True False False False True False False] 3: [ True False False False False False True True]

Пример 3

import numpy as np x=np.array([0,0,1,1], dtype=bool) y=np.array([0,1,0,1],dtype=bool) t=np.array([1<2,5>3]) print(' x = '+str(x)) print(' y = '+str(y)) print('x and y = '+str(x&y)) print('x or y = '+str(x|y)) print('x xor y = '+str(x^y)) print(' not x = '+str(~x))

x = [False False True True] y = [False True False True] x and y = [False False False True] x or y = [False True True True] x xor y = [False True True False] not x = [ True True False False]

Пример 4

import numpy as np z1=28-4j z2=20+10j print('z1'+str(z1)) print('z2'+str(z2)) print('Both of |z_{1}<29 and |z_{2}|<29-->'+str((np.abs(z1)<29)&(np.abs(z2)<29))) print('Any of |z_{1}>32 or |z_{2}|>32-->'+str((np.abs(z1)>32) | (np.abs(z2)>32)))

z1(28-4j) z2(20+10j) Both of |z_{1}<29 and |z_{2}|<29-->True Any of |z_{1}>32 or |z_{2}|>32-->False

Упражнение 2

import cmath import numpy as np z1=2-3j z2=5+1j f1=np.array([np.pi/3]) f2=np.array([5*np.pi/6]) p1=cmath.phase(z1) p2=cmath.phase(z2) zr1=np.real(z1) zr2=np.real(z2) zi1=np.imag(z1) zi2=np.imag(z2) re=3*zr1+2*zr2 im=zi1-zi2 print("1: "+str((np.greater(p1,f1))&(np.less_equal(p2,f2)))) print("2: "+str((np.less(re,8)|(not(np.isclose(im,2))))))

1: [False] 2: True

Пример 5

import numpy as np A=np.array([1,2,3,4]) print('A '+str(A)) print('A>=2 '+str(A[A>=2])) L=np.array([0,1,1,0],dtype=bool) B=A[L] A[L]=-5 print('B=A(L) '+str(B)) print('A(L)=-5 '+str(A))

A [1 2 3 4] A>=2 [2 3 4] B=A(L) [2 3] A(L)=-5 [ 1 -5 -5 4]

Упражнение 3

import numpy as np k=np.arange(1,9) a=1+3j q=a**k re=np.real(q) im=np.imag(q) print("Re(z)>2: "+str(re[re>2])) print("Im(z)<=Re(z): "+str(im[im<=re]))

Re(z)>2: [ 28. 316. 352.] Im(z)<=Re(z): [-96. -12.]

Упражненеи 4

import numpy as np k=np.arange(1,9) a=abs(3-k*1j) print(a) a[(a>4)&(a<=7)]=0 print(a)

[3.16227766 3.60555128 4.24264069 5. 5.83095189 6.70820393 7.61577311 8.54400375] [3.16227766 3.60555128 0. 0. 0. 0. 7.61577311 8.54400375]

Пример 6

import numpy as np import numpy.random as rng import matplotlib.pyplot as plt x=3-6*rng.rand(10000) y=3-6*rng.rand(10000) z=x+1j*y L=(np.abs(z+1j)>=1.5) plt.plot(x[L],y[L],'.') plt.axis('equal') plt.grid() plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.title('$| z+i | \geq 1.5 $') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()

import numpy as np import numpy.random as rng import matplotlib.pyplot as plt x=3-6*rng.rand(10000) y=3-6*rng.rand(10000) z=x+y*1j L=((np.abs(z-1-1j)>=1)&(np.abs(z-1-1j)<=2)) plt.plot(x[L],y[L],'.') plt.axis('equal') plt.grid() plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.title('$1 \leq | z+i | \leq 2 $') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()

Упражнение С1

import matplotlib.pyplot as plt import numpy as np from sympy import * z=-256 r=np.abs(z) phi=np.angle(z) k=np.arange(1,9) zroot=r**(1/8)*(np.cos((phi+2.0*np.pi*k)/8)+1j*np.sin((phi+2.0*np.pi*k)/8)) print(zroot) plt.plot(zroot.real, zroot.imag,'or') plt.axvline(x=0,color='k') plt.axhline(y=0,color='k') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.axis('equal') t=np.linspace(0,2*np.pi,100) plt.plot(r**(1/8)*np.cos(t),r**(1/8)*np.sin(t),'--c') plt.grid() plt.show() print("1:",np.less(zroot,0)) print("2:",np.isclose(zroot,0)) print("3:",np.greater(zroot,2*np.pi/3))

[ 0.76536686+1.84775907j -0.76536686+1.84775907j -1.84775907+0.76536686j -1.84775907-0.76536686j -0.76536686-1.84775907j 0.76536686-1.84775907j 1.84775907-0.76536686j 1.84775907+0.76536686j]

1: [False True True True True False False False] 2: [False False False False False False False False] 3: [False False False False False False False False]

Упражнение С2

import numpy as np z1=2-3j z2=5+1j m1=abs(z1) m2=abs(z2) print("1: "+str((np.greater_equal(m1,5))&(np.less_equal(m2,6)))) print("2: "+str((np.less(m1,4)|(np.less(m2,4)))))

1: False 2: True

Упражнение С3

import numpy as np k=np.arange(1,9) a=1-3j q=a**k re=np.real(q) im=np.imag(q) print("Re(z)>2: "+str(re[re>2])) print("Im(z)<=Re(z): "+str(im[im<=re]))

Re(z)>2: [ 28. 316. 352.] Im(z)<=Re(z): [ -3. 12. -936.]

Упражнение С4

import numpy as np k=np.arange(1,9) a=abs(2-k*1j) print(a) a[(a>2)&(a<=5)]=0 print(a)

[2.23606798 2.82842712 3.60555128 4.47213595 5.38516481 6.32455532 7.28010989 8.24621125] [0. 0. 0. 0. 5.38516481 6.32455532 7.28010989 8.24621125]

Упражнение С5

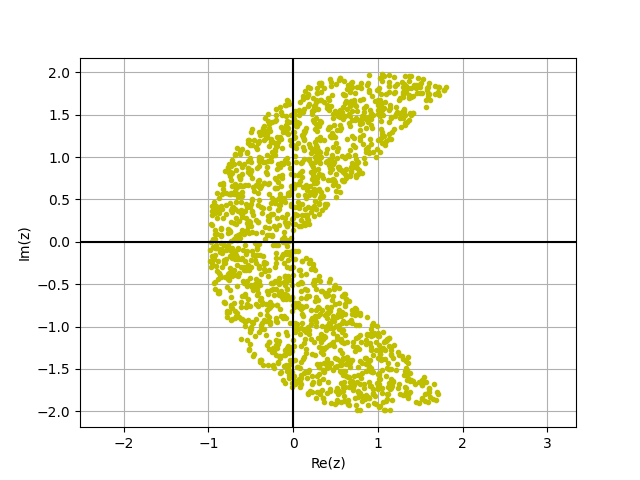
import numpy as np import numpy.random as rng import matplotlib.pyplot as plt x=3-6*rng.rand(10000) y=3-6*rng.rand(10000) z=x+y*1j L=((np.abs(np.angle(z))>=(np.pi/4))&(np.abs(z-1)<=2)) plt.plot(x[L],y[L],'.y') plt.axis('equal') plt.grid() plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()