ЛР3

Пример 1

a=complex(3.5,-2) print(a) b=4+5j print(b)

(3.5-2j) (4+5j)

Пример 2

a=1j print(a**2) z=(3-1j)*(2+4j) print(z) b=z/2j print(b)

(-1+0j) (10+10j) (5-5j)

Упражнение 1

import numpy as np print((2+3j)*(3-1j)) print((1-1j)**3-(1+1j)**3) k=np.arange(1,9) a=1j print(a**k) print(((2-3j)/(1+4j))+((1/(4-1j))))

(9+7j) -4j [ 0.+1.j -1.+0.j -0.-1.j 1.+0.j 0.+1.j -1.+0.j -0.-1.j 1.+0.j] (-0.35294117647058826-0.5882352941176471j)

Пример 3

import numpy as np z=3-7j print(np.conj(z)) print(np.real(z)) print(np.imag(z)) print(np.abs(z)) y=np.array([3+4j, 8-6j]) print(np.abs(y)) z=np.array([1,1j,-1,-1j]) print(np.abs(z)) print(np.angle(z))

(3+7j) 3.0 -7.0 7.615773105863909 [ 5. 10.] [1. 1. 1. 1.] [ 0. 1.57079633 3.14159265 -1.57079633]

Упражнение 2

import numpy as np x=1-np.sqrt(3)*1j y=np.sqrt(3)+1j print(x*(np.conj(y))) print((np.conj(x)/y)**2)

-3.9999999999999996j (0.5000000000000001+0.8660254037844387j)

Упражнение 3

x=(4-5j)*(5-6*(1j**3)) print('x:') print(np.real(x)) print(np.imag(x)) print(np.abs(x)) print(np.angle(x)) print(np.conj(x)) y=(1+1j)**15 print('y:') print(np.real(y)) print(np.imag(y)) print(np.abs(y)) print(np.angle(y)) print(np.conj(y))

x: 50.0 -1.0 50.00999900019995 -0.01999733397315053 (50+1j) y: 128.0 -128.0 181.01933598375618 -0.7853981633974483 (128+128j)

Пример 4.1

import matplotlib.pyplot as plt import numpy as np x=np.array([2+3j, 2-3j, -2+3j, -2-3j]) plt.plot() plt.scatter(np.real(x),np.imag(x), marker="*", color="green", s=30) plt.axis('equal') plt.axvline(x=0,color='k') plt.axhline(y=0, color='k') plt.grid(True) plt.title('Complex numbers') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()

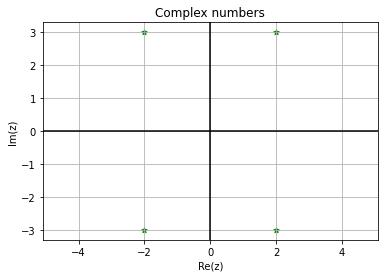
Пример 4.2

import matplotlib.pyplot as plt import numpy as np x=np.array([2+3j, 2-3j, -2+3j, -2-3j]) orig=np.zeros(4) plt.plot() q=plt.quiver(orig,orig,np.real(x),np.imag(x), angles='xy', scale_units='xy', scale=1,color="green") plt.axis([-4,4,-4,4]) plt.axvline(x=0,color='k') plt.axhline(y=0, color='k') plt.grid(True) plt.title('Complex numbers') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()

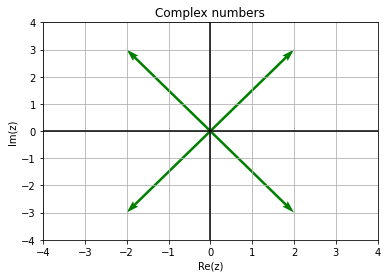
Упражнение 4

import matplotlib.pyplot as plt import numpy as np q=np.array([1+3j]) w=np.array([3+4j]) e=np.array([q+w]) r=np.array([q-w]) o=np.zeros(1) plt.plot() q1=plt.quiver(o,o,np.real(q),np.imag(q), angles='xy', scale_units='xy', scale=1,color="green") w1=plt.quiver(o,o,np.real(w),np.imag(w), angles='xy', scale_units='xy', scale=1,color="red") e1=plt.quiver(o,o,np.real(e),np.imag(e), angles='xy', scale_units='xy', scale=1,color="yellow") r1=plt.quiver(o,o,np.real(r),np.imag(r), angles='xy', scale_units='xy', scale=1,color="blue") plt.axis([-7,7,-7,7]) plt.axvline(x=0,color='k') plt.axhline(y=0, color='k') plt.grid(True) plt.title('Complex numbers') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()

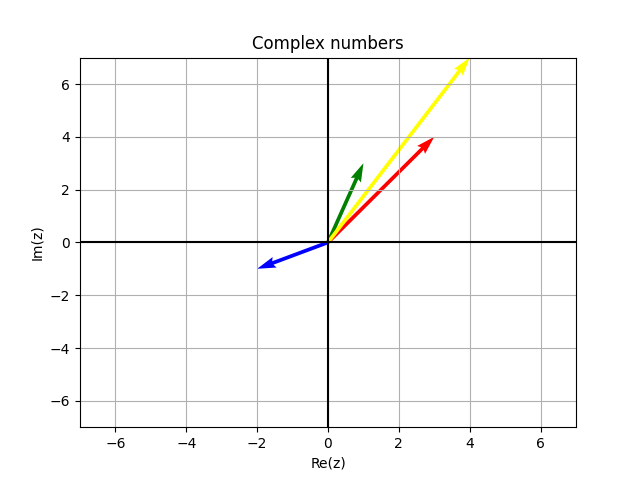
Сумма комплексных чисел: сумма их векторов. Разность: Разность комплексных чисел: разность их векторов

Пример 5

import matplotlib.pyplot as plt import numpy as np z=1+1j r=np.abs(z) phi=np.angle(z) k=np.arange(1,7) zroot=r**(1/6)*(np.cos((phi+2.0*np.pi*k)/6)+1j*np.sin((phi+2.0*np.pi*k)/6)) plt.title('$\sqrt[6]{1+j}$ complex roots') plt.plot(np.real(zroot), np.imag(zroot),'*g') plt.axhline(y=0,color='k') plt.axvline(x=0,color='k') plt.axis('equal') t=np.linspace(0,2*np.pi,100) plt.plot(r**(1/6)*np.cos(t),r**(1/6)*np.sin(t),':') plt.grid(True) plt.show()

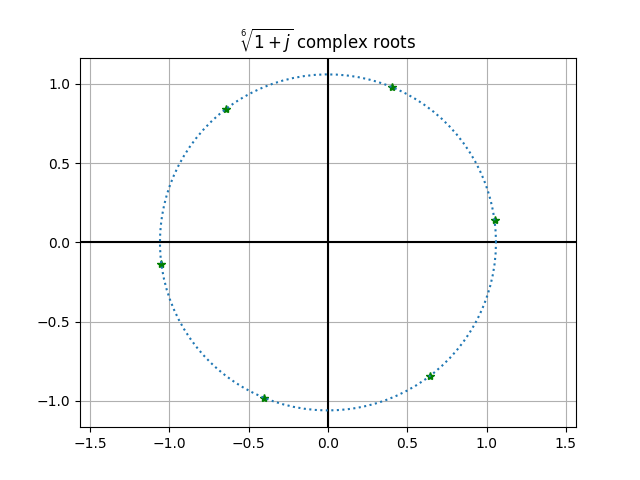
Упражнение 5

import matplotlib.pyplot as plt import numpy as np from sympy import * z=2*np.sqrt(3)-2j r=np.abs(z) phi=np.angle(z) k=np.arange(1,6) zroot=r**(1/5)*(np.cos((phi+2.0*np.pi*k)/4)+1j*np.sin((phi+2.0*np.pi*k)/4)) plt.title('$\sqrt[4]{2\sqrt{3}+2j}$ complex roots') plt.plot(zroot.real, zroot.imag,'*g') plt.axvline(x=0,color='k') plt.axhline(y=0,color='k') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.axis('equal') t=np.linspace(0,2*np.pi,100) plt.plot(r**(1/5)*np.cos(t),r**(1/5)*np.sin(t),'--c') plt.grid(True) plt.plot(np.real(zroot), np.imag(zroot), '-.r') plt.show()

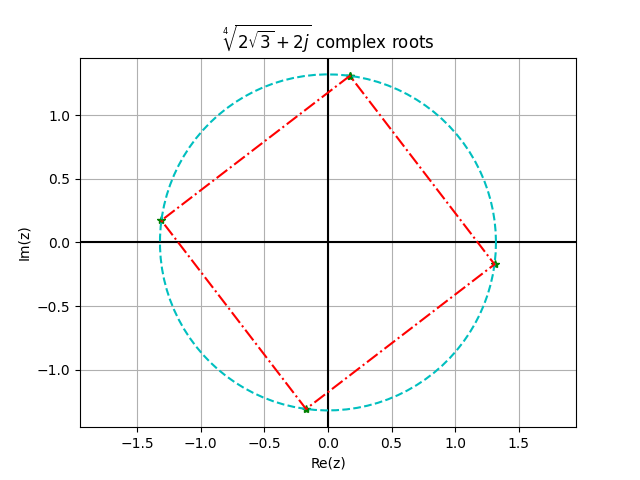
Пример 6

import matplotlib.pyplot as plt import numpy as np r=5 t = np.linspace(0,2*np.pi,100) z = r*(np.cos(t)+1j*np.sin(t)) plt.plot(np.real(z),np.imag(z),'r') plt.grid(True) plt.axis('equal') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.title('|z|='+str(r)) plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()

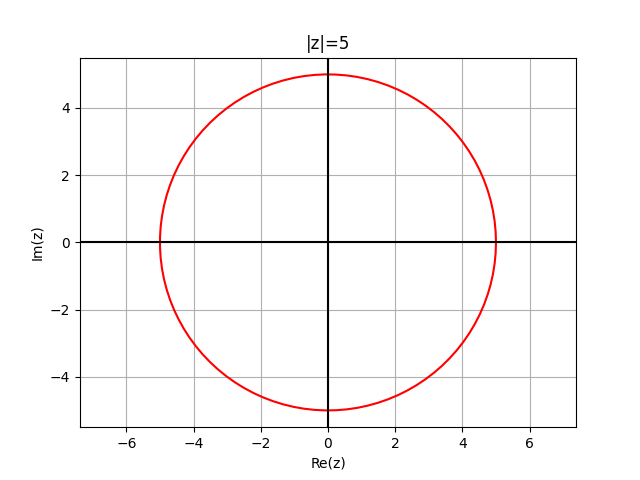
Упражнение 6

import matplotlib.pyplot as plt import numpy as np r1=np.pi/4 r2=5*np.pi/6 t=np.linspace(0,2*np.pi,100) z1=t*(np.cos(r1)+1j*np.sin(r1)) z2=t*(np.cos(r2)+1j*np.sin(r2)) h1,=plt.plot(np.real(z1),np.imag(z1),'r',label='$Arg(z1)=\pi/4$') h2,=plt.plot(np.real(z2),np.imag(z2),'y',label='$Arg(z2)=\5pi/6$') plt.legend(handles=[h1,h2]) plt.grid(True) plt.axis('equal') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()

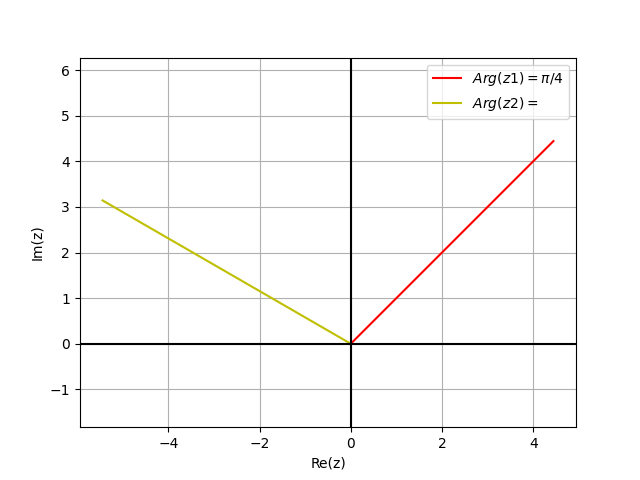
Упражнение С1

print((1-2j)**2*(1-1j)) print((1-1j)**4-(1+1j)**2) print(1j**np.arange(20,41)) print(((2+5j)/(1-3j))+((1/(1-1j))))

(-7-1j) (-4-2j) [ 1.+0.j 0.+1.j -1.+0.j -0.-1.j 1.+0.j 0.+1.j -1.+0.j -0.-1.j 1.+0.j 0.+1.j -1.+0.j -0.-1.j 1.+0.j 0.+1.j -1.+0.j -0.-1.j 1.+0.j 0.+1.j -1.+0.j -0.-1.j 1.+0.j] (-0.7999999999999998+1.5999999999999999j)

Упражнение С2

import numpy as np x=1+np.sqrt(3)*1j y=np.sqrt(3)-1j print(y*(np.conj(x))) print((np.conj(y)/x)**2)

-3.9999999999999996j (0.5000000000000001-0.8660254037844387j)

Упражнение С3

x=(5+4j)*(3-2*(1j**3)) print('x:') print(np.real(x)) print(np.imag(x)) print(np.abs(x)) print(np.angle(x)) print(np.conj(x)) y=(1-1j)**13 print('y:') print(np.real(y)) print(np.imag(y)) print(np.abs(y)) print(np.angle(y)) print(np.conj(y))

x: 7.0 22.0 23.08679276123039 1.2627435457711202 (7-22j) y: -64.0 64.0 90.50966799187809 2.356194490192345 (-64-64j)

Упражнение С4

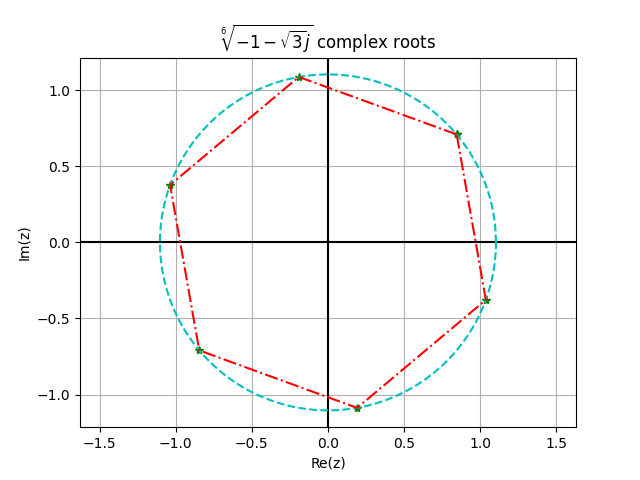
import matplotlib.pyplot as plt import numpy as np from sympy import * z=-1-np.sqrt(3)*1j r=np.abs(z) phi=np.angle(z) k=np.arange(1,8) zroot=r**(1/7)*(np.cos((phi+2.0*np.pi*k)/6)+1j*np.sin((phi+2.0*np.pi*k)/6)) plt.title('$\sqrt[6]{-1-\sqrt{3}j}$ complex roots') plt.plot(zroot.real, zroot.imag,'*g') plt.axvline(x=0,color='k') plt.axhline(y=0,color='k') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.axis('equal') t=np.linspace(0,2*np.pi,100) plt.plot(r**(1/7)*np.cos(t),r**(1/7)*np.sin(t),'--c') plt.grid(True) plt.plot(np.real(zroot), np.imag(zroot), '-.r') plt.show()

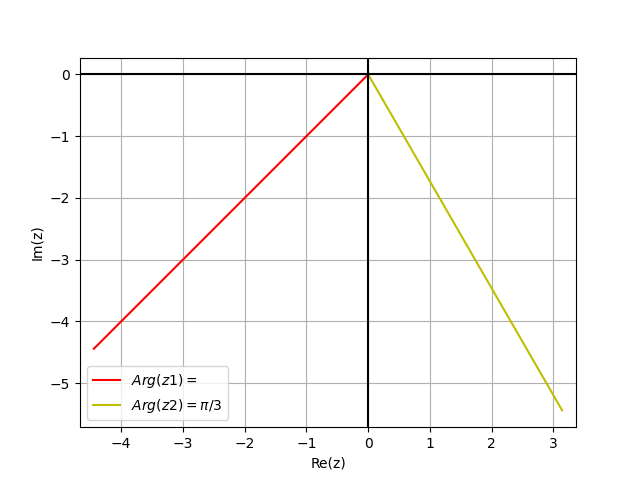
Упражнение C5

import matplotlib.pyplot as plt import numpy as np r1=-3*np.pi/4 r2=-np.pi/3 t=np.linspace(0,2*np.pi,100) z1=t*(np.cos(r1)+1j*np.sin(r1)) z2=t*(np.cos(r2)+1j*np.sin(r2)) h1,=plt.plot(np.real(z1),np.imag(z1),'r',label='$Arg(z1)=\3pi/4$') h2,=plt.plot(np.real(z2),np.imag(z2),'y',label='$Arg(z2)=\pi/3$') plt.legend(handles=[h1,h2]) plt.grid(True) plt.axis('equal') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.xlabel('Re(z)') plt.ylabel('Im(z)') plt.show()