ЛР10

import numpy as np import sympy as sp from sympy import * import matplotlib.pyplot as plt

Пример 1

A = np.array([[1,3],[4,2]]) L,T = np.linalg.eig(A) print(T) D=np.linalg.inv(T).dot(A).dot(T) print(D)

[[-0.70710678 -0.6 ] [ 0.70710678 -0.8 ]] [[-2.00000000e+00 1.11022302e-16] [ 4.44089210e-16 5.00000000e+00]]

AA = Matrix([[1,3],[4,2]]) T,D = AA.diagonalize() print(T) print(D)

Matrix([[-1, 3], [1, 4]]) Matrix([[-2, 0], [0, 5]])

Упражнение 1

a=np.array([[1,-3,1],[3,-3,-1],[3,-5,1]]) aa=Matrix([[1,-3,1],[3,-3,-1],[3,-5,1]]) t=np.linalg.eig(a) d=aa.diagonalize() print(t) print(d)

(array([-1., -2., 2.]), array([[ 0.57735027, -0.42640143, 0.49236596], [ 0.57735027, -0.63960215, 0.12309149], [ 0.57735027, -0.63960215, 0.86164044]])) (Matrix([ [2, 1, 4], [3, 1, 1], [3, 1, 7]]), Matrix([ [-2, 0, 0], [ 0, -1, 0], [ 0, 0, 2]]))

A = np.array([[1,-3,1],[3,-3,-1],[3,-5,1]]) L,T = np.linalg.eig(A) print(T) D=np.linalg.inv(T).dot(A).dot(T) print(D)

[[ 0.57735027 -0.42640143 0.49236596] [ 0.57735027 -0.63960215 0.12309149] [ 0.57735027 -0.63960215 0.86164044]] [[-1.00000000e+00 0.00000000e+00 1.33226763e-15] [ 4.44089210e-16 -2.00000000e+00 8.88178420e-16] [ 6.66133815e-16 -8.88178420e-16 2.00000000e+00]]

t1=np.array([[0.57735027, -0.42640143, 0.49236596],[0.57735027, -0.63960215, 0.12309149],[0.57735027, -0.63960215, 0.86164044]]) d1=np.array([[-1, 0, 0],[ 0, -2, 0],[ 0, 0, 2]]) tt1=np.linalg.inv(t1) aa1=np.dot(t1,d1) #print(np.dot(aa1,tt1)) t=np.array([[2, 1, 4],[3, 1, 1],[3, 1, 7]]) d=np.array([[-2, 0, 0],[ 0, -1, 0],[ 0, 0, 2]]) tt=np.linalg.inv(t) aa=np.dot(t,d) print(np.dot(aa,tt))

[[ 1. -3. 1.] [ 3. -3. -1.] [ 3. -5. 1.]]

Пример 2

A = Matrix([[3,5],[5,3]]) T,D=A.diagonalize() x,y=symbols('x y') f=D[0,0]*x**2+D[1,1]*y**2 f

-2*x**2 + 8*y**2

Упражнение 2

a=Matrix([[6,-2,2],[-2,5,0],[2,0,7]]) t,d=a.diagonalize() x,y,z=symbols('x1 x2 x3') f=d[0,0]*x**2+d[1,1]*y**2+d[2,2]*z**2 f

3*x1**2 + 6*x2**2 + 9*x3**2

Пример 3

x1,y1=symbols('x1 y1') X1=Matrix([[x1,y1]]) X=T/sqrt(2)*X1.T # матрица Т - матрица перехода из примера 2 print('x=',simplify(X[0,0])) print('y=',simplify(X[1,0])) F=3*X[0]**2+10*X[0]*X[1]+3*X[1]**2-32 F=simplify(F/32) F

x= sqrt(2)*(-x1 + y1)/2 y= sqrt(2)*(x1 + y1)/2

-x1**2/16 + y1**2/4 - 1

var('x y') plot_implicit(Eq(3*x**2+10*x*y+3*y**2,32),title='В старой СК', xlabel='x',ylabel='y') plot_implicit(Eq(-x**2.16+y**2.4,1),title='В новой СК', xlabel='x1',ylabel='y1')

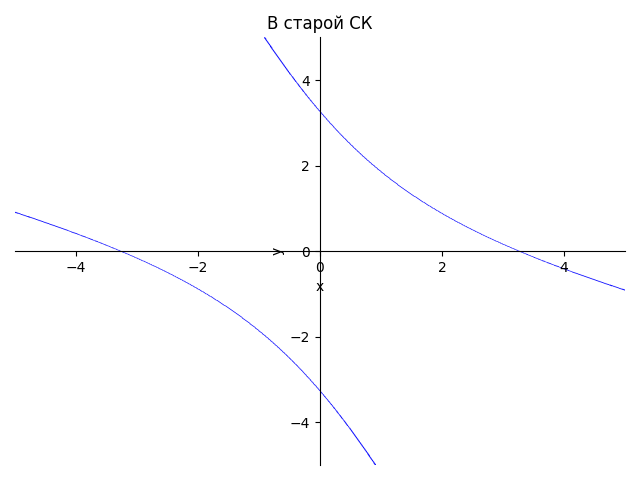
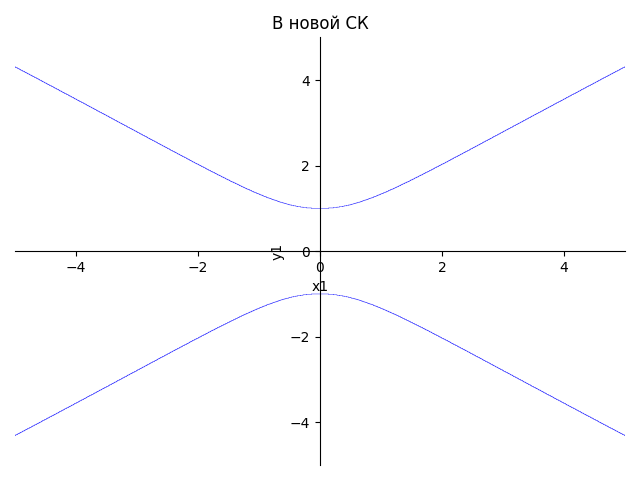
<sympy.plotting.plot.Plot at 0x48a0338>

Упражнение 3

x1,y1=symbols('x1 y1') X1=Matrix([[x1,y1]]) X=T/sqrt(2)*X1.T # матрица Т - матрица перехода из примера 2 print('x=',simplify(X[0,0])) print('y=',simplify(X[1,0])) F=2*X[0]**2-4*X[0]*X[1]+5*X[1]**2+8*X[0]-2*X[1]+9 A=Matrix([[2,-2],[-2,5]]) AA=np.array([[2,-2],[-2,5]]) t,d=A.diagonalize() print("Собственные векторы:",t) print("Собственные числа:",d)

x= sqrt(2)*(-x1 + y1)/2 y= sqrt(2)*(x1 + y1)/2 Собственные векторы: Matrix([[2, -1], [1, 2]]) Собственные числа: Matrix([[1, 0], [0, 6]])

xx1=t[0,0] xx2=t[0,1] xx3=xx1**2+xx2**2 print(xx3) yy1=t[1,0] yy2=t[1,1] yy3=yy1**2+yy2**2 print(y3)

5 5

x1,y1=symbols('x1 y1') x5=((t[0,0]*x1)/np.sqrt(5))+((y1*t[0,1])/np.sqrt(5)) y5=((t[1,0]*x1)/np.sqrt(5))+((y1*t[1,1])/np.sqrt(5)) print(x5) print(y5) xy5=8*x5-2*y5 print(simplify(xy5))

0.894427190999916*x1 - 0.447213595499958*y1 0.447213595499958*x1 + 0.894427190999916*y1 6.26099033699941*x1 - 5.3665631459995*y1

x1,y1=symbols('x1 y1') la1=1 la2=6 k1=14/np.sqrt(5) k2=-12/np.sqrt(5) print(k1) print(k2) f=9 aa=k1/(2*la1) bb=k2/(2*la2) cc=k1**2/(4*la1)+k2**2/(4*la2)-f F2=simplify((la1*(x1+aa)**2+la2*(y1+bb)**2-cc)/2) F2

6.260990336999411 -5.366563145999495

4.9*(0.31943828249997*x1 + 1)**2 + 3*(y1 - 0.447213595499958)**2 - 1.0

var('x y') plot_implicit(Eq(4.9*(0.32*x+1)**2+3*(y-0.45)**2,1),title='В новой СК', xlabel='x1',ylabel='y1')

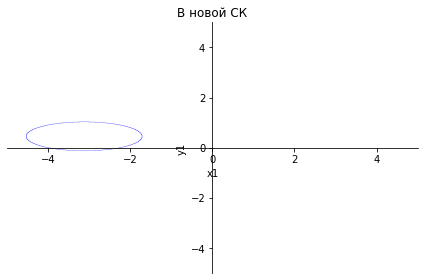
<sympy.plotting.plot.Plot at 0x2391e5ac700>