Лаб. 8 КП АлГем (Кривые второго порядка)

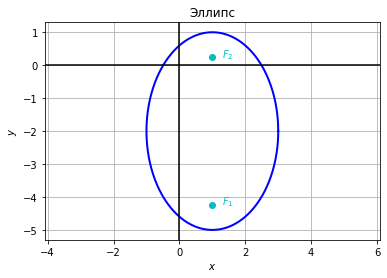
import numpy as np import matplotlib.pyplot as plt a=2 b=3 t=np.arange(0,2*np.pi,0.01) x=a*np.cos(t)+1 y=b*np.sin(t)-2 plt.plot(x,y,lw=2,color='b') plt.xlabel('$x$') plt.ylabel('$y$') plt.axhline(y=0, color='k') plt.axvline(x=0, color='k') plt.plot(1,-np.sqrt(5)-2,'oc') plt.text(1+0.3,-np.sqrt(5)-2,'$F_1$',color='c') plt.plot(1,np.sqrt(5)-2,'oc') plt.text(1+0.3,np.sqrt(5)-2,'$F_2$',color='c') plt.title('Эллипс') plt.axis('equal') plt.grid() plt.show()

from sympy import * e1=Ellipse(Point(1,-2),2,3) e1.foci #координаты фокусов

(Point2D(1, -sqrt(5) - 2), Point2D(1, -2 + sqrt(5)))

e1=Ellipse(Point(1,-2),2,3) e1.area #площадь

6*pi

e1.eccentricity #экцентриситет

sqrt(5)/3

e1.focus_distance #расстояние между фокусами

sqrt(5)

e1.arbitrary_point() #параметрическое уравнение

Point2D(2*cos(t) + 1, 3*sin(t) - 2)

№2

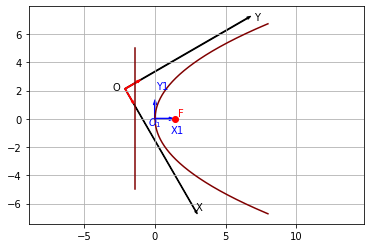
import matplotlib.pyplot as plt import numpy as np from sympy import * import math x1=Symbol('x1') y1=Symbol('y1') al=Symbol('al') x=x1*cos(al)-y1*sin(al) y=y1*cos(al)+x1*sin(al) f=y-2*x y1=solve(f,'y1') y1=x1*(-sin(al) + 2*cos(al))/(2*sin(al) + cos(al)) yy=y1.subs(al,pi/4) x=np.linspace(-1,3,100) al=np.pi/3 x0=1 y0=2 x2=x0*np.cos(-al)-y0*np.sin(-al) y2=y0*np.cos(-al)+x0*np.sin(-al) plt.arrow(0,0,1,0,width=0.08,color='blue') plt.arrow(0,0,0,1,width=0.08,color='blue') x3=np.cos(al) y3=-np.sin(al) x4=np.sin(al) y4=np.cos(al) plt.arrow(0 - 3*np.sqrt(2)/2,0 + 3*np.sqrt(2)/2,10*x3,10*y3,width=0.05,color='black') plt.arrow(0 - 3*np.sqrt(2)/2,0 + 3*np.sqrt(2)/2,10*x4,10*y4,width=0.06,color='black') plt.arrow(0 - 3*np.sqrt(2)/2,0 + 3*np.sqrt(2)/2,1*x3,1*y3,width=0.05,color='red') plt.arrow(0 - 3*np.sqrt(2)/2,0 + 3*np.sqrt(2)/2,1*x4,1*y4,width=0.06,color='red') x = np.arange(0, 8, 0.01) y1 = np.sqrt(4*np.sqrt(2) * x) y2 = -np.sqrt(4*np.sqrt(2) * x) plt.plot(x, y1, color = 'maroon') plt.plot(x, y2, color = 'maroon') plt.plot(np.array([-np.sqrt(2), -np.sqrt(2)]), np.array([-5, 5]), color = 'maroon') plt.plot(np.sqrt(2), 0, 'or') plt.text(np.sqrt(2) + 0.2, 0 + 0.2, 'F',color='red') plt.text(-0.5, -0.5, '$O_1$',color='blue') plt.text(-3, 2, 'O',color='black') plt.text(1 + 0.1,0 - 1, 'X1',color='blue') plt.text(0 + 0.1,2 + 0.1, 'Y1',color='blue') plt.text(2.9, -6.5, 'X') plt.text(7,7, 'Y') plt.axis('equal') plt.grid() plt.show()