Лаб. 6 КП АлГем (Прямая и плоскость)

№1

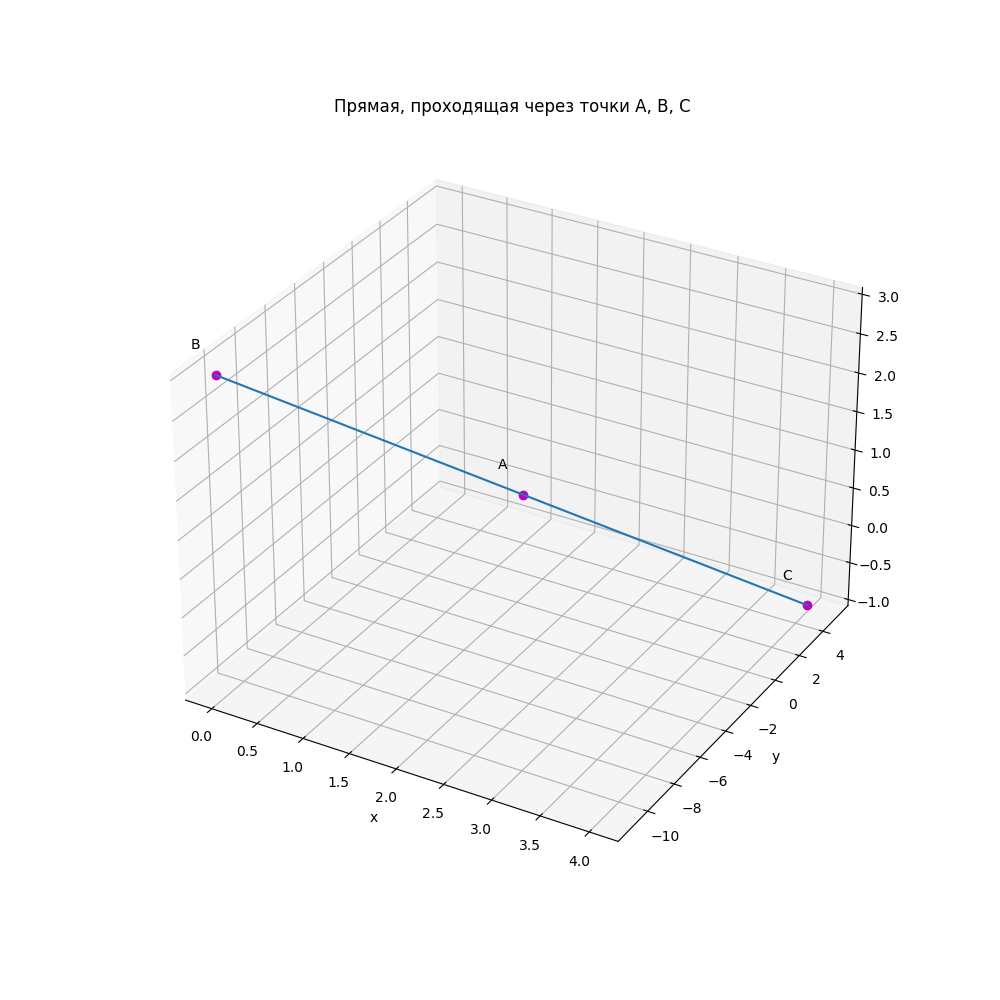
import numpy as np import matplotlib.pyplot as plt import math from sympy import * from matplotlib import cm a=[2,-3,1] b=[0,-11,3] c=[4,5,-1] x=[b[0],c[0]] y=[b[1],c[1]] z=[b[2],c[2]] ab=Line(a,b) ac=Line(a,c) cc=ab.distance(c) if cc==0: print("Расстояние от точки С до прямой АВ равно нулю, соответственно точки А, В, С лежат на одной прямой") ac=Line(a,c) print("Уравнение прямой:",ac.equation()) else: print("Расстояние от точки С до прямой АВ не равно нулю, соответственно точки А, В, С не лежат на одной прямой") fig=plt.figure(figsize=(10,10)) ax=fig.add_subplot(1,1,1,projection='3d') ax.plot(a[0],a[1],a[2],'om') ax.plot(b[0],b[1],b[2],'om') ax.plot(c[0],c[1],c[2],'om') ax.text(a[0]-0.3, a[1]+0.2,a[2]+0.2,'A') ax.text(b[0]-0.3, b[1]+0.2,b[2]+0.2,'B') ax.text(c[0]-0.3, c[1]+0.2,c[2]+0.2,'C') ax.plot(x,y,z) plt.title("Прямая, проходящая через точки A, B, C") plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show()

Расстояние от точки С до прямой АВ равно нулю, соответственно точки А, В, С лежат на одной прямой Уравнение прямой: (-4*x + y + 11, x + z - 3)

№2

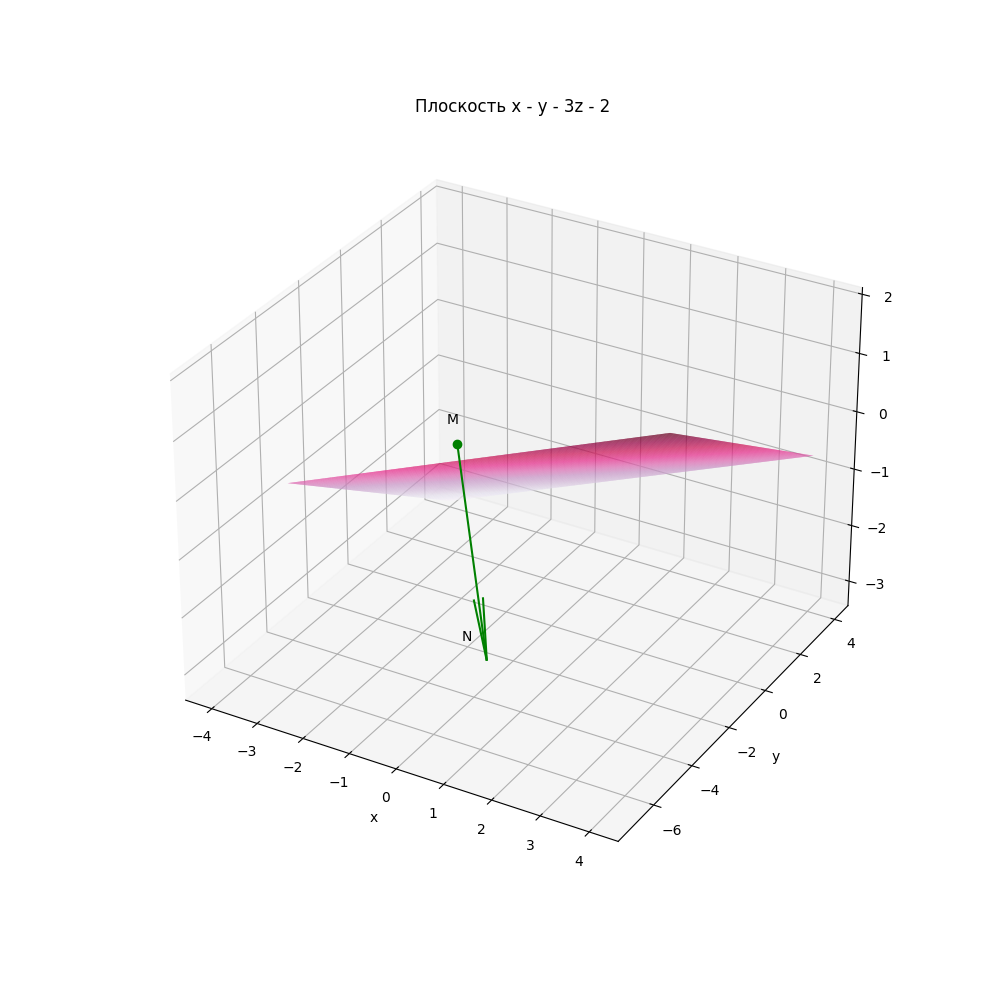
n=[2,-8,-1] mn=[1,-1,-3] m=[n[0]-mn[0],n[1]-mn[1],n[2]-mn[2]] pmn=Plane(m,mn) print("Уравнение плоскости:",pmn.equation()) a=1 b=-1 c=-3 d=-2 f=lambda x,y:(-a*x-b*y-d)/c fig=plt.figure(figsize=(10,10)) ax=fig.add_subplot(1,1,1,projection='3d') xval=np.linspace(-4,4,1000) yval=np.linspace(-4,4,1000) x,y=np.meshgrid(xval,yval) ax.quiver(*m,*mn,color='Green') z=f(x,y) surf=ax.plot_surface(x,y,z,rstride=10,cstride=10,cmap=cm.PuRd) ax.plot(m[0],m[1],m[2],'og') ax.text(m[0]-0.3, m[1]+0.2,m[2]+0.2,'M') ax.text(n[0]-0.5, n[1],n[2]+0.2,'N') plt.title("Плоскость x - y - 3z - 2") plt.xlabel('x') plt.ylabel('y') plt.grid() plt.show()

Уравнение плоскости: x - y - 3*z - 2

№3

a=Plane(Point(0,0,1),(2,3,-4)) b=Plane(Point(0,0,3),(5,-2,1)) print("Угол между плоскостями:",a.angle_between(b)) a1=2 b1=3 c1=-4 d1=4 a2=5 b2=-2 c2=1 d2=-3 f1=lambda x,y:(-a1*x-b1*y-d1)/c1 f2=lambda x,y:(-a2*x-b2*y-d2)/c2 fig=plt.figure(figsize=(10,10)) ax=fig.add_subplot(1,1,1,projection='3d') xval=np.linspace(-4,4,1000) yval=np.linspace(-4,4,1000) x,y=np.meshgrid(xval,yval) z1=f1(x,y) surf=ax.plot_surface(x,y,z1,rstride=10,cstride=10, cmap=cm.gist_heat).set_alpha(0.8) z2=f2(x,y) surf=ax.plot_surface(x,y,z2,rstride=10,cstride=10, cmap=cm.bone).set_alpha(0.5) plt.xlabel('x') plt.ylabel('y') plt.title('Плоскости: 2x +3y − 4z + 4 = 0 и 5x − 2y + z −3 = 0') plt.grid() plt.show()

Угол между плоскостями: pi/2

№4

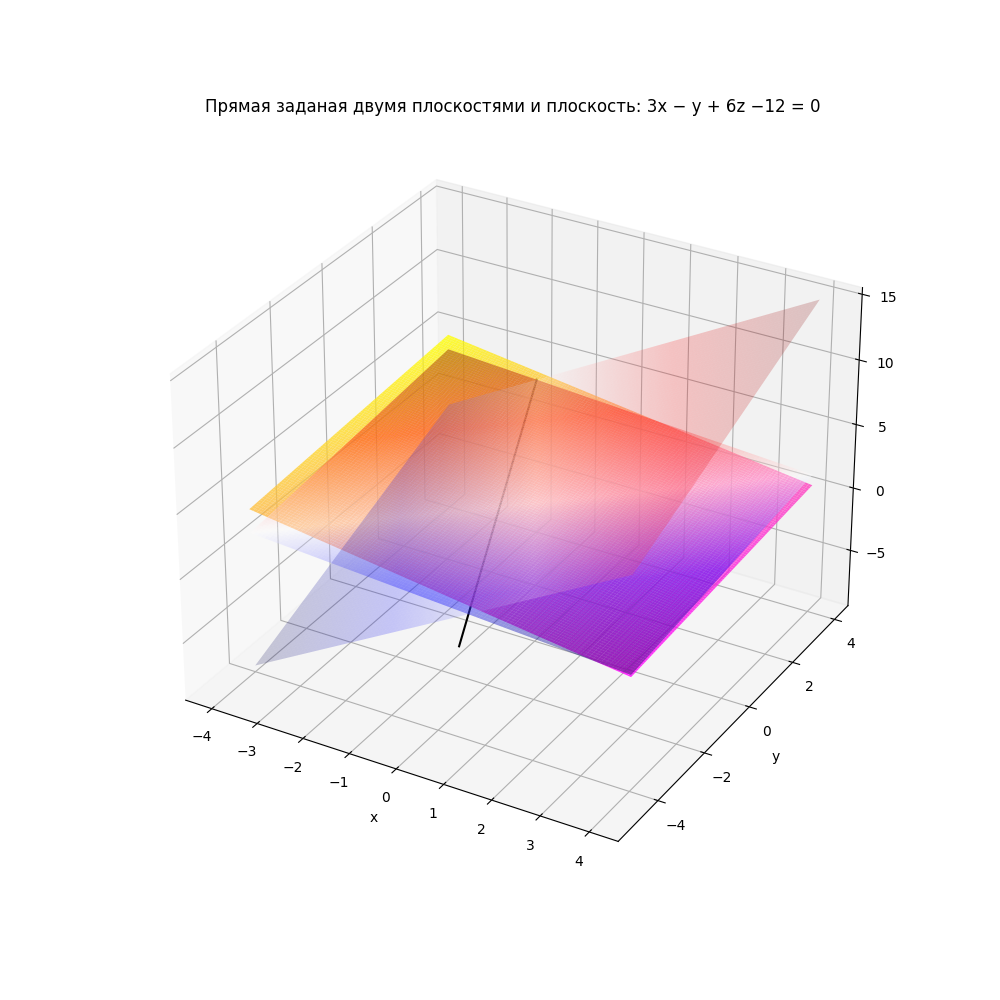
A1=1 B1=-1 C1=4 D1=-6 A2=2 B2=1 C2=-1 D2=3 f1=lambda x,y:(-A1*x-B1*y-D1)/C1 f2=lambda x,y:(-A2*x-B2*y-D2)/C2 fig=plt.figure(figsize=(10,10)) ax=fig.add_subplot(1,1,1,projection='3d') xval=np.linspace(-4,4,1000) yval=np.linspace(-4,4,1000) x,y=np.meshgrid(xval,yval) z1=f1(x,y) surf=ax.plot_surface(x,y,z1,rstride=10,cstride=10, cmap=cm.seismic).set_alpha(0.4) z2=f2(x,y) surf=ax.plot_surface(x,y,z2,rstride=10,cstride=10, cmap=cm.seismic).set_alpha(0.2) t=Point3D(1,-5,0) r=Point3D(-2,4,3) tr=Line3D(t,r) al=Plane((0,0,2),(3,-1,6)) w=al.angle_between(tr) print("Угол между прямой и плоскостью:",w) if w==0: print("Прямая принадлежит плоскости") else: print("Точка пересечения прямой с плоскостью:",al.inersection(tr)) i=[t[0],r[0]] j=[t[1],r[1]] k=[t[2],r[2]] a3=3 b3=-1 c3=6 d3=-12 f3=lambda x,y:(-a3*x-b3*y-d3)/c3 z3=f3(x,y) surf=ax.plot_surface(x,y,z3,rstride=10,cstride=10, cmap=cm.spring).set_alpha(0.8) ax.plot(i,j,k,color='Black') plt.xlabel('x') plt.ylabel('y') plt.title('Прямая заданая двумя плоскостями и плоскость: 3x − y + 6z −12 = 0') plt.grid() plt.show()

Угол между прямой и плоскостью: 0 Прямая принадлежит плоскости