ЛР 3

import numpy as np import matplotlib.pyplot as plt import math from sympy import *

Пример 1

OA=np.array([-2,0]) OB=np.array([1,2]) OC=np.array([1,-1]) print('Векторы имеют координаты:') AB=OB-OA BC=OC-OB AC=OC-OA print('AB:',AB) print('BC:',BC) print('AC:',AC) plt.grid() plt.ylim(-2,3) plt.xlim(-3,2) plt.arrow(-2,0,AB[0],AB[1],width=0.07,length_includes_head=True, facecolor='Yellow') plt.arrow(1,2,BC[0],BC[1],width=0.07,length_includes_head=True,facecolor='Red') plt.arrow(-2,0,AC[0],AC[1],width=0.07,length_includes_head=True,facecolor='Blue') plt.show()

Векторы имеют координаты: AB: [3 2] BC: [ 0 -3] AC: [ 3 -1]

Упражнение 3.1

OA=np.array([-2,0]) OB=np.array([1,2]) OC=np.array([1,-1]) AB=OB-OA BC=OC-OB OD=OC-AB print(OD) CD=OD-OC DA=OA-OD plt.grid() plt.ylim(-5,5) plt.xlim(-5,5) plt.arrow(-2,0,AB[0],AB[1],width=0.07,length_includes_head=True, facecolor='Yellow') plt.arrow(1,2,BC[0],BC[1],width=0.07,length_includes_head=True,facecolor='Red') plt.arrow(1,-1,CD[0],CD[1],width=0.07,length_includes_head=True,facecolor='Blue') plt.arrow(-2,-3,DA[0],DA[1],width=0.07,length_includes_head=True,facecolor='Green') plt.show()

[-2 -3]

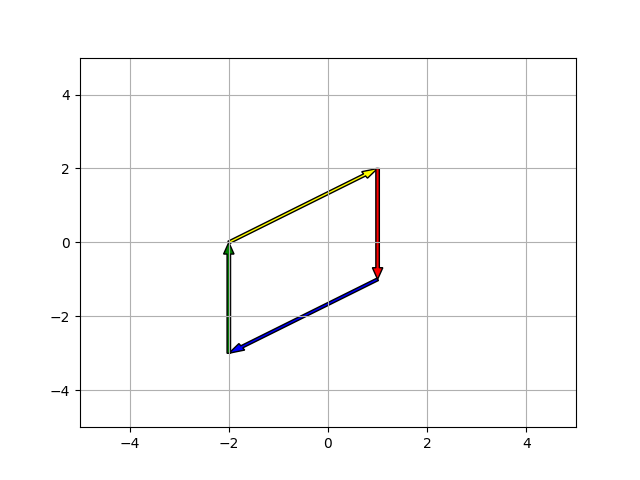
Находится коордтнаты вершины D, после чего строится параллелограм

Упражнение 3.2

x=plt.axes(projection='3d') z=np.array([0,0,0]) a=np.array([1,-2,0]) b=np.array([0,1,1]) c=np.array([1,2,2]) abc=np.matrix('1 -2 0; 0 1 1; 1 2 2') det=np.linalg.det(abc) if det!=0: plt.grid() x.set_ylim([-2,2]) x.set_xlim([-2,2]) x.set_zlim([-2,2]) x.quiver(*z,*a,color='Green') x.quiver(*z,*b,color='Red') x.quiver(*z,*c,color='Blue') x.axis() plt.show() else: print("Векторы не образуют базис")

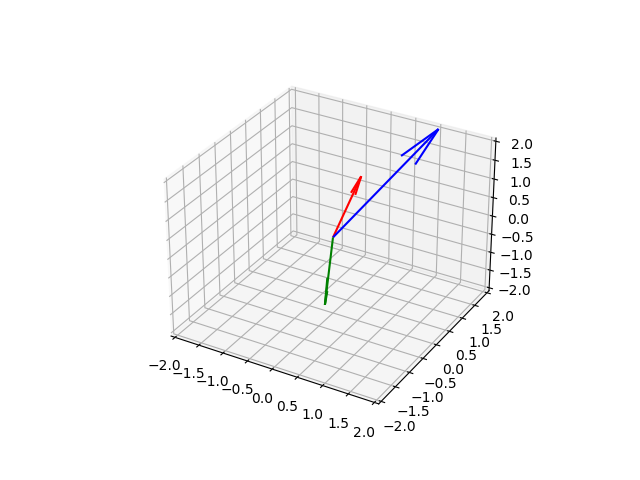
Доказательство образования базиса данными векторами через нахождение определителя и изображение данных векторов

Упражнение 3.3

p,q,r=symbols('p q r') m=np.matrix('1 1 0; -1 1 1; 1 0 -1') s=np.matrix('1; 1; 1') dm=np.linalg.det(m) if dm!=0: print("Векторы линейно независимы") xm=np.matrix(m) xm[:,0]=s ym=np.matrix(m) ym[:,1]=s zm=np.matrix(m) zm[:,2]=s x=round(np.linalg.det(xm)/dm) y=round(np.linalg.det(ym)/dm) z=round(np.linalg.det(zm)/dm) ss=x*p+y*q+z*r print(ss) else: print("Векторы линейно зависимы")

Векторы линейно независимы -p + 2*q - 2*r

Определенеие линейной зависимости векторов и разложение одного вектора через другие

Пример 2

a=np.array([0,5,-1]) b=np.array([-4,9,3]) print ('Вектор a:', a) print ('Вектор b:', b) cos_angle=np.dot(a,b)/np.linalg.norm(a)/np.linalg.norm(b) print ('Косинус угла между a и b:', cos_angle) alfa=np.arccos(cos_angle) alfa=math.degrees(alfa) print ('Угол в градусах:', alfa)

Вектор a: [ 0 5 -1] Вектор b: [-4 9 3] Косинус угла между a и b: 0.8000362836474323 Угол в градусах: 36.86643267303998

Упражнение 3.4

a=np.array([-2,0]) b=np.array([3,4]) c=np.array([4,-1]) ab=b-a bc=c-b ca=a-c ba=a-b cb=b-c ac=c-a caabc=np.dot(ba,bc)/np.linalg.norm(ba)/np.linalg.norm(bc) cabca=np.dot(cb,ca)/np.linalg.norm(cb)/np.linalg.norm(ca) cacab=np.dot(ab,ac)/np.linalg.norm(ab)/np.linalg.norm(ac) q=math.degrees(np.arccos(caabc)) w=math.degrees(np.arccos(cabca)) e=math.degrees(np.arccos(cacab)) print(q) print(w) print(e) print(q+w+e) plt.grid() plt.ylim(-2,5) plt.xlim(-3,5) plt.arrow(-2,0,ab[0],ab[1],width=0.07,length_includes_head=True,facecolor='Yellow') plt.arrow(3,4,bc[0],bc[1],width=0.07,length_includes_head=True,facecolor='Red') plt.arrow(4,-1,ca[0],ca[1],width=0.07,length_includes_head=True,facecolor='Orange') plt.show()

62.65012421993012 69.22774531795417 48.1221304621157 180.0

Находятся вектора и величины углов между ними

Упражнение 3.5

a = np.array([1, 2, 0]) b = np.array([2, 1, 0]) print(np.cross(a, b))

[ 0 0 -3]

Векторное произведение

Пример 3

ax = plt.axes(projection='3d') z = np.array([0, 0, 0]) a = np.array([1, 2, 0]) b = np.array([2, 1, 0]) c = np.cross(a, b) ax.set_xlim([-2, 2]) ax.set_ylim([-2, 2]) ax.set_zlim([-2, 2]) ax.quiver(*z, *a, color='Blue') ax.quiver(*z, *b, color='Green') ax.quiver(*z, *c, color='Red') ax.axis() plt.grid() plt.show()

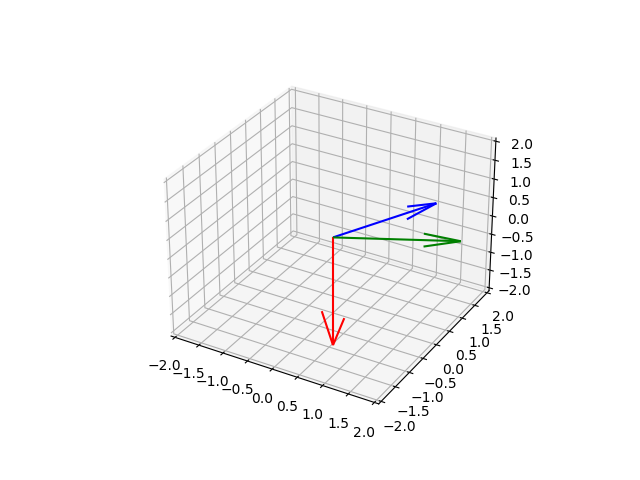
Упражнение 3.6

a=np.array([1,3,-1]) b=np.array([2,-1,4]) c=np.array([5,0,3]) ab=b-a ac=c-a z=np.cross(ab,ac) e=np.matrix(z**2) w=np.sqrt(e[0,0]+e[0,1]+e[0,2]) S=0.5*w print(S)

10.319883720275147

Находятся вектора по координатам точек, затем векторное произведение этих векторов, после длину этого произведения. В конце длина делилтся пополам, получается площадь

Упражнение С1

a=np.matrix('3 -3 0; 4 0 2; 0 1 5') ab=np.matrix([3,4,0]) ac=np.matrix([-3,0,1]) ad=np.matrix([0,2,5]) q=np.cross(ab,ac)*np.transpose(ad) da=np.linalg.det(a) V=(1/6)*da print(V) print(q/6)

9.0 [[9.]]

Находится смешанное произведение векторов и делится на 6