ГУАП

КАФЕДРА 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, к.т.н. доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

Изучение методов фильтрации аудиосигналов в MATLAB. Применение рекурсивных фильтров

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

1. Цель.

Получить навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров.

2. Краткие теоретические сведения о задачах обработки мультимедиа аудиоконтента.

Фильтрацию можно производить без вычисления спектра обрабатываемого оцифрованного аудиосигнала, непосредственно во временной области. В частности, уравнение работы рекурсивного цифрового фильтра имеет вид, которое представлено на рисунке 1.

Рисунок 1 – Формула 1

из которого видно, что формирование массива отсчетов выходного сигнала происходит последовательно. Два массива коэффициентов фильтра ({ar} и {bv}) полностью определяют характеристики фильтра. Заметим, что в системе MATLAB индексация элементов массивов ведется не с нуля, а с единицы, что требует выполнения элементарной модификации всех формул из учебных пособий по обработке сигналов и фильтрации. Впрочем, обычно все стандартные задачи обработки сигналов в MATLAB можно решить вызовом стандартных функций, которые не предполагают поэлементную работы с массивами. Основная задача расчета рекурсивного фильтра заключается в выборе так называемого аналогового фильтра-прототипа некоторого порядка, и вычислении коэффициентов {ar} и {bv} по заданным частотным характеристикам фильтра. Для расчета фильтров существуют разные методы, наиболее простым из которых является метод обобщенного билинейного преобразования передаточной функции аналогового фильтра-прототипа, который и реализован в соответствующих стандартных функциях Matlab.

3. Вариант задания

Вариант задания представлен на рисунке 2. Получается, что нужно реализовать фильтр высоких частот, ограниченных до 800 Гц.

Рисунок 2 – Вариант задания

4. Ход работы

Используется аудиосигнал, который можно прослушать по ссылке: https://disk.yandex.ru/d/onKOeQVtocNuIg [2].

Далее необходимо провести фильтрацию звука, аналогичную той, которая была проведена в Лабораторной работе №2, но уже с применением рекурсивных цифровых функций. Мной, для работы, была выбрана функций butter (для фильтра семейства Баттерворта). Проведение фильтрации и визуализация аудиосигнала, его амплитудного спектра, АЧХ фильтра представлено в Листинге 1.

Листинг 1 – Код для фильтрации и визуализации сигнала

clc, clear, close all %очистка памяти

[input_signal,Fd] = audioread('song1.wav');

N = length(input_signal);%Получить длину данных аудиофайла

IIR_Ord=3; % задаем порядок фильтра-прототипа

% задаем граничные частоты полосы пропускания фильтра

low_freq = 800;

% выполняем расчет коэффициентов РЦФ Баттерворта,

% вызывая стандартную функцию butter(...)

[b a]=butter(IIR_Ord, 2.*low_freq./Fd,'high');

% осуществляем фильтрацию всей имеющейся записи,

% вызывая стандартную функцию Matlab

output_signal(:,1)=filter(b,a,input_signal(:,1));

output_signal(:,2)=filter(b,a,input_signal(:,2));

% вычисляем спектры входного и выходного сигнала

% только для того, чтобы посмотреть графики изменений,

% внесенных фильтром:

Spectr_input=fft(input_signal(:,1));

Spectr_output=fft(output_signal(:,1));

% строим графики спектров входного и выходного сигналов

figure(1)

X=20*log10(abs(Spectr_input)); %Преобразовать в дБ

f=[0:(Fd/N):Fd/2]; %Перевести Абсциссу в Гц

X=X(1:length(f));

semilogx(f,X);

grid;

xlabel('Частота (Гц)');

ylabel('Уровень (дБ)');

title('Амплитудные спектры аудиофайлов');

hold on

Y=20*log10(abs(Spectr_output)); %Преобразовать в дБ

Y=Y(1:length(f));

hLine(2)=semilogx(f,Y);

figure(1)

hold off

legend('input audio','output audio')

% строим график АЧХ фильтра

[H, F] = freqz(b,a, N,'whole',Fd);

f=[0:(Fd/N):Fd/2];

W=H(1:length(f));

figure(2), semilogx(f, 20*log(abs(W))./log(10)), grid

ylim([-110 10])

xlim([1 22000])

% осуществляем построение графиков

% входного и выходного сигналов

figure(3)

subplot(2,1,1); plot(input_signal);

subplot(2,1,2); plot(output_signal);

audiowrite('song1_filtered.wav', output_signal, Fd)

Обработанную запись можно прослушать по ссылке: https://disk.yandex.ru/d/iqUreYyZU0a2mw [3]. Прослушав запись сразу чувствуется, что звук стал тише, в нём меньше басов.

На рисунке 3 можно отчётливо увидеть, что звук после обработки стал более подавленным и менее громким.

Рисунок 3 – Графики каналов до и после обработки

По рисунку 4 можно увидеть, что амплитудный спектр успешно подавлен, что показывает корректную работу фильтра высоких частот с помощью рекурсивной функции.

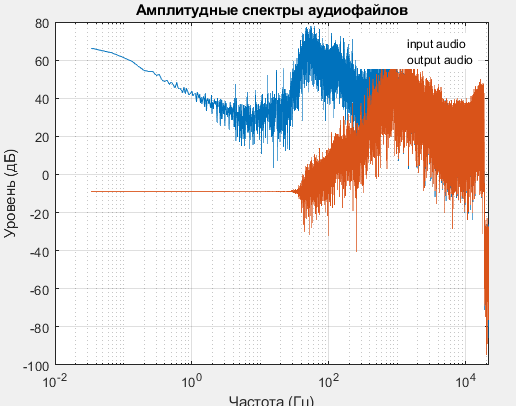
Рисунок 4 – Амплитудный спектр исходного сигнала

Рисунок 5 – График АЧХ фильтра при пропускании сигнала

Вывод

В ходе данной лабораторной работы мы получили навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров, а также изучить концепцию формирующего фильтра для создания шумовых эффектов.

Проведенный сравнительный анализ показал, что в ходе работы мы получили результаты достаточно похожие на те которых мы добились в первой лабораторной работе, так же это подтверждает приведенные в работе графики сигналов. Также стоит отметить, что реализованный в данной работе фильтр имеет менее заметное влияние на изменение аудиосигнала, что вырежется в более слабом изменении звука при оценке на слух.

Список используемой литературы

1. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №3 по дисциплине “Мультимедиа-технологии” гр.4016, 4017. ГУАП, 2024. – 6 с.

2. Яндекс диск. Исходный звук. // URL: https://disk.yandex.ru/d/onKOeQVtocNuIg

3. Яндекс диск. Обработанный звук. // URL: https://disk.yandex.ru/d/iqUreYyZU0a2mw