ГУАП

КАФЕДРА 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, к.т.н. доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

Изучение методов фильтрации аудиосигналов в MATLAB. Применение метода фурье-фильтрации

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

1. Цель.

Изучить основы обработки аудиосигналов на примере метода фильтрации сигналов в спектральном пространстве.

2. Краткие теоретические сведения о задачах обработки мультимедиа аудиоконтента.

Для получения информации о частотном составе любых сигналов в дискретном времени существует специальный метод и алгоритм – быстрое преобразование Фурье (БПФ). В результате его применения к массиву {xn}, который представляет собой, например, последовательность оцифрованных значений звука, образуется массив значений спектра {Xn}. Значения спектра являются комплексными числами, а модуль каждого из них пропорционален амплитуде гармонического компонента, содержащегося в обрабатываемой записи аудисосигнала. Связь целочисленного индекса элементов массива {Xn} с частотой дается формулой:

n=f∙N∙TД,

где TД – период дискретизации сигнала.

Существует также и алгоритм обратного действия (обратное БПФ): по массиву значений спектра {Xn} можно вычислить массив значений сигнала {xn} (иногда говорят “восстановить сигнал из его спектра”).

Идея метода фильтрации в спектральном пространстве (который также известен под названием “метод Фурье-фильтрации”) заключается в том, чтобы каким-то образом изменить спектр исходного сигнала и восстановить аудиосигнал из измененного спектра.

Таким образом, метод фильтрации реализуется в три шага:

1) производится вычисление спектра {Xn} исходного аудиосигнала {xn},

2) осуществляется изменение некоторого количества значений спектра {Xn} в соответствии желаемыми частотными свойствами фильтра, в результате чего получается измененный спектр {Yn},

3) выполняется формировании выходного аудиосигнала посредством вычисления обратного преобразования Фурье спектра {Yn}.

Процедура изменения спектра исходного сигнала при реализации методов линейной фильтрации реализуется как поэлементное умножение двух массивов: исходного спектра {Xn} и предварительно сформированного массива значений передаточной функции фильтра {Wn}:

Y W  X , для n  0,1, N 1.

При программной реализации метода фильтрации в спектральном пространстве, нужно обязательно выполнять требование комплексносопряженной симметрии для задаваемого массива {Wn}:

W_n  W*_N-n , n = 1,2….N/2-1,

где * означает операцию комплексного сопряжения (другими словами, если. например W2=0.5+j∙0.5, то нужно выполнить WN−2=0.5−j∙0.5). Значения W0 и WN/2 должны быть обязательно вещественными. Нужно заметить, что формула записана для случая, когда индексация массива начинается с нуля. В Matlab индексация элементов массивов начинается с единицы и формулу следует немного скорректировать достаточно очевидным образом.

3. Вариант задания

Вариант задания представлен на рисунке 1. Получается, что нужно реализовать фильтр высоких частот, ограниченных до 800 Гц.

Рисунок 1 – Вариант задания

4. Ход работы

Для работы используется песня, которую можно прослушать по ссылке: https://disk.yandex.ru/d/BS4dJNf00XmSpA [3]. Здесь чётко слышен мужской голос, в данном случае ставится цель как можно сильнее его подавить.

Для этого требуется cчитать данные с исходного сигнала, после этого определяется его спектр, который в дальнейшем модифицируется в соответствии с необходимыми требованиями. Из выходного спектра формируется новый аудиосигнал с помощью обратного преобразования Фурье. Также выводятся графики исходного и выходного сигнала, а также их амплитудные спектры. Код этой части работы представлен в листинге 1.

Листинг 1 – Код для фильтрации и визуализации сигналов

clc, clear, close all % очистка памяти

[input_signal,Fd] = audioread('любимая_песня_мии_уоллес.wav'); % звуковой файл

sound(input_signal,Fd); % проигрываем файл

N = length(input_signal); % Получить длину данных аудиофайла

t = 1:1:N;

plot(t./Fd,input_signal) % строим график сигнала

xlabel('Time'), ylabel('Audio Signal')

% вычисляем спектр сигнала по отдельности в каждом канале:

Spectr_input(:,1) = fft(input_signal(:,1));

Spectr_input(:,2) = fft(input_signal(:,2));

y = 20*log10(abs(Spectr_input(:,1))); % Преобразовать в дБ

f = [0:(Fd/N):Fd/2]; % Перевести абсциссу графика в Гц

% строим график амплитудного спектра входного сигнала

y = y(1:length(f));

figure(2),

semilogx(f,y); grid; axis([1 Fd/2 -100 100]) % изменяем пределы осей графика

xlabel('Частота (Гц)');

ylabel('Уровень (дБ)');

title('Амплитудный спектр исходного аудиосигнала');

legend('Audio');

% создаем пустой массив для последующей записи вых. сигнала:

output_signal_1 = zeros(N,2);

% создаем пустой массив для спектра вых. сигнала

% небольшая константа добавляется, чтобы избежать lg(0)

Spectr_output = zeros(size(Spectr_input)) + 0.00001;

% задаем граничные частоты полосы пропускания фильтра, в Герцах

lower_frequency = 800; % изменение нижней границы частоты

% переводим Герцы в целочисленные индексы массива: см. ф-лу (1)

n_lower_frequency = round(N * lower_frequency / Fd);

for n = 2:n_lower_frequency

Spectr_output(n,:) = Spectr_input(n,:);

Spectr_output(N+2-n,:) = Spectr_input(N+2-n,:);

end

% отдельно копируем элемент с наименьшим индексом:

Spectr_output(1,:) = Spectr_input(1,:);

% теперь вычитанием массивов создаем массив, в котором

% будут в наличии лишь компоненты

% с частотами от lower_frequency до upper_frequency

% т.е. будет реализован именно полосовой фильтр:

Spectr_output = Spectr_input - Spectr_output;

%посмотрим на график выходного спектра (только левый канал):

y=20*log10(abs(Spectr_output(:,1))); %Преобразовать в дБ

f=[0:(Fd/N):Fd/2]; %Перевести Абсциссу в Гц

y=y(1:length(f));

figure(3), semilogx(f,y); grid; axis([1 Fd/2 -100 100])

xlabel('Частота (Гц)'); ylabel('Уровень (дБ)');

title('Амплитудный спектр выходного сигнала аудиофайла');legend('Audio');

% обратное БПФ от модифицированного спектра:

% раздельно для каждого канала

output_signal_1(:,1) =ifft(Spectr_output(:,1));

output_signal_1(:,2) =ifft(Spectr_output(:,2));

% можно прослушать результат фильтрации прямо в Matlab:

sound(output_signal_1, Fd);

% выведем графики исходного аудиосигнала и после фильтрации:

% сейчас выводится весь график.

figure(4);

plot(input_signal);

% записываем новый аудиофайл:

audiowrite('любимая_песня_мии_уоллес_filtered.wav', output_signal_1, Fd)

Результаты обработки представлены на рисунках 2-5. Обработанный звук можно прослушать по ссылке: https://disk.yandex.ru/d/VLBmi6KhlkqH8A [4].

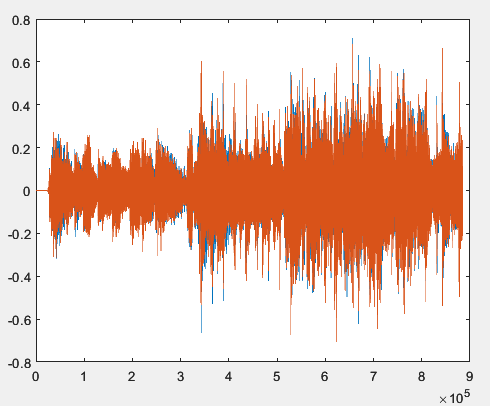
Рисунок 2 – График исходного сигнала

Рисунок 3 – Амплитудный спектр исходного сигнала

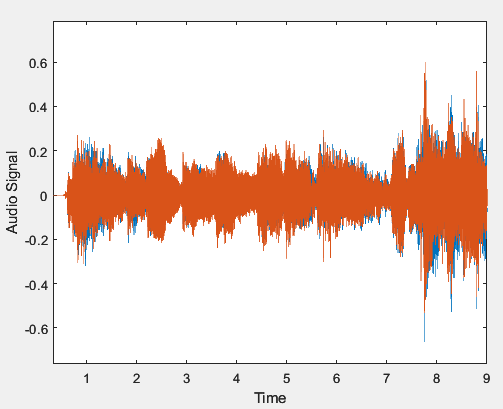
Рисунок 4 – График выходного сигнала (левый канал)

Рисунок 5 – Амплитудный спектр выходного сигнала

По рисунку 5 можно увидеть, что частоты ниже 800 Гц в выходном аудиосигнале глушатся, значит изменение амплитудного спектра работает корректно. По рисункам 2 и 4 заметно, что графики сигналов изменились, так как громкость звуков стала меньше.

Вывод

В ходе данной лабораторной работы я изучил методы формирования и изменения аудиосигналов с помощью средств MatLab.

Мной были разработаны программы для генерации и тестового сигнала и обработки аудио сигнала. Воспользовавшись полученными программами, получил изменённые сигналы и оценил изменения на слух и по графикам. Изменения были явно заметны: низкий мужской бас стал еле слышен, а музыка стала более приглушённой.

Список используемой литературы

1. Разработка программы для анализа звуковых файлов пакете MATLAB.// URL: https://gigabaza.ru/doc/106583.html

2. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №2 по дисциплине “Мультимедиа-технологии”, гр.4016,4017. ГУАП, 2024. – 10 с. // URL: https://pro.guap.ru/inside/student/tasks/3923806376828af8f0f7de44ae0bb3b8/download

3. Яндекс диск. Исходный звук. // URL: https://disk.yandex.ru/d/BS4dJNf00XmSpA

4. Яндекс диск. Обработанный звук. // URL: https://disk.yandex.ru/d/VLBmi6KhlkqH8A