ГУАП

КАФЕДРА 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, к.т.н. доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

Основы моделирования аудиосигналов средствами MATLAB

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

1. Цель.

Получить представление о принципах формирования аудиосигналов и приобрести навыки работы со звуковыми файлами с использованием MATLAB.

2. Краткие теоретические сведения о задачах обработки мультимедиа аудиоконтента.

Аудиоконтент является одной из составляющих мультимедиа. Оцифрованный звук сохраняют в файлах, данные в котором представлены в одном из стандартных форматов кодирования звука. Средства MATLAB позволяют считывать и записывать аудиоданные, закодированные в форматах *.wav и *.mp3, посредством стандартных команд:

[data,Fd] = audioread('имя файла на диске ПК'),

и

audiowrite('имя файла на диске ПК', data, Fd)

где data представляет собой массив аудиоданных (для записей, произведенных в режиме “моно”, массив будет одномерным, для стереозвука - двумерным), параметр Fd определяет частоту дискретизации. Для музыкальных файлов обычно используется стандартное значение частоты дискретизации 44100 Гц, хотя, при записи речевых сигналов нередко используется меньшее значение Fd=8000 Гц.

В результате выполнения функции audioread в переменную data будет перемещены все значения оцифрованного звука, хранящиеся в указанном файле. Строки матрицы data соответствуют отсчётам сигнала, столбцы – каналам, которых в звуковом файле может быть несколько.

В звуковом файле каждый отдельно взятый отсчёт оцифрованного сигнала представлен целым числом со знаком, лежащими в диапазоне либо от минус 128 до +127, либо от минус 32768 до +32767. Часто для улучшения точности обработки после считывания исходных данных из файла их дополнительно преобразуют в формат чисел с плавающей запятой (double), а перед записью в файл данных, полученных после обработки, необходимо производить преобразование из формата double в целочисленный формат.

3. Вариант задания

Вариант задания представлен на рисунке 1.

Рисунок 1 – Вариант задания

4. Ход работы

В первой части работы была написана программа, которая создаёт синусоидальный сигнал, громкость которого линейно увеличивается от нуля в начале записи до максимума в конце записи в левом канале и одновременно уменьшается от максимума до нуля в правом канале, при этом частота сигнала не изменяется на всем протяжении записи. Код программы представлен в листинге 1.

Листинг 1 – Формирование аудиосигнала

Fd = 44100; % задаем стандартную частоту дискретизации в Гц

Td = 1/Fd; % период дискретизации – обратный частоте

Ts = 6; % задаем длительность формируемого сигнала в секундах

N = Fd*Ts; %количество дискретных отсчетов

f_tone=440; % частота тона в Гц

y=zeros(N,2);

for n=1:N

nt = 2*pi*n*Td;

y(n,1) = sin(f_tone*nt) * n/N; % левый канал

y(n,2) = sin(f_tone*nt) * (1-n/N); % правый канал

end

output_signal = int16(32767*y); %задание разрядности данных

sound(y,Fd); %проигрываем смоделированный cигнал

% записываем новый аудиофайл:

audiowrite('audio_model.wav', output_signal, Fd);

Во второй части работы требуется cчитать данные с сформированного сигнала и построить визуализацию звуковой волны и амплитудного спектра. Код программы представлен в листинге 2.

Листинг 2 – Визуализация сигнала

clc, clear, close all %очистка памяти

[input_signal,Fd] = audioread('audio_model.wav');

N = length(input_signal);%Получить длину данных аудиофайла

t = 1:1:N;

% строим график сигнала целиком, для одного из каналов

plot(t./Fd,input_signal(:,1))

title('Звуковая волна аудиосигнала')

xlabel('Time'), ylabel('Audio Signal');

%вычисляем спектр сигнала в обоих каналах:

Spectr_input(:,1)=fft(input_signal(:,1)); % левый канал

Spectr_input(:,2)=fft(input_signal(:,2)); % правый канал

eps = 0.000001; % Малая константа, чтобы избежать lg(0)

y=20*log10(abs(Spectr_input(:,1))+eps); %Преобразовать в дБ

f=[0:(Fd/N):Fd/2]; %Перевести абсциссу графика в Гц

%строим график амплитудного спектра входного сигнала

% в одном из каналов (левом)

y=y(1:length(f));

figure(3),

semilogx(f,y); grid; axis([1 Fd/2 -100 100])

xlabel('Частота (Гц)');

ylabel('Уровень (дБ)');

title('Амплитудный спектр исходного аудиосигнала');

Результаты обработки представлены на рисунках 2-3.

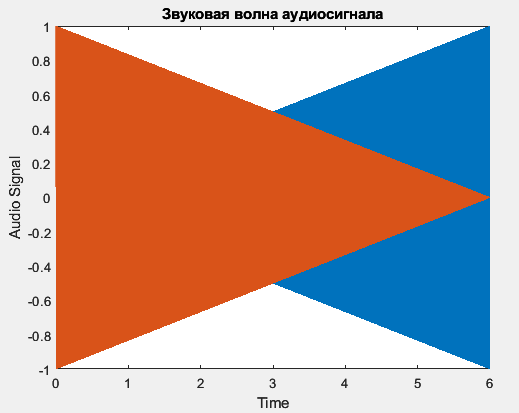
Рисунок 2 – Звуковая волна аудиосигнала

На рисунке 2 можно увидеть, что один из каналов линейно уменьшается от 1 до 0, а другой – наоборот. Значит сигнал согласно заданию сформирован верно.

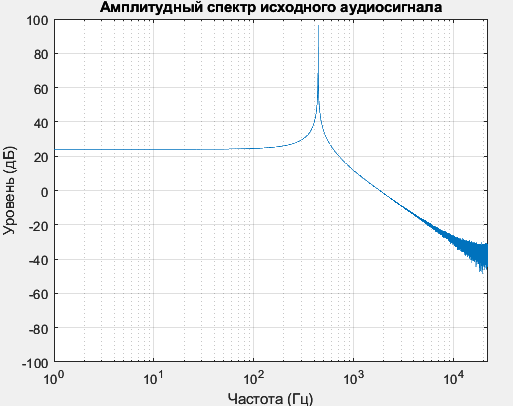
Рисунок 3 – Амплитудный спектр сигнала

Вывод

В данной лабораторной работе я научился считывать, создавать и сохранять звуковые сигналы, а также я познакомился с работой с данными аудиосигнала и визуализацией считываемых данных в среде Matlab.

Список используемой литературы

1. Разработка программы для анализа звуковых файлов пакете MATLAB.// URL: https://gigabaza.ru/doc/106583.html

2. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №1 по дисциплине “Мультимедиа-технологии “, испр. 21.02.2024. гр.4016,4017. ГУАП, 2024. – 7 с