lab2

ГУАП

КАФЕДРА 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

Стратегии распределения ресурсных блоков в централизованной сети со случайным трафиком

по курсу: МОДЕЛИРОВАНИЕ СИСТЕМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

Санкт-Петербург 2024

1.Цель.

Получение навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда». Изучение свойств алгоритмов планирования ресурсов нисходящего кадра в подобных системах. Изучение стратегий распределения ресурсных блоков в централизованной сети со случайным трафиком.

2.Краткие теоретические сведения

Известно, что для каждого абонента максимальная возможная скорость передачи данных или максимальная пропускная способность канала связи С

(Сhannel Сapacity) может быть выражена как:

данной формулы максимальная пропускная способность канала связи

при преодолении сигналов расстояния от БС к АБ и определяется следующим выражением:

2

В качестве модели затухания в помещениях (Indoor Propagation Model, IPM) в помещениях рассмотрим разработанной международным союзом связи (International Telecommunication Union, ITU). В рамках этой модели потери L в помещении рассчитывается следующим образом:

Далее необходимо вычислить приоритеты пользователей на основе разных алгоритмов. Во всех случаях, ресурсный блок будет отдан тому абоненту, у которого выше приоритет. Для показа примера вычислений

был рассмотрен пример расчетов для одного пользователя.

Первым был рассмотрен алгоритм Maximum Throughput, что

выделяет ресурсный блок тому пользователю, у которого максимальна пропускная канала связи. Приоритет пользователя i на ресурсный блок j

определяется как:

[ ] [ ]

Так, получаем приоритет для пользователя по алгоритму будет равен максимальной пропускной способности пользователя. Чтобы определить, кем будет занят блок нужно определить приоритет каждого из АБ, а после дать блок тому, у кого он больше. В случае этого алгоритма,

блок будет отдан тому, у кого больше пропускная способность в этом блоке.

Для других двух алгоритмов необходимо рассчитать среднюю скоростьна основе сглаженного фильтра по формуле:

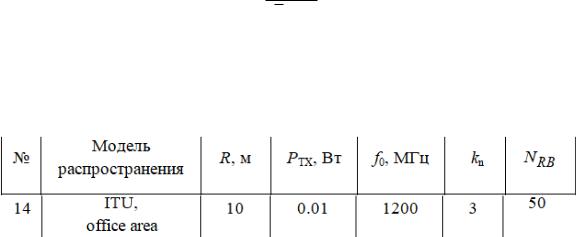
суммарного объёма данных, находящихся в буфере от параметра λ, что можно увидеть на рисунке 2.

Рисунок 2 – График зависимости среднего суммарного объёма данных в буфере от интенсивности входного потока для разных алгоритмов работы с буфером

Для каждого количества пользователей построен подробный график,

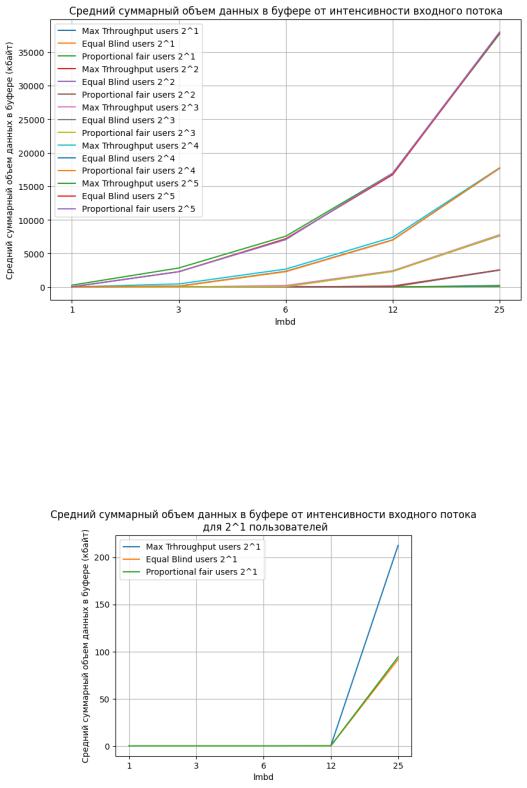
это представлено на рисунках 3-7.

Рисунок 3 – График зависимости среднего суммарного объёма данных в буфере от интенсивности входного потока для разных алгоритмов работы с буфером (2 пользователя)

5

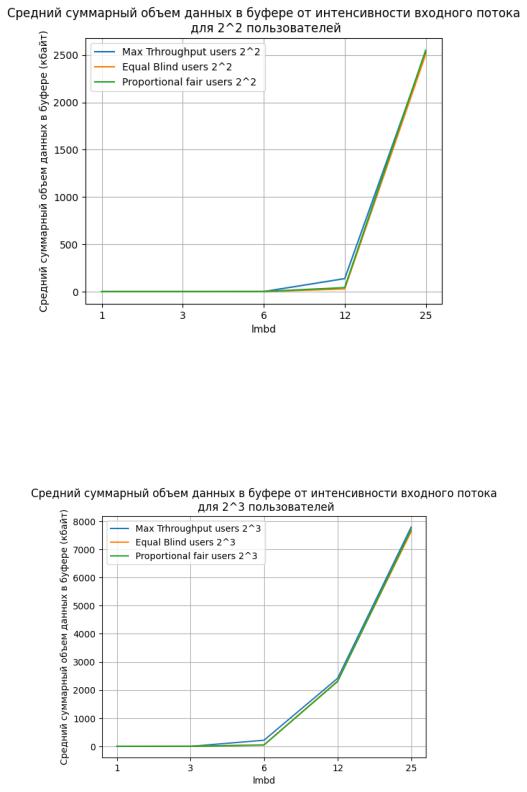
Рисунок 4 – График зависимости среднего суммарного объёма данных в буфере от интенсивности входного потока для разных алгоритмов работы с буфером (4 пользователя)

Рисунок 5 – График зависимости среднего суммарного объёма данных в буфере от интенсивности входного потока для разных алгоритмов работы с буфером (8 пользователя)

6

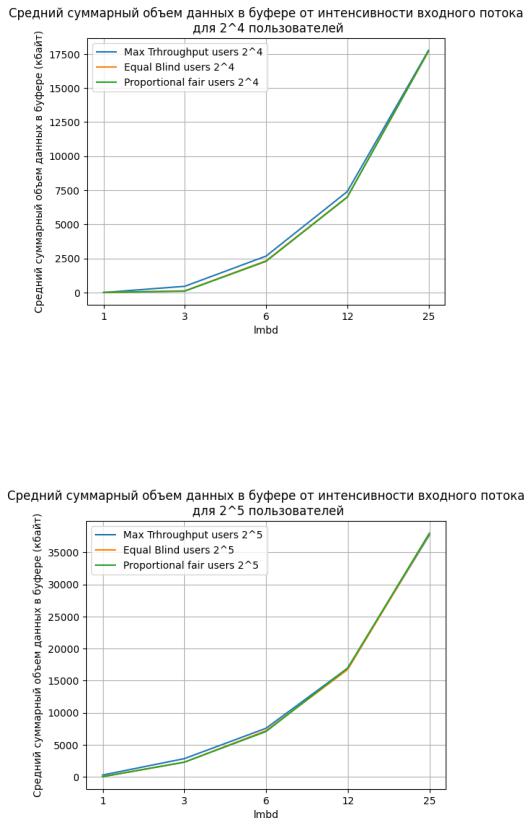
Рисунок 6 – График зависимости среднего суммарного объёма данных в буфере от интенсивности входного потока для разных алгоритмов работы с буфером (16 пользователя)

Рисунок 7 – График зависимости среднего суммарного объёма данных в буфере от интенсивности входного потока для разных алгоритмов работы с буфером (32 пользователя)

7

По графику видно, что все алгоритмы ведут себя схожим образом при одинаковом числе пользователей. При этом схожими остаются Equal Blind и Proportional fair, в то время как алгоритм Maximum Throughput показывает немного более худшие результаты – буфер больше заполнен в среднем при одинаковом значении интенсивности.

4.Вывод

В ходе выполнения работы были получены навыки моделирования стандартного сценария работы телекоммуникационных систем с топологией типа «звезда». Были изучены свойства алгоритмов планирования ресурсов нисходящего кадра, а также стратегии распределения ресурсных блоков в централизованной сети со случайным трафиком.

Исходя из результатов можно говорить, что самым оптимальными алгоритмами являются Equal Blind и Proportional fair, так как в среднем размер их буфера меньше, чем у Maximum Throughput хотя их значения приблизительно равны.

8

ПРИЛОЖЕНИЕ

import pandas as pd import numpy as np

import matplotlib.pyplot as plt

#from numba import njit, prange from tqdm import tqdm

#Определение параметров по варианту

K_boltsman = 1.38 * ( 10**(-23) ) # Постоянная Больцмана

t_rb = 0.0005 # Длина слота, с

y = 1 # Длина временного промежутка, с y_full = 10 # Весь временной промежуток, с delta_f = 180 # delta f кГц

T = 300 # Темература

K_const = 29 # Константа из формулы

def get_L(f0, Rmax):

# Создаем случайный радиус до вышки

r = np.sqrt(np.random.uniform(0, Rmax**2))

# Считаем потери

L = 10**((20 * np.log10(f0) + K_const * np.log10(r) - 28) / 10) return L

cur_L = 10**((20 * np.log10(f0) + K_const * np.log10(15) - 28) / 10)

# Мощность шума

P_n = delta_f * T * K_boltsman * k_n

# Мощность принятая абонентом

P_rx = p / (cur_L) # Затухание со случайной величиной

# Соотношение сигнал/шум

SNR = P_rx / P_n

# Пропускная способность канала связи np.log2(1+SNR)

# Функция расчета максимальной пропускной способности

9

def get_C(cur_L):

# Мощность шума

P_n = delta_f * T * K_boltsman * k_n

# Мощность принятая абонентом

P_rx = p / (cur_L) # Затухание со случайной величиной

# Соотношение сигнал/шум

SNR = P_rx / P_n

# Пропускная способность канала связи cur_C = delta_f * np.log2(1+SNR) return cur_C*125 # из Мбит в Кбайт

# Получение массивов L, C, V для одного пользователя def get_user_frame(user_L, n_slots, lmbd):

L_list = []

C_list = []

# Для каждого слота

for k in range(n_slots):

L_list.append([None for i in range(N_rb)])

C_list.append([None for i in range(N_rb)])

# Для каждого ресурсного блока for j in range(N_rb):

# Генерируем шум со случайной нормальной величиной

L_list[k][j] = user_L + np.random.normal(0,1)

# Считаем максимальную пропускную способность в зависимости от

шума

C_list[k][j] = get_C(L_list[k][j])

# Массив с объемом данных, который приходит в каждом слоте

V_list = []

# Для каждого слота генерируем объем данных в кбайт for k in range(n_slots):

V_list.append(np.random.poisson(lmbd))

return V_list, L_list, C_list

# Алгоритм Maximum Throughput

def maximum_throughput(C_list, V_list):

# Массив с распределением ресурсных блков по пользователям choice_list = []

# Для каждого слота

for k in range(len(C_list[0])):

choice_list.append([None for j in range(len(C_list[0][0]))]) v_sums = [V_list[u][k] for u in range(len(V_list))]

10