lab1

ГУАП

КАФЕДРА 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ст. преподаватель				Н.В. Апанасенко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

Механизмы распределения ресурсов нисходящего кадра в телекоммуникационных сетях

по курсу: МОДЕЛИРОВАНИЕ СИСТЕМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

1. Цель.

Получение навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда». Изучение свойств алгоритмов планирования ресурсов нисходящего кадра в подобных системах.

2. Краткие теоретические сведения

Известно, что для каждого абонента максимальная возможная скорость передачи данных или максимальная пропускная способность канала связи С (Сhannel Сapacity) может быть выражена как:

где - полоса пропускания канала связи, - отношение сигнал/шум (Signal-to-Noise Ratio, SNR) у абонента с индексом . Как видно из данной формулы максимальная пропускная способность канала связи зависит от двух параметров, и если значение фиксировано, то значение параметра в общем случае является случайной величиной, зависящей от многих факторов.

где - принятая мощность сигнала, - мощность теплового шума. Мощность теплового шума определяется следующим выражением:

здесь T – абсолютная температура (К), k – постоянная Больцмана , - коэффициент теплового шума приемника .

Очевидным является тот факт, что принятая мощность сигнала определяется излучаемой мощностью БС - и уровнем потерь мощности при преодолении сигналов расстояния от БС к АБ и определяется следующим выражением:

В качестве модели затухания в помещениях (Indoor Propagation Model, IPM) в помещениях рассмотрим разработанной международным союзом связи (International Telecommunication Union, ITU). В рамках этой модели потери L в помещении рассчитывается следующим образом: где K – коэффициент, зависящий от типа помещения, – принять равным нулю, К – принять равным 29. Далее рассмотрим алгоритмы распределения ресурсов, реализованные на базовой станции. Введем коэффициент , показывающий какая доля ресурсов (например, времени) выделяется i-му абоненту. , С учетом введенного коэффициента результирующая скорость для АБ с индексом i принимает следующий вид Тогда суммарная скорость передачи БС определяется следующим выражением: Соответственно средняя суммарная скорость среди абонентов может быть рассчитана как:

3. Ход работы

Пример случайного расположения абонентов представлено на рисунке 1. Этот рисунок содержит в себе список значений расстояния от АБ до БС в пределах заданного радиуса согласно варианту.

Рисунок 1 – Расположение абонементов

Далее согласно формулам генерируются максимально достижимые скорости для сформированных абонентов. В программе производится расчет коэффициентов деления ресурсов канала между абонентами для трех типов планировщиков: планировщика, обеспечивающего равные скорости абонентам (ПРС), планировщика, обеспечивающего максимальную суммарную скорость передачи данных (ПСС) и планировщика, обеспечивающего равные доли выделенных ресурсов (ПРД).

Для всех трех алгоритмов планирования рассчитываются величины суммарной скорости передачи , средней скорости , а также средней минимальной скорости среди всех абонентов .

Повторяя случайное размещение абонентов необходимое число раз (min 100), строятся графики зависимости оценок , и от числа абонентов в сети N. Количество абонентов равны N = 1, 2, 4, 8,…, 64. Эти графики представлены на рисунках 2-4.

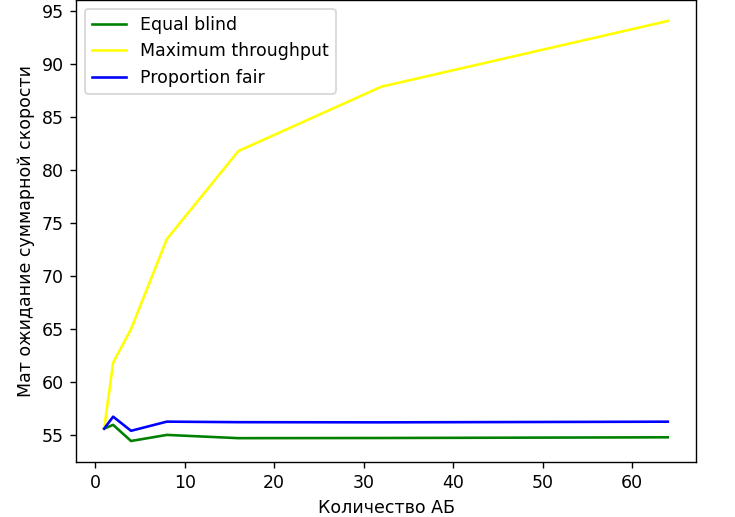
Рисунок 2 – График суммарной скорости передачи в зависимости от кол-ва АБ

На рисунке 2 можно увидеть, что с увеличением количества абонентов суммарная скорость алгоритма Maximum Throughput существенно увеличивается. Остальные два алгоритма имеют примерно один и тот же уровень.

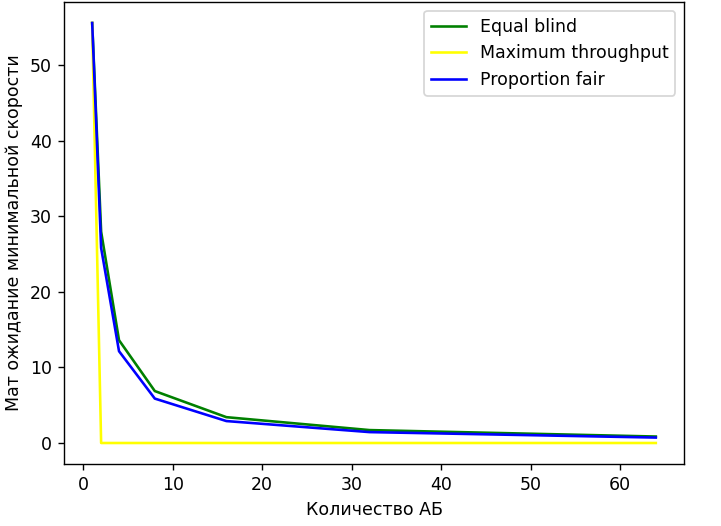
Рисунок 3 - График минимальной скорости передачи в зависимости от кол-ва АБ

На рисунке 3 видно, что с увеличением количества АБ, также минимальная скорость передачи данных снижается. Исключение составляет только алгоритм Maximum Throughput, так как одному единственному абоненту достаётся вся доля ресурсов.

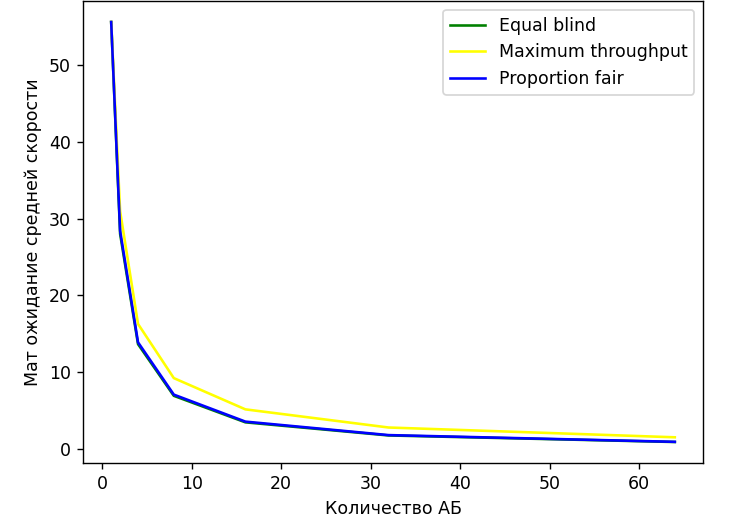
Рисунок 4 - График средней скорости передачи в зависимости от кол-ва АБ

На рисунке 4 видно, что с увеличением количества абонентов, средняя скорость в каждом алгоритме почти одинаковая, но Maximum Throughput справляется чуть лучше.

4. Вывод

В ходе данной лабораторной работы получены навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда», а также изучены свойства алгоритмов планирования ресурсов нисходящего кадра в подобных системах.

Также были сравнены средние, минимальные и сумма скоростей при разных типах планирования деления ресурсов между АБ. Лучше всего справился алгоритм Maximum Throughput, так как его показатели суммарной и средних скоростей выше, хотя при этом есть недостаток, где чем дальше АБ находится от БС, тем дольше он будет ждать момента обслуживания его заявки. Алгоритм Equal Blind и Proportion Fair справились почти одинаково.

Очевидно, что с увеличением количества абонентов в сети минимальная и средняя скорости передачи данных уменьшается.

В ходе лабораторной работы проблем не возникло.

ПРИЛОЖЕНИЕ

import random

import math

import numpy as np

import matplotlib.pyplot as plt

DELTA_F = 5 * 10**6

R = 50 # Макс радиус

PTX = 0.1

F0 = 5600

KN = 2

KB = 1.38 * 10**(-23) # Постоянная Больцмана

T = 300 # Абсолютная температура

def generation_distances(N):

'''Генерация расстояний от АБ до БС'''

d = []

for i in range(N):

d.append(np.sqrt(random.uniform(1, R**2)))

return d

def finding_channel_capicity(distances):

'''Рассчёт макс пропускной способности'''

Pn = DELTA_F * T * KB * KN # Мощность теплового шума

C = [] # пропускная способность

for i in range(len(distances)):

loose = (20 * np.log10(F0) + 29 * np.log10(

distances[i]) - 28)

L = (10**(loose/10)) # Потеря мощности

Prx = PTX/L # Приянтая мощность сигнала

SNR = Prx/Pn # Сигнал/шум

C.append(DELTA_F*math.log2(1+SNR) * 10**(-6))

return C

def equal_blind(capicity):

'''Равные скорости между абонентами'''

promez = 0

for i in range(len(capicity)):

promez += 1/capicity[i]

D = []

for _ in range(len(capicity)):

D.append(1/promez)

return sum(D), min(D), np.mean(D)

def maximum_throughput(capicity):

'''Макс скорость для ближ абонента'''

D = []

max_C = max(capicity)

for i in range(len(capicity)):

if capicity[i] == max_C:

D.append(max_C)

else:

D.append(0)

return sum(D), min(D), np.mean(D)

def proportion_fair(capicity):

'''Равные доли скорости'''

D = []

N = len(capicity)

for i in range(N):

D.append(capicity[i]/N)

return (sum(capicity)/N), min(D), np.mean(D)

def main():

N = [2**i for i in range(7)] # Количество пользователей

# Итоговые значения equal blind

D_sum_1_final, D_min_1_final, D_mean_1_final = [], [], []

# Итоговые значения maximum throughput

D_sum_2_final, D_min_2_final, D_mean_2_final = [], [], []

# Итоговые значения proportion_fair

D_sum_3_final, D_min_3_final, D_mean_3_final = [], [], []

for i in range(len(N)):

# Промежуточные значения equal_blind

D_sum_1, D_min_1, D_mean_1 = [], [], []

# Промежуточные значения maximum throughput

D_sum_2, D_min_2, D_mean_2 = [], [], []

# Промежуточные значения proportion_fair

D_sum_3, D_min_3, D_mean_3 = [], [], []

for _ in range(101):

d = generation_distances(N[i])

C = finding_channel_capicity(d)

summa, minimal, srednee = equal_blind(C)

D_sum_1.append(summa)

D_min_1.append(minimal)

D_mean_1.append(srednee)

summa, minimal, srednee = maximum_throughput(C)

D_sum_2.append(summa)

D_min_2.append(minimal)

D_mean_2.append(srednee)

summa, minimal, srednee = proportion_fair(C)

D_sum_3.append(summa)

D_min_3.append(minimal)

D_mean_3.append(srednee)

D_sum_1_final.append(np.mean(D_sum_1))

D_min_1_final.append(np.mean(D_min_1))

D_mean_1_final.append(np.mean(D_mean_1))

D_sum_2_final.append(np.mean(D_sum_2))

D_min_2_final.append(np.mean(D_min_2))

D_mean_2_final.append(np.mean(D_mean_2))

D_sum_3_final.append(np.mean(D_sum_3))

D_min_3_final.append(np.mean(D_min_3))

D_mean_3_final.append(np.mean(D_mean_3))

# График сумм

plt.plot(N, D_sum_1_final, color='green', label='Equal blind')

plt.plot(N, D_sum_2_final, 'yellow', label='Maximum throughput')

plt.plot(N, D_sum_3_final, 'blue', label='Proportion fair')

plt.legend()

plt.title('Сравнение графиков суммарной скорости передачи в зависимости от кол-ва АБ')

plt.xlabel('Количество АБ')

plt.ylabel('Мат ожидание суммарной скорости')

plt.show()

# График мин скорости

plt.plot(N, D_min_1_final, color='green', label='Equal blind')

plt.plot(N, D_min_2_final, 'yellow', label='Maximum throughput')

plt.plot(N, D_min_3_final, 'blue', label='Proportion fair')

plt.legend()

plt.title('Сравнение графиков минимальной скорости передачи в зависимости от кол-ва АБ')

plt.xlabel('Количество АБ')

plt.ylabel('Мат ожидание минимальной скорости')

plt.show()

# График средней скорости

plt.plot(N, D_mean_1_final, color='green', label='Equal blind')

plt.plot(N, D_mean_2_final, 'yellow', label='Maximum throughput')

plt.plot(N, D_mean_3_final, 'blue', label='Proportion fair')

plt.legend()

plt.title('Сравнение графиков средней скорости передачи в зависимости от кол-ва АБ')

plt.xlabel('Количество АБ')

plt.ylabel('Мат ожидание средней скорости')

plt.show()

main()