ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ст. преподаватель				Б.К. Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №7

Позиционные игры

по курсу: ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2023

1. Цель работы

Освоить и закрепить практические навыки по принятию и обоснованию решений в условиях недостатка информации, когда один из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы».

2. Ход работы

Вариант 16 представлен на рисунке 1.

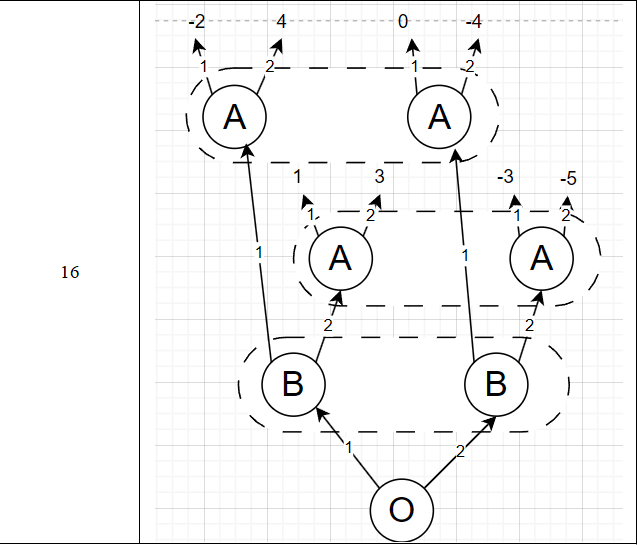
Рисунок 1 – Вариант задания

Так как игрок B не знает первый случайный ход, то он имеет лишь две стратегии: B₁ – выбрать y=1 и B₂ – выбрать y=2.

Так как игрок А не знает случайный и знает ход B, то он имеет тогда такие стратегии: А₁ – [1, 1], А₂ – [1, 2], А₃ – [2, 1], А₄ – [2, 2].

Таблицу выигрышей игрока, а также матрицу игры необходимо составить для каждого из вариантов случайного выбора.

При x=1:

		B1	B2
		y=1	y=2
A1	[1, 1]	W(1, 1, 1)	W(1, 2, 1)
A2	[1, 2]	W(1, 1, 1)	W(1, 2, 2)
A3	[2, 1]	W(1, 1, 2)	W(1, 2, 1)
A4	[2, 2]	W(1, 1, 2)	W(1, 2, 2)

При x=2:

		B1	B2
		y=1	y=2
A1	[1, 1]	W(2, 1, 1)	W(2, 2, 1)
A2	[1, 2]	W(2, 1, 1)	W(2, 2, 2)
A3	[2, 1]	W(2, 1, 2)	W(2, 2, 1)
A4	[2, 2]	W(2, 1, 2)	W(2, 2, 2)

Искомая матрица игры рассчитывается исходя из вероятности выбора каждого случайного значения x. Так, в искомой матрице первый элемент будет равен 0.5*(-2)+0.5*0=-1. Остальные элементы рассчитывается таким же образом.

После применения отношений доминирования (остаётся строка A₃ и столбец B₁):

[0]

Тогда цена игры равна 0 в любом случае, игроку А невыгодно играть в любом случае, так как он не получает никакого выигрыша в лучшем случае при выборе 3-й или 4-й стратегии. Игрок B будет выбирать только первую стратегию.

3. Вывод

В ходе лабораторной работы я освоил процесс нормализации позиционной игры. В частности, была решена задача с неполной информацией.

В ходе работы проблем не возникло.