lab4

1.Цель работы

Изучение метода поиска экстремума нелинейной функции нескольких переменных.

2.Ход работы

Вариант 6 представлен на рисунке 1. Здесь представлена исследуемая функция.

Рисунок 1 – Вариант задания

Находятся экстремумы функции ручным подсчѐтом, это представлено на рисунке 2.

Рисунок 2 – Ручной поиск экстремума

Вданной функции есть только одна точка экстремума, где x1=4, x2=-5.

ВMathcad вводится данная функция, находятся еѐ производные первого порядка, это представлено на рисунке 3.

2

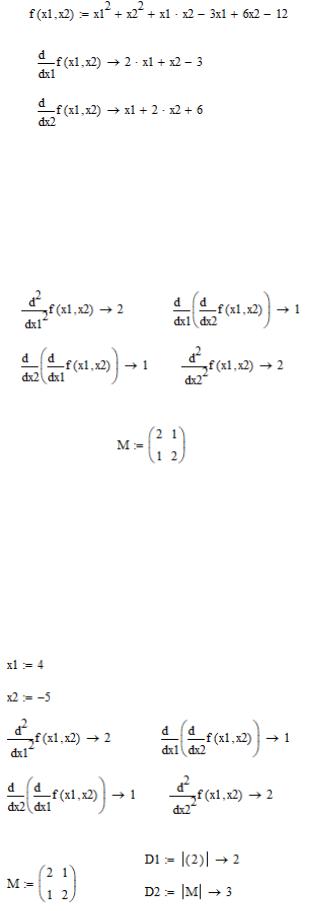
Рисунок 3 – Поиск производных первого порядка в MathCad

Теперь находятся производные второго порядка, на основе чего строится матрица Гессе. Это представлено на рисунке 4.

Рисунок 4 – Поиск производных второго порядка в MathCad

Так как все ячейки матрицы Гессе являются константами, то матрица не требует перерасчѐта. Тогда итоговый для неѐ ответ представлен на рисунке 5, здесь же рассчитываются миноры функции.

Рисунок 5 – Расчѐт миноров функции

3

Так как угловые миноры строго положительны, то данная матрица является положительно определѐнной согласно критерию Сильвестра.

Также выясняется, является ли найденный экстремум минимумом или максимумом:

минимумом.

3.Вывод

Врезультате выполнения лабораторной работы были изучены методы поиска экстремума нелинейной функции нескольких переменных. Была построена матрица Гессе и найдены все угловые и главные миноры, которое показали, что матрица является положительно определѐнной. В результате был найден один единственно существующий экстремум-минимум.

Входе работы проблем не возникло.

4