ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ст. преподаватель				Б.К. Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

Решение одномерное задачи оптимизации

по курсу: ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2023

1. Цель работы

Изучение алгоритмов поиска экстремума унимодальной функции, определение сравнительной эффективности методов одномерной оптимизации.

2. Ход работы

Вариант 6 представлен на рисунке 1. В первой ячейке указана функция, во второй – интервал исследования, в третьей – погрешность определения экстремума.

Рисунок 1 – Вариант задания

Для начала аналитически рассчитываем точку экстремума:

y = sin(x + )

y’ = cos(x + )

cos (x + ) = 0 => x = + π * k

Рассмотрим график функции на промежутке [π; 2π], который представлен на рисунке 2. На этом промежутке экстремум (т.е. минимум) достигается при x = (~4,188), что соответствует построенному графику.

Рисунок 2 – График функции y = sin(x + )

Для поиска экстремума унимодальной функции используем следующие алгоритмы:

1. Метод равномерного поиска, где задается начальный интервал неопределенности и количество вычислений, вычисления производятся в равноотстоящих друг от друга точках, при этом интервал делится на равных интервалов, путем сравнения величин находится точка, в которой значение функции наименьшее;

2. Метод дихотомии, который позволяет исключать в точности половину интервала на каждой итерации, после вычисления значения функции в середине интервала одна часть интервала отбрасывается так, чтобы функция имела разный знак на концах оставшейся части, итерации метода деления пополам прекращаются, если интервал становится достаточно малым;

3. Метод золотого сечения - метод поиска экстремума действительной функции одной переменной на заданном отрезке, в основе метода лежит принцип деления отрезка в пропорциях золотого сечения;

4. Метод Фибоначчи - это улучшение реализации поиска с помощью золотого сечения, служащего для нахождения минимума/максимума функции. Подобно методу золотого сечения, он требует двух вычислений функции на первой итерации, а на каждой последующей только по одному. Однако этот метод отличается от метода золотого сечения тем, что коэффициент сокращения интервала неопределенности меняется от итерации к итерации.

Результат выполнения кода, представленного в Приложении, для поиска экстремума заданной функции представлен на рисунке 3.

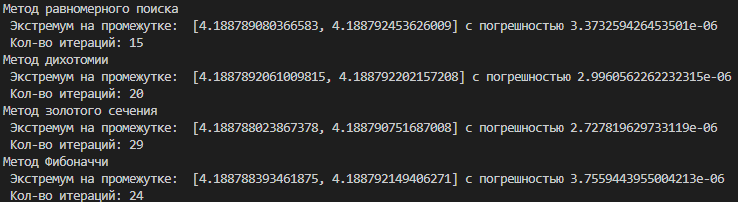
Рисунок 3 – Результаты работы программы

Для более наглядной оценки качества работы методов был построен график зависимости числа итераций от погрешности для всех методов, который представлен на рисунке 4.

Рисунок 4 – График зависимости числа итераций от погрешности

3. Вывод

В ходе лабораторной работы были изучены различные методы поиска экстремума для заданной функции. В результате самым лучшим методом оказался именно метод равномерного поиска, который выполнил задачу за 15 итераций. Неплохой результат, но это не умаляет эффективность метода дихотомии, которому потребовалось всего на 5 итераций больше для поиска. Это ожидаемо, так как фактически эти методы одинаковы, только в равномерном поиске количество интервалов на каждой итерации задано изначально и оно больше двух. Что касается методов золотого сечения и метода Фибоначчи, то они справились, к сожалению, хуже всего. Им уже потребовалось значительно больше итераций, что делает их использование при работе неэффективным.

В ходе работы проблем не возникло.

Приложение

import numpy as np

from matplotlib import pyplot as plt

eps = 2**(-18)

a = np.pi

b = np.pi*2

def f(x):

return np.sin(np.pi/6+x)

def f_list(x):

result = []

for i in x:

result.append(f(i))

return result

def uniform_search(start, end, number_of_intervals):

N = 0

result = []

while (abs(end-start) > eps):

x = np.arange(start, end, (end-start)/number_of_intervals)

values = f_list(x)

# Ищем интервал, где f(x) min

min_index = values.index(min(values))

start, end = x[min_index-1], x[min_index+1]

N += 1

result.append(end-start)

return (start, end, result, N)

def dichotomy_search(start, end):

N = 0

result = []

while (abs(end-start) > eps):

n = (start+end)/2

x = [(start+n)/2, (end+n)/ 2]

values = f_list(x)

(end, start) = (n, start) if values[0] < values[1] else (end, n)

N += 1

result.append(end-start)

return (start, end, result, N)

def golden_ratio(start, end):

N = 0

result = []

while (abs(end-start) > eps):

x = [end-(end-start)*0.618, start+(end-start)*0.618]

values = f_list(x)

if values[0] < values[1]:

end = x[1]

else:

start = x[0]

N += 1

result.append(end-start)

return (start, end, result, N)

def fibonachi(start, end):

N = 1

result = []

fib = [1, 1]

while ((end - start) / fib[-1] > eps):

fib.append(fib[-2] + fib[-1])

while (abs(end-start) > eps):

x = [start + (end - start) * (fib[len(fib) - 1 - N] / fib[len(fib) - N]),

start + (end - start) * (fib[len(fib) - 1 - N] / fib[len(fib) - N])]

# Если x одинаковы, то добавить небольшую разницу

if x[0] == x[1]:

x[1] += (end - start)/10

values = f_list(x)

if values[1] < values[0]:

start = x[0]

else:

end = x[1]

N += 1

result.append(end-start)

return (start, end, result, N-1)

def main():

start, end, result, N = uniform_search(a, b, 5)

print('Метод равномерного поиска\n Экстремум на промежутке: ',

[start, end], 'c погрешностью', result[-1], '\n Кол-во итераций:', N)

plt.plot(result, range(N), label = 'Метод равномерного поиска')

start, end, result, N = dichotomy_search(a, b)

print('Метод дихотомии\n Экстремум на промежутке: ',

[start, end], 'c погрешностью', result[-1], '\n Кол-во итераций:', N)

plt.plot(result, range(N), label = 'Метод дихотомии')

start, end, result, N = golden_ratio(a, b)

print('Метод золотого сечения\n Экстремум на промежутке: ',

[start, end], 'c погрешностью', result[-1], '\n Кол-во итераций:', N)

plt.plot(result, range(N), label = 'Метод золотого сечения')

start, end, result, N = fibonachi(a, b)

print('Метод Фибоначчи\n Экстремум на промежутке: ',

[start, end], 'c погрешностью', result[-1], '\n Кол-во итераций:', N)

plt.plot(result, range(N), label = 'Метод Фибоначчи')

plt.legend()

plt.show()

if __name__ == "__main__":

main()