lab5

1)Цель работы

Нахождение экспериментальной зависимостей Q(λ, µ0, N0) и T(λ, µ0, N0)

для элементарной системы массового обслуживания с буфером объема N.

Вариант 16

Во втором столбце записан закон распределения входного потока заявок, в третьем – закон распределения времени обслуживания заявок, в

четвёртом - µ0, в пятом - объем буфера N.

2)Ход работы

Записывается формула и строится график экспоненциальный,

используемый для распределения заявок на входе. Это представлено на рисунке 1.

Формула: f(x;λ)= λ*e-λx

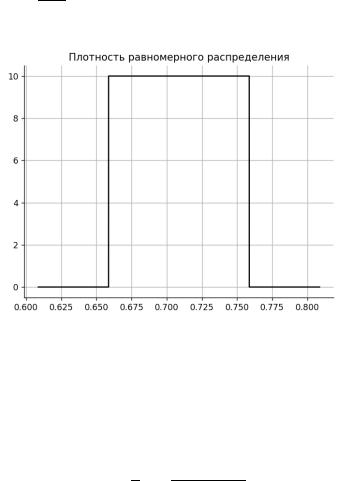
Рисунок 1 – Плотность экспоненциального распределения Записывается формула и строится график равномерного

распределения, используемый для распределения времени обслуживания заявок на выходе. Это представлено на рисунке 2.

2

Формула: f(x) ={

Рисунок 2 – Плотность равномерного распределения Проводится моделирование работы СМО с буфером. Одним из

критериев для вычисления является поиск среднего времени пребывания запроса в системе, которое вычисляется по формуле:

T = * ∑ ( )

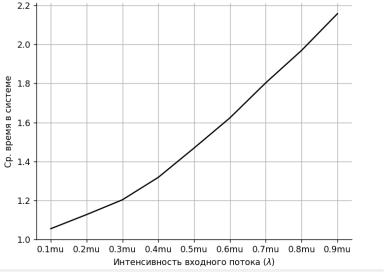
Моделируется работы системы такой системы. Записывается зависимость среднего времени пребывания запроса от интенсивности входного потока. Это представлено на рисунке 3.

.

Рисунок 3 – Моделирование для экспериментальной зависимости

среднего времени задержки

3

При проведении моделирования работы СМО также вычисляется критерий подсчёта производительности такой системы, которая вычисляется по формуле:

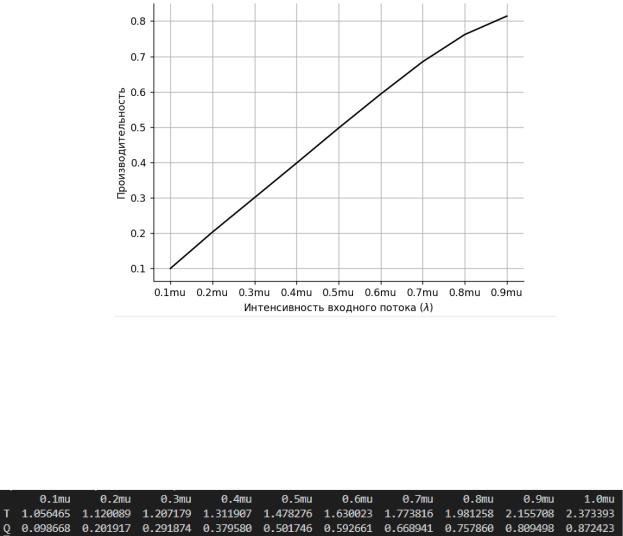
Записывается зависимость производительности от интенсивности входного потока. Это представлено на рисунке 4.

Рисунок 4 – Моделирование для экспериментальной зависимости производительности

Таблица с подробными экспериментальными данными о среднем времени пребывания в системе и средней производительности системы представлена на рисунке 5.

Рисунок 5 - Данные о зависимости среднего времени пребывания запроса от интенсивности входного потока

В программе выполняются моделирования теоретическое и экспериментальное (при заданных по варианту данных) для обоих критериев.

График сравнения зависимостей моделирований для среднего времени задержки представлен на рисунке 6. График сравнения зависимостей

4

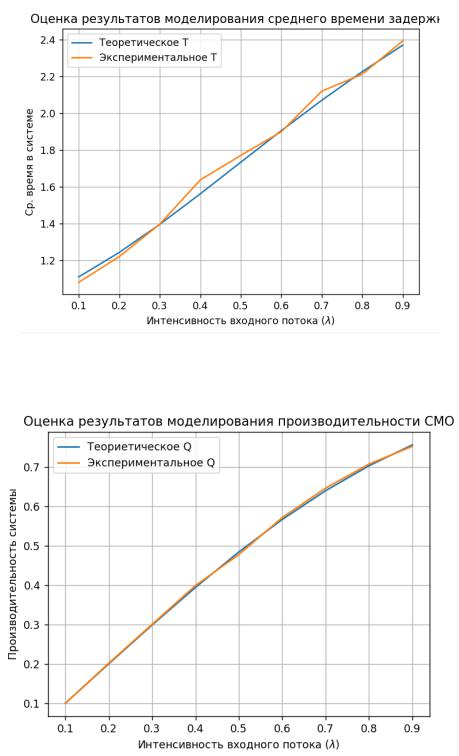
моделирований для производительности представлен на рисунке 7. При этом погрешность расхождений не превышает 1%. Код выполнения программы представлен в Приложении.

Рисунок 6 – Оценка результатов моделирования среднего времени задержки

Рисунок 7 – Оценка результатов моделирования производительности

5

3)Вывод

В ходе данной лабораторной работы я познакомился с элементарной системой массового обслуживания с конечным буфером. В ходе моделирования теоретической и экспериментальной было выяснено, что при увеличении интенсивности входного потока среднее время пребывания в системе сильно увеличивается. При этом, сравнивая среднее время задержки между системами с бесконечным и конечным буфером, сразу заметно, что моделирование такой системы проходит заметно быстрее. Это связано с тем,

что при заполнении буфера СМО отбрасывает поступающую заявку, и она просто не будет выполняться. Производительность также возрастает при увеличении интенсивности входного потока. Это значит не только, что нагрузка на систему небольшая, и она вполне справляется с такой работой,

но и то, что конечный буфер позволяет системе работать вполне быстро, где заявки не будут долго ждать своей очереди для выполнения.

В ходе работы проблем не возникло.

6

Приложение

import sys

import numpy as np import pandas as pd

import matplotlib.pyplot as plt

from scipy.stats import uniform, expon

def __plot__(figure, arr_x, arr_y=None, title='', xlabel='', ylabel='', legend: str = None, color=''):

fig = plt.figure(figure)

ax = fig.add_axes((0.1, 0.1, 0.8, 0.8)) ax.spines['right'].set_color('none') ax.spines['top'].set_color('none')

if arr_y is None:

ax.plot(arr_x, label=legend, color=color) else:

ax.plot(arr_x, arr_y, label=legend, color=color) ax.grid()

ax.set_title(title) ax.set_ylabel(ylabel) ax.set_xlabel(xlabel) if legend is not None:

ax.legend()

def plot_expon_distribution(lambda_, figure):

# Определение границ графика:

temp = expon.rvs(scale= 1/lambda_, size=10000) x_min, x_max = min(temp), max(temp)

# Построение графика:

x = np.linspace(x_min, x_max, 1000) y = expon.pdf(x, scale=1/lambda_)

title = 'Плотность экспоненциального распределения распределения'

__plot__(figure, x, y, title, color='black')

def plot_uniform_distribution(a, b, figure):

# Определение границ интервала

7

x_min, x_max = a - 0.05, b + 0.05

# Построение графика

x = np.linspace(x_min, x_max, 10000) y = uniform.pdf(x, loc=a, scale=b-a)

title = 'Плотность равномерного распределения'

__plot__(figure, x, y, title=title, color='black')

def model_of_queuing_system(mu, l, is_test, N): a = 1 / mu - 0.05 * mu

b = a + 0.1 * mu

new_t_income = lambda: expon.rvs(scale=1 / l)

new_t_outcome = lambda: expon.rvs(scale= 1 / mu) if is_test else uniform.rvs(loc=a, scale=b-a)

# системное время ts = 0

# занятость ОУ busy = False

# момент поступления заявки t_in = new_t_income() t_ins = []

# момент освобождения ОУ t_out = t_in

t_outs = []

n, k, m = 0, 0, 0

t_mean_old = sys.float_info.max counter = 0

# производительность q_mean_old = 2**32 q_data = []

while True: counter += 1

# Проверяем наступило ли время освобождения ОУ if t_in <= t_out:

# Записываем в системное время момент поступления заявки ts = t_in

n += 1 # Увеличиваем счетчик поступивших заявок

#Сохраняем в список момент поступления заявки

#t_ins.append(t_in)

8

if not busy or m < N: t_ins.append(t_in)

# Генерируем момент поступления заявки t_new = new_t_income() q_data.append(t_new)

# Система обрабатывает сейчас заявку? if not busy:

busy = True

t_out = ts + new_t_outcome() elif m < N:

m += 1

# Вычисляем следующий момент поступления заявки t_in = ts + t_new

else:

# Записываем в системное время момент освобождения ОУ ts = t_out

k += 1 # Увеличиваем счетчик обслуженных заявок

# Сохраняем в список момент освобождения ОУ t_outs.append(t_out)

# В буфере больше 0 заявок? if m > 0:

m -= 1

t_out = ts + new_t_outcome() else:

busy = False t_out = t_in

# Ошибка удовлетворительная? if counter % 1000 == 0:

t_mean_new = np.mean([t_outs[i] - t_ins[i] for i in range(len(t_outs))])

q_mean_new = (k/n) / np.mean(q_data)

if (abs((t_mean_new - t_mean_old) / t_mean_old) < 0.001): return t_mean_new, q_mean_new

t_mean_old = t_mean_new q_mean_old = q_mean_new

def experiment(mu, is_test, figure, N):

# Параметры для тестирования

lambdas = np.linspace(0.1, 1, 10) * mu T_theoretical = []

T_experimental = []

9

Q_theoretical = []

Q_experimental = []

# Сбор практических данных for l in lambdas:

t, q = model_of_queuing_system(mu, l, is_test, N) T_experimental.append(t) Q_experimental.append(q)

if is_test:

# Сбор теоретических данных for l in lambdas:

# Подсчёт среднего времени ro = l / mu

T_theoretical.append(1/l*sum( (i * (1-ro) * ro**i) / (1 - ro**(N+1)) for i in range(N+2) ))

# Подсчёт производительности

Potkl = ((1 - ro)*(ro**N))/(1-ro**(N+1))

Q_theoretical.append(l*(1-Potkl))

# Построение теоретического графика времени plt.figure(figure)

plt.plot(lambdas[:9], T_theoretical[:9], label="Теоретическое T") plt.plot(lambdas[:9], T_experimental[:9], label="Экспериментальное

T")

plt.legend()

plt.title("Оценка результатов моделирования среднего времени задержки")

plt.ylabel("Ср. время в системе") plt.xlabel("Интенсивность входного потока $(\lambda)$") plt.grid()

# Построение теоретического графика производительности plt.figure(figure+1)

plt.plot(lambdas[:9], Q_theoretical[:9], label="Теориетическое Q") plt.plot(lambdas[:9], Q_experimental[:9], label="Экспериментальное

Q")

plt.legend()

plt.title("Оценка результатов моделирования производительности СМО") plt.ylabel("Производительность системы")

plt.xlabel("Интенсивность входного потока $(\lambda)$")

10