lab5

1. Цель работы

Нахождение экспериментальной зависимостей Q(λ, µ₀, N₀) и T(λ, µ₀, N₀) для элементарной системы массового обслуживания с буфером объема N.

Вариант 16

Во втором столбце записан закон распределения входного потока заявок, в третьем – закон распределения времени обслуживания заявок, в четвёртом - µ₀, в пятом - объем буфера N.

2. Ход работы

Записывается формула и строится график экспоненциальный, используемый для распределения заявок на входе. Это представлено на рисунке 1.

Формула: f(x;λ)= λ*e^-λx

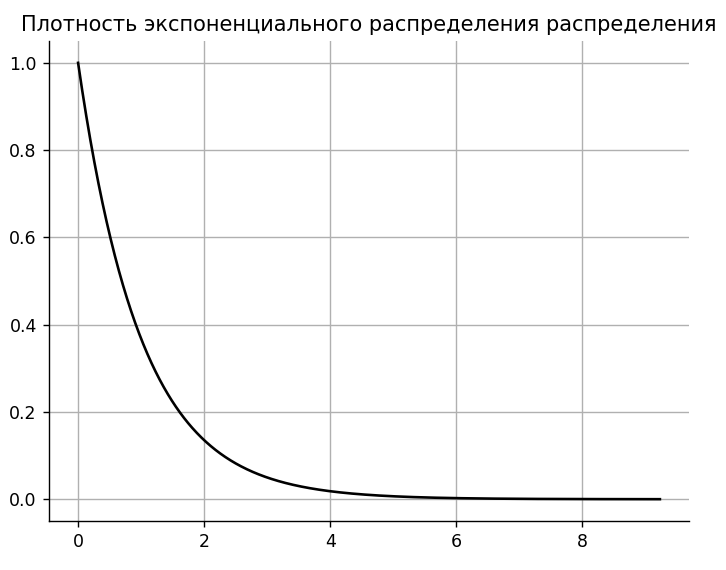
Рисунок 1 – Плотность экспоненциального распределения

Записывается формула и строится график равномерного распределения, используемый для распределения времени обслуживания заявок на выходе. Это представлено на рисунке 2.

Формула: f(x) =

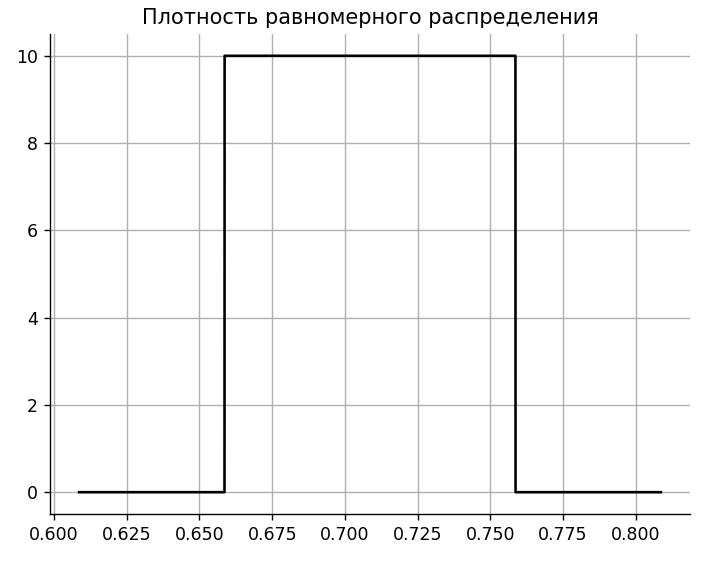
Рисунок 2 – Плотность равномерного распределения

Проводится моделирование работы СМО с буфером. Одним из критериев для вычисления является поиск среднего времени пребывания запроса в системе, которое вычисляется по формуле:

T = * ∑

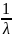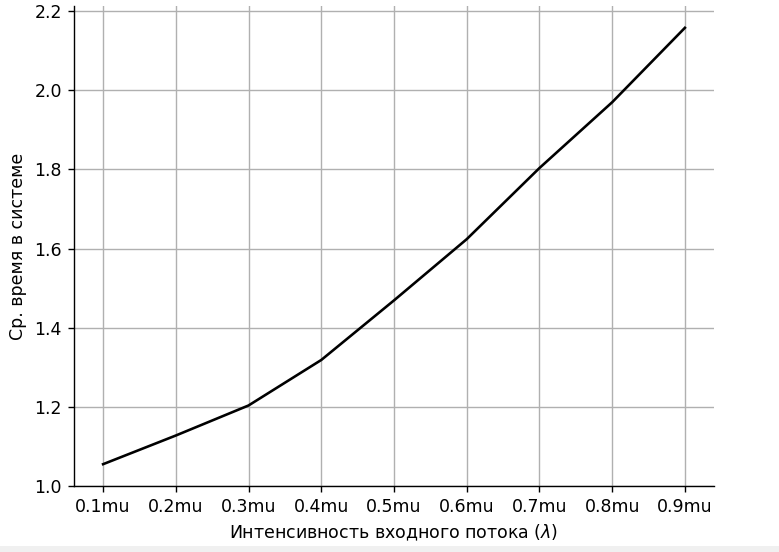
Моделируется работы системы такой системы. Записывается зависимость среднего времени пребывания запроса от интенсивности входного потока. Это представлено на рисунке 3.

.

Рисунок 3 – Моделирование для экспериментальной зависимости среднего времени задержки

При проведении моделирования работы СМО также вычисляется критерий подсчёта производительности такой системы, которая вычисляется по формуле:

Q =

Записывается зависимость производительности от интенсивности входного потока. Это представлено на рисунке 4.

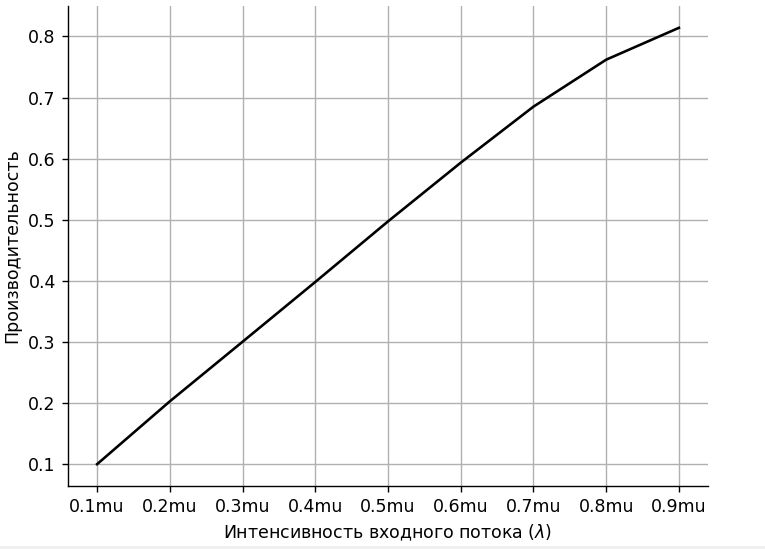
Рисунок 4 – Моделирование для экспериментальной зависимости производительности

Таблица с подробными экспериментальными данными о среднем времени пребывания в системе и средней производительности системы представлена на рисунке 5.

Рисунок 5 - Данные о зависимости среднего времени пребывания запроса от интенсивности входного потока

В программе выполняются моделирования теоретическое и экспериментальное (при заданных по варианту данных) для обоих критериев. График сравнения зависимостей моделирований для среднего времени задержки представлен на рисунке 6. График сравнения зависимостей моделирований для производительности представлен на рисунке 7. При этом погрешность расхождений не превышает 1%. Код выполнения программы представлен в Приложении.

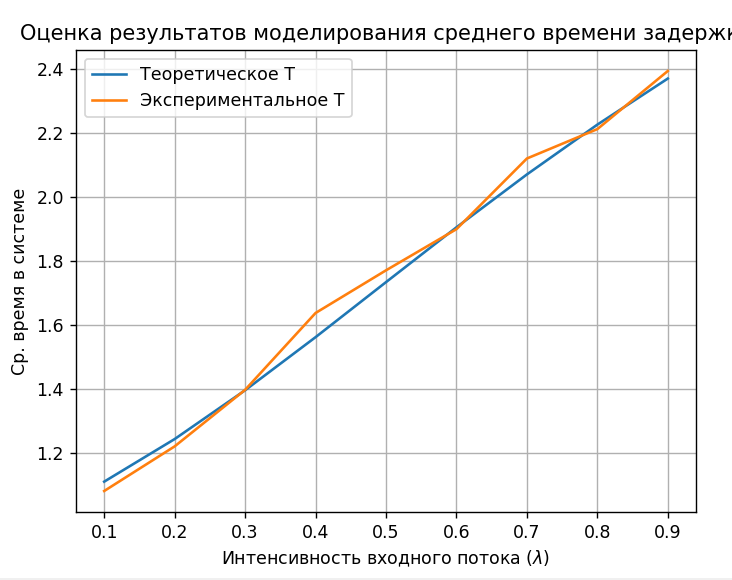
Рисунок 6 – Оценка результатов моделирования среднего времени задержки

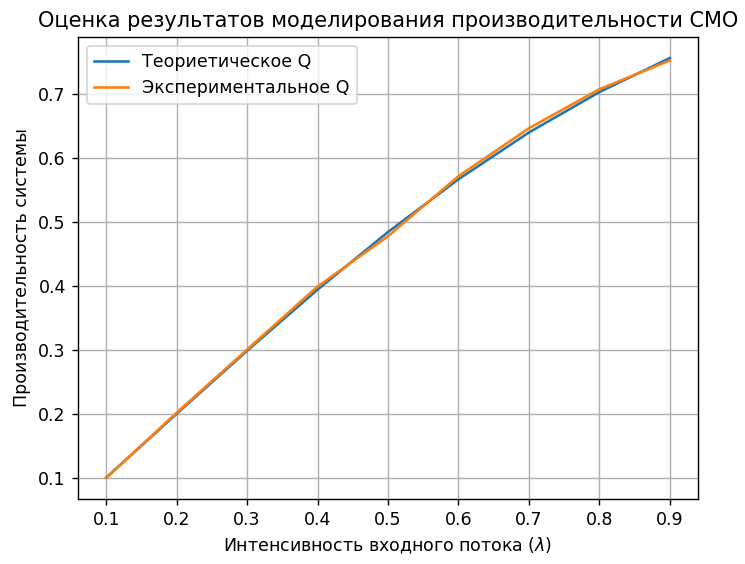
Рисунок 7 – Оценка результатов моделирования производительности

3. Вывод

В ходе данной лабораторной работы я познакомился с элементарной системой массового обслуживания с конечным буфером. В ходе моделирования теоретической и экспериментальной было выяснено, что при увеличении интенсивности входного потока среднее время пребывания в системе сильно увеличивается. При этом, сравнивая среднее время задержки между системами с бесконечным и конечным буфером, сразу заметно, что моделирование такой системы проходит заметно быстрее. Это связано с тем, что при заполнении буфера СМО отбрасывает поступающую заявку, и она просто не будет выполняться. Производительность также возрастает при увеличении интенсивности входного потока. Это значит не только, что нагрузка на систему небольшая, и она вполне справляется с такой работой, но и то, что конечный буфер позволяет системе работать вполне быстро, где заявки не будут долго ждать своей очереди для выполнения.

В ходе работы проблем не возникло.

Приложение

import sys

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from scipy.stats import uniform, expon

def __plot__(figure, arr_x, arr_y=None,

title='', xlabel='', ylabel='',

legend: str = None, color=''):

fig = plt.figure(figure)

ax = fig.add_axes((0.1, 0.1, 0.8, 0.8))

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

if arr_y is None:

ax.plot(arr_x, label=legend, color=color)

else:

ax.plot(arr_x, arr_y, label=legend, color=color)

ax.grid()

ax.set_title(title)

ax.set_ylabel(ylabel)

ax.set_xlabel(xlabel)

if legend is not None:

ax.legend()

def plot_expon_distribution(lambda_, figure):

# Определение границ графика:

temp = expon.rvs(scale= 1/lambda_, size=10000)

x_min, x_max = min(temp), max(temp)

# Построение графика:

x = np.linspace(x_min, x_max, 1000)

y = expon.pdf(x, scale=1/lambda_)

title = 'Плотность экспоненциального распределения распределения'

__plot__(figure, x, y, title, color='black')

def plot_uniform_distribution(a, b, figure):

# Определение границ интервала

x_min, x_max = a - 0.05, b + 0.05

# Построение графика

x = np.linspace(x_min, x_max, 10000)

y = uniform.pdf(x, loc=a, scale=b-a)

title = 'Плотность равномерного распределения'

__plot__(figure, x, y, title=title, color='black')

def model_of_queuing_system(mu, l, is_test, N):

a = 1 / mu - 0.05 * mu

b = a + 0.1 * mu

new_t_income = lambda: expon.rvs(scale=1 / l)

new_t_outcome = lambda: expon.rvs(scale= 1 / mu) if is_test else uniform.rvs(loc=a, scale=b-a)

# системное время

ts = 0

# занятость ОУ

busy = False

# момент поступления заявки

t_in = new_t_income()

t_ins = []

# момент освобождения ОУ

t_out = t_in

t_outs = []

n, k, m = 0, 0, 0

t_mean_old = sys.float_info.max

counter = 0

# производительность

q_mean_old = 2**32

q_data = []

while True:

counter += 1

# Проверяем наступило ли время освобождения ОУ

if t_in <= t_out:

# Записываем в системное время момент поступления заявки

ts = t_in

n += 1 # Увеличиваем счетчик поступивших заявок

# Сохраняем в список момент поступления заявки

# t_ins.append(t_in)

if not busy or m < N:

t_ins.append(t_in)

# Генерируем момент поступления заявки

t_new = new_t_income()

q_data.append(t_new)

# Система обрабатывает сейчас заявку?

if not busy:

busy = True

t_out = ts + new_t_outcome()

elif m < N:

m += 1

# Вычисляем следующий момент поступления заявки

t_in = ts + t_new

else:

# Записываем в системное время момент освобождения ОУ

ts = t_out

k += 1 # Увеличиваем счетчик обслуженных заявок

# Сохраняем в список момент освобождения ОУ

t_outs.append(t_out)

# В буфере больше 0 заявок?

if m > 0:

m -= 1

t_out = ts + new_t_outcome()

else:

busy = False

t_out = t_in

# Ошибка удовлетворительная?

if counter % 1000 == 0:

t_mean_new = np.mean([t_outs[i] - t_ins[i] for i in range(len(t_outs))])

q_mean_new = (k/n) / np.mean(q_data)

if (abs((t_mean_new - t_mean_old) / t_mean_old) < 0.001):

return t_mean_new, q_mean_new

t_mean_old = t_mean_new

q_mean_old = q_mean_new

def experiment(mu, is_test, figure, N):

# Параметры для тестирования

lambdas = np.linspace(0.1, 1, 10) * mu

T_theoretical = []

T_experimental = []

Q_theoretical = []

Q_experimental = []

# Сбор практических данных

for l in lambdas:

t, q = model_of_queuing_system(mu, l, is_test, N)

T_experimental.append(t)

Q_experimental.append(q)

if is_test:

# Сбор теоретических данных

for l in lambdas:

# Подсчёт среднего времени

ro = l / mu

T_theoretical.append(1/l*sum( (i * (1-ro) * ro**i) / (1 -ro**(N+1)) for i in range(N+2) ))

# Подсчёт производительности

Potkl = ((1 - ro)*(ro**N))/(1-ro**(N+1))

Q_theoretical.append(l*(1-Potkl))

# Построение теоретического графика времени

plt.figure(figure)

plt.plot(lambdas[:9], T_theoretical[:9], label="Теоретическое T")

plt.plot(lambdas[:9], T_experimental[:9], label="Экспериментальное T")

plt.legend()

plt.title("Оценка результатов моделирования среднего времени задержки")

plt.ylabel("Ср. время в системе")

plt.xlabel("Интенсивность входного потока $(\lambda)$")

plt.grid()

# Построение теоретического графика производительности

plt.figure(figure+1)

plt.plot(lambdas[:9], Q_theoretical[:9], label="Теориетическое Q")

plt.plot(lambdas[:9], Q_experimental[:9], label="Экспериментальное Q")

plt.legend()

plt.title("Оценка результатов моделирования производительности СМО")

plt.ylabel("Производительность системы")

plt.xlabel("Интенсивность входного потока $(\lambda)$")

plt.grid()

return T_experimental, Q_experimental

if __name__ == "__main__":

mu = 1

a = np.random.random()

b = a + 0.1 * mu

N = 3 # объём буфера

# Построение графиков

plot_expon_distribution(mu, 1)

plot_uniform_distribution(a, b, 2)

print('Проходит моделирование тестовое')

experiment(mu, is_test=True, figure=3, N=3)

print('Проходит моделирование экспериментальное')

index = [rf"{i:.1f}mu" for i in np.linspace(0.1, 1, 10)]

arr1, arr2 = experiment(mu, is_test=False, figure=5, N=3)

df = pd.DataFrame(arr1, index=index, columns=["T"])

df["Q"] = arr2

print(df.T)

# Построение экспериментальных графиков

__plot__(5, df["T"][:9], title='Моделирование для экспериментальной зависимости среднего времени задержки',

ylabel='Ср. время в системе', xlabel='Интенсивность входного потока $(\lambda)$',

color='black')

__plot__(6, df["Q"][:9], title='Моделирование для экспериментальной зависимости производительности',

ylabel='Производительность', xlabel='Интенсивность входного потока $(\lambda)$',

color='black')

plt.show()