ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., канд. техн. наук, доц.				О.О.Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ПРАКТИЧЕСКОЙ РАБОТЕ №2

Исследование метода Монте-Карло для вычисления площадей плоских фигур

по курсу: Производственная (научно-исследовательская работа)

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2023

В ходе выполнения заданий используется вариант №14 и №5.

1. Исследование метода Монте-Карло

В первом задании необходимо исследовать точность метода Монте-Карло на простых фигурах. В моём варианте такая фигура – это правильный шестиугольник со стороной 2. По методу Монте-Карло последовательность действий такова:

1. Сгенерировать случайное число x1 в диапазоне от -r до r, а также случайное число y1 в диапазоне от -r до r. Таким образом, получаем случайную точку с координатами {x1, y1} внутри прямоугольника шириной 2r и высотой 2r. Эта точка может попасть внутрь исследуемой фигуры, а может и не попасть.

2. Проверить принадлежность точки с координатами {x1, y1} к области, площадь которой нужно вычислить. Если попадания нет, т.е. в данном случае при условии y1> sin(x1), то ничего не предпринимаем и переходим к пункту 1, генерируя координаты новой точки {x2, y2}. Если попадание есть, т.е. y1<sin(x1) то необходимо этот факт зафиксировать, инкрементировав предварительно отведенную для этой цели переменную в программе. Попадание точки точно на границу фигуры можно отнести как к первому, так и ко второму исходу — в силу исключительно редкости подобного события, их влияние на результат ничтожно. Код функции, который описывает попадание точки в область шестиугольника, представлен в листинге 1.

Листинг 1 – Код функции, определяющий принадлежность точки к вычисляемой области

function isInside = checkHexagon(x, y)

% Основные параметры шестиугольника

side = 2;

centerX = 0;

centerY = 0;

% Точки по x

verticesX = [

centerX + side * cos(0),

centerX + side * cos(pi/3),

centerX + side * cos(2*pi/3),

centerX + side * cos(pi),

centerX + side * cos(4*pi/3),

centerX + side * cos(5*pi/3)

];

% Точки по y

verticesY = [

centerY + side * sin(0),

centerY + side * sin(pi/3),

centerY + side * sin(2*pi/3),

centerY + side * sin(pi),

centerY + side * sin(4*pi/3),

centerY + side * sin(5*pi/3)

];

% Проверка на принадлежность внутри области

isInside = inpolygon(x, y, verticesX, verticesY);

end

3. Предыдущие пункты повторяются N раз, в данном случае N = 2¹⁶.

4. На каждой итерации вычисляется площадь искомой фигуры, которая зависит от исследуемой области (квадрата размером 2r), количества попаданий и количеством итераций:

S = S_пр

Также вычисляется относительная ошибка вычисления площади фигуры, которая записывается в массив данных, по формуле:

e(N) = 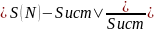*100%

5. Строится график зависимости относительной ошибки от количества итераций на основе пройденных в цикле данных. Результат представлен на рисунке 1.

Основной код цикла и построения графика представлен в листинге 2.

Листинг 2 – Код задания №1

% Сторона шестиугольника

side = 2;

% Радиус шестиугольника

r = (sqrt(3)*side)/2;

% Истинная площадь шестиугольника

S = (3*sqrt(3))/2*side^2;

% Предполагаемая площадь шестиугольника

Spr = (r*2)^2;

% Количество попаданий

P = 0;

% Относительная ошибка

e = [];

% Массив итераций

n = []

% Переменные цикла

N = 1;

endpoint = 2^16;

while N <= endpoint

x = (rand() * 2 * r) - r;

y = (rand() * 2 * r) - r;

if checkHexagon(x,y)

P = P + 1;

end

Sn = Spr * P / N;

e = [e, (abs(Sn-S)/S)*100];

n = [n, N];

N = N + 1;

end

plot(n,e);

title('Зависимость модуля относительной ошибки от N');

xlabel('Количество итераций')

ylabel('Относительная ошибка, %')

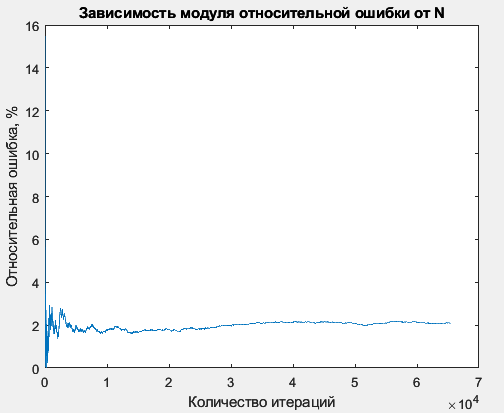
Рисунок 1 – График зависимости модуля относительной ошибки от N

На графике можно увидеть, что первые 15000 операций относительная ошибка постепенно изменяется, далее она статична и находится на уровне 2%, что в принципе допустимо и можно сказать, что метод Монте-Карло работает. Возможно при ещё большем количестве операций, ошибка ещё меньше, но программа при этом будет работать очень долго.

2. Вычисление площади сложной фигуры

В следующем задании необходимо определить площадь сложной фигуры, ограниченной сверху графиком функции y(x) =sin(x), а снизу - графиком функции y(x)=(x-2)^2/2. Для оценки точности также строятся графики функции. Код вычисления и построения графиков представлен в листинге 3, а результаты работы на рисунках 2-3.

Листинг 3 – Код задания №9.2

% Определение функций y(x) = sin(x) и y(x) = (x-2)^2/2

y1 = @(x) sin(x);

y2 = @(x) (x-2).^2 / 2;

% Определение интервала значений x

x = linspace(0, 2*pi, 100);

% Построение графиков двух функций

plot(x, y1(x), 'b', 'LineWidth', 2); hold on;

plot(x, y2(x), 'r', 'LineWidth', 2);

legend('y(x) = sin(x)', 'y(x) = (x-2)^2/2');

xlabel('x'); ylabel('y'); title('Графики функций');

% Вычисление площади фигуры между графиками

area = integral(@(x) abs(y1(x) - y2(x)), 0, 2*pi);

disp(['Площадь фигуры: ', num2str(area)]);

Рисунок 2 – Вычисленная площадь фигуры

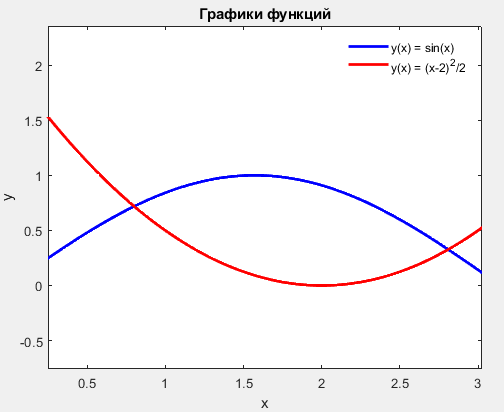
Рисунок 3 – Графики функций, ограничивающих фигуру

Если посчитать, что ограниченная область вписана в прямоугольник площадью 3 (где высота равна 1, а ширина – 3), то полученный ответ вписывается в его рамки, поэтому он правильный.

В ходе выполненных заданий я познакомился с методом Монте-Карло, который с высокой точностью определяет площадь заданной фигуры, а также с другими внутренними функциями программы Matlab: linspace, integral, inpolygon, num2str.

В ходе работы проблем не возникло.