7. Графики, диаграммы и гистограммы

В первом задании необходимо отобразить функцию x(t) = cos(t)*log(t) на отрезке [-1;1] в виде столбчатой диаграммы без промежутков. Код задания представлен в листинге 26, а полученный результат на рисунке 33.

Листинг 26 – Код задания №7.1

t = [-1:0.1:1];

x = cos(t).*log(t);

bar(t,x,1.0)

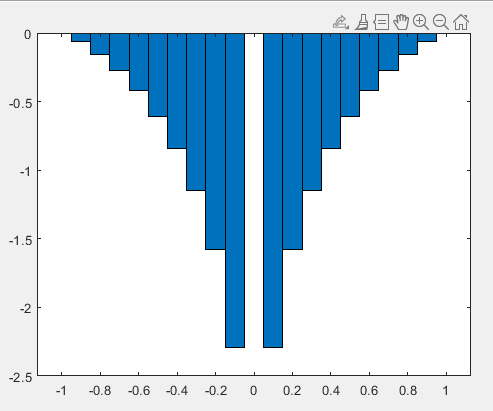
Рисунок 33 – Полученный график к заданию №7.1

Во втором задании необходимо написать команды построения диаграммы с отдельным сектором, соответствующим минимальному значению среди элементов вектора, автоматически создав вспомогательный вектор. Используйте функции zeros для создания нулевого вектора той же длины, что x, и max с двумя выходными аргументами для поиска номера минимального элемента в векторе x. Код задания представлен в листинге 27, а полученный результат на рисунке 34.

Листинг 27 – Код задания №7.2

data = [24.1 17.4 10.9];

parts = zeros(size(data));

[mn, ind] = min(data);

parts(ind) = 1;

pie(data, parts)

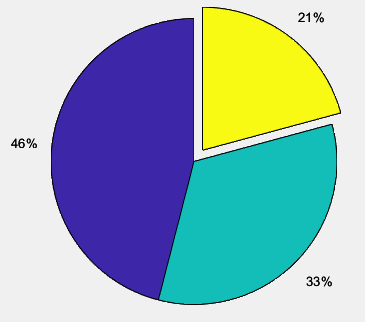
Рисунок 34 – Полученная диаграмма в задании №7.2

Далее необходимо построить диаграмму, где звездочки на горизонтальной оси будут отмечать центры интервалов. Код задания представлен в листинге 28, а полученный результат на рисунке 35.

Листинг 28 – Код задания №7.3

data = [0.9 1.0 1.1 1.2 1.4 2.4 3.0 3.3];

centers = [1.1 2.3 3.2];

hist(data, centers)

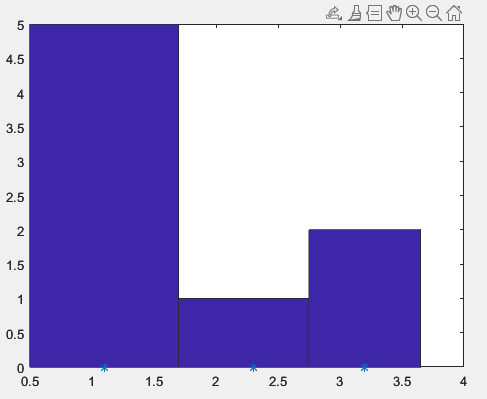
Рисунок 35 – Полученная диаграмма к заданию №7.3

В четвёртом задании необходимо построить графики функций f(x) = e^x/8 cos²(x) и g(x)=6*e^-6x sin²(x) на отрезке [-2π, 2π], а также сгенерировать вектор-строку значений аргумента x и вектор-строку f и g, содержащих значения функций. Код задания представлен в листинге 29, а полученный результат на рисунке 36.

Листинг 29 – Код задания №7.4

x = [-2*pi:pi/20:2*pi];

f = exp(x/8).*cos(x).^2;

g = 6*exp(-6*x).*sin(x).^2;

plot(x,f,x,g)

x1 = [-2*pi:pi/20:0];

x2 = [0:pi/20:2*pi];

f = exp(x1/8).*cos(x1).^2;

g = 6*exp(-6*x2).*sin(x2).^2;

plot(x1, f, x2, g)

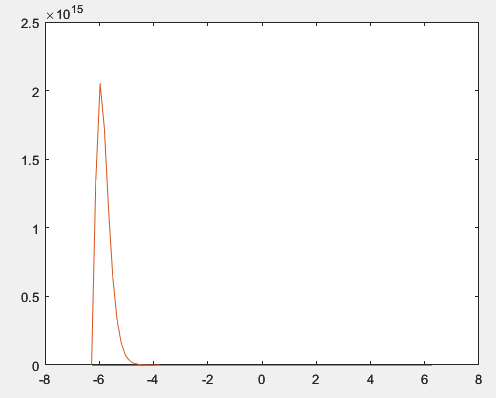
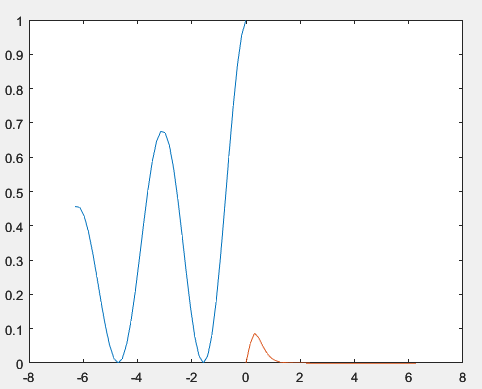
Рисунок 36 – Полученные графики к заданию №7.4

В пятом задании необходимо сравнить две функции: f(x) = 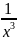и F(x) = 1000*(x+3.5)^-8. Код задания представлен в листинге 30, а полученный результат на рисунке 37.

Листинг 30 – Код задания №7.5

x = [0.5:0.01:3];

f = x.^-3;

F = 1000*(x+3.5.^-8);

plotyy(x,f,x,F)

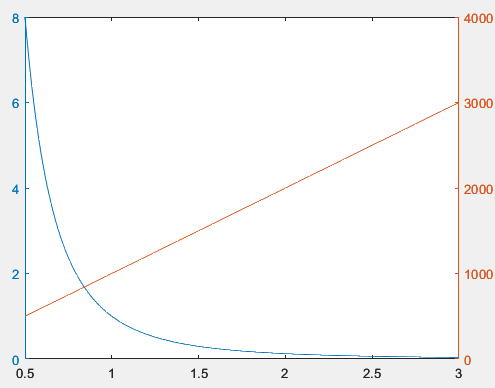
Рисунок 37 – Полученный график к заданию №7.5

Далее необходимо построить графики f(x) = log(0.7x) и g(x) = cos(log(x)) на отрезке [0.1, 5] в логарифмическом масштабе по оси x. Код задания представлен в листинге 31, а полученный результат на рисунке 38.

Листинг 31 – Код задания №7.6

x = [0.1:0.01:5];

f = log(0.7*x);

g = cos(log(x));

semilogx(x,f,x,g)

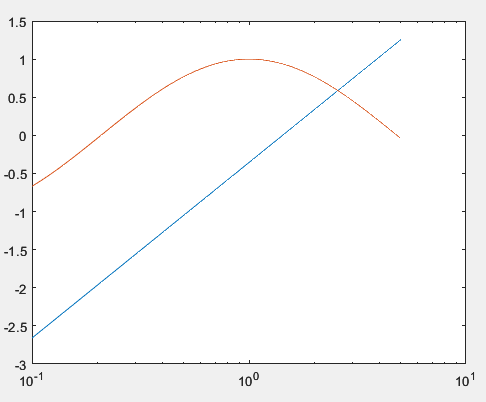
Рисунок 38 – Полученный график к заданию №7.6

Седьмое задание представлено на рисунке 39.

Рисунок 39 – Задание №7.7

Код задания представлен в листинге 32, а полученный результат на рисунке 40.

Листинг 32 – Код задания №7.7

x1 = [-2*pi:pi/20:-pi];

y1 = pi*sin(x1);

x2 = [-pi:pi/20:pi];

y2 = pi - abs(x2);

x3 = [pi:pi/20:2*pi];

y3 = pi*sin(x3).^3;

plot(x1,y1,x2,y2,x3,y3);

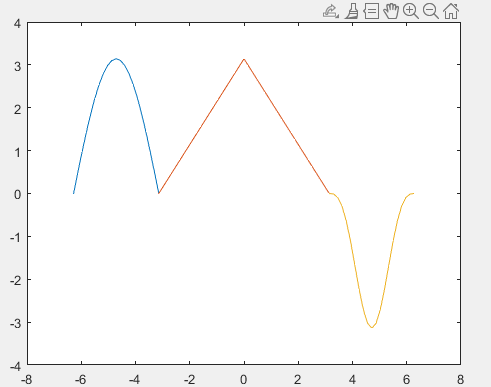
Рисунок 40 – Полученный график к заданию №7.7

Последние два задания представлены на рисунке 41.

Рисунок 41 – Задание №7.8 и 7.9

Код создания графика с прозрачной поверхностью представлен в листинге 33, а полученный результат на рисунке 42.

Листинг 33 – Код графика с прозрачной поверхностью

[X, Y] = meshgrid(-1:0.05:1);

Z = 5*sin(5*pi*X).*X.*cos(8.7*pi).*Y.*(1-X.^2).^Y.*(1-Y);

mesh(X,Y,Z);

hidden off;

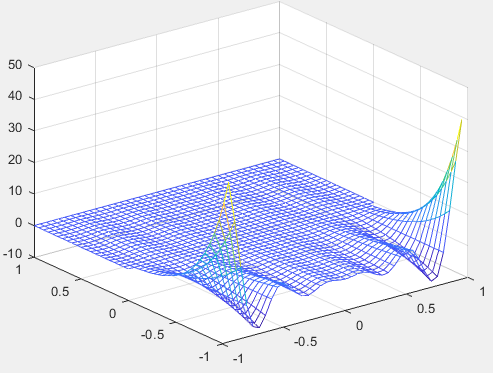
Рисунок 42 – График с прозрачной поверхностью

Код создания графика с непрозрачной поверхностью представлен в листинге 34, а полученный результат на рисунке 43.

Листинг 34 – Код графика с непрозрачной поверхностью

[X, Y] = meshgrid(-1:0.05:1);

Z = 5*sin(5*pi*X).*X.*cos(8.7*pi).*Y.*(1-X.^2).^Y.*(1-Y);

mesh(X,Y,Z);

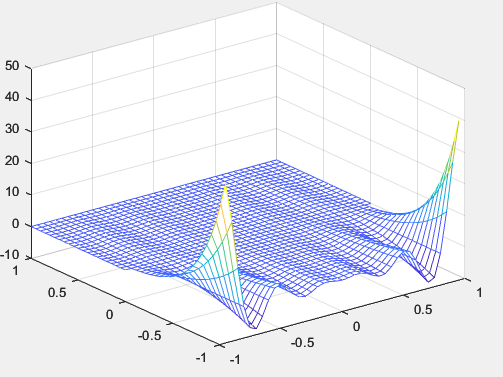
Рисунок 43 – График с прозрачной поверхностью

Код создания графика «c залитыми клетками» в зависимости от значения функции представлен в листинге 35, а полученный результат на рисунке 44.

Листинг 35 – Код графика «с залитыми клетками»

[X, Y] = meshgrid(-1:0.05:1);

Z = 5*sin(5*pi*X).*X.*cos(8.7*pi).*Y.*(1-X.^2).^Y.*(1-Y);

surf(X,Y,Z);

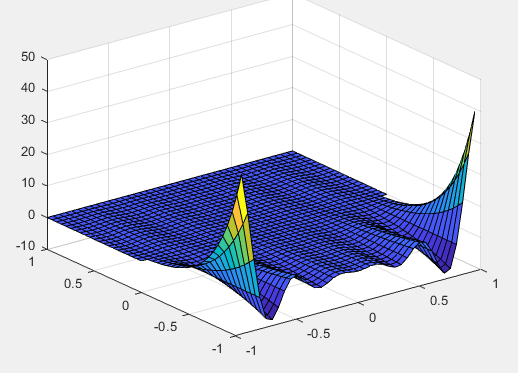
Рисунок 44 – График «с залитыми клетками»

Код графика с поверхностью, плавно залитой цветом, и столбиком, устанавливающим соответствие между цветом и значением функции, представлен в листинге 36, а полученный результат на рисунке 45.

Листинг 36 – Код графика с плавно залитой поверхностью

[X, Y] = meshgrid(-1:0.05:1);

Z = 5*sin(5*pi*X).*X.*cos(8.7*pi).*Y.*(1-X.^2).^Y.*(1-Y);

surf(X,Y,Z);

shading interp;

colorbar

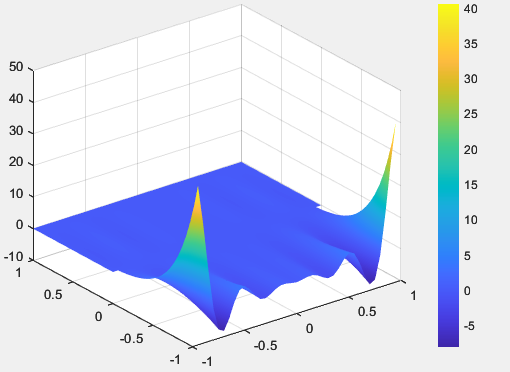
Рисунок 45 – График с плавно залитой поверхностью

Код последнего задания, где на графике необходимо построить поверхностью, которая состоит из линий уровня, соответствующих значениям функции от 0 до 0.5 с шагом 0.08, представлен в листинге 37. Полученный результат на рисунке 46.

Листинг 37 – Код задания №7.9

[X, Y] = meshgrid(-1:0.05:1);

Z = 5*sin(5*pi*X).*X.*cos(8.7*pi).*Y.*(1-X.^2).^Y.*(1-Y);

levels = [0:0.08:0.5];

contour3(X,Y,Z,levels);

colorbar

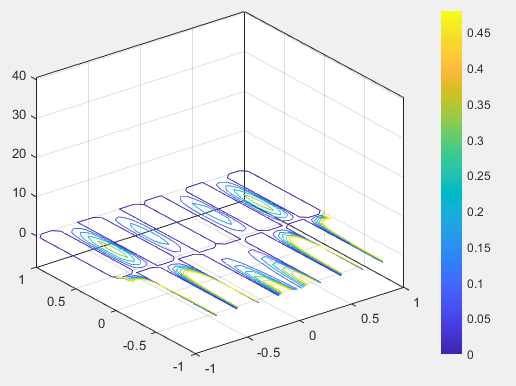
Рисунок 46 – Полученный график к заданию №7.9

В ходе выполненной работы я научился работать с графиками, диаграммами для визуализации определённых функций в Matlab, закрепил базовые навыки владения программой.

8. M-файлы. Численные методы и программирование

В первом задании необходимо написать файл-функцию myfun(с тригонометрическими функциями, степенью, экспонентой, π и квадратным корнем), вычислить значение этой функции в нескольких точках, построить график функции myfun при помощи plot и fplot на одних осях на отрезке [0, 4] из командной строки или при помощи файл программы.

Созданный f-файл представлен в листинге 37, а полученный результат, где ему передаются аргументы x = [1.3 7.2], представлен на рисунке 47.

Листинг 37 – Код файла myfun

function f = myfun(x)

f = exp(-x).*sqrt((x.^2+1)/(cos(x)+2*pi))

Рисунок 47 – Вычисление значений заданной функции в нескольких точках

Код построения графика функции с помощью plot на отрезке [0,4] представлено в листинге 38, а сам график на рисунке 48.

Листинг 38 – Код построения графика функции с помощью plot

x = [0:0.1:4];

y = myfun(x);

plot(x,y)

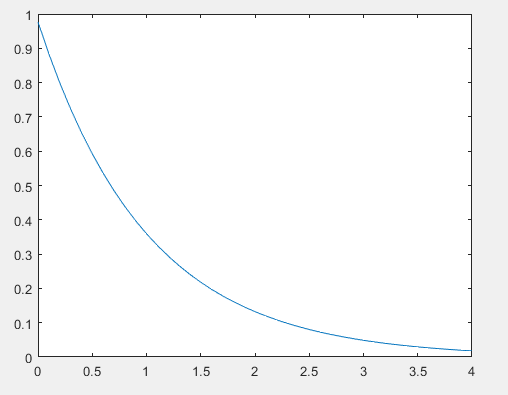
Рисунок 48 – График, построенный с помощью plot (fplot)

Код построения графика с fplot представлен ниже:

fplot('myfun', [0 4])

Результат аналогичен тому, что представлен на рисунке 48.

Во втором задании необходимо решить уравнение 2sin(x)+x²*cos(x)=0 на отрезке [-10; 10], построить график функции и вычислить значения корней уравнения.

Код файла функции представлен в листинге 39. График функции представлен на рисунке 49.

Листинг 39 – Код файла функции к заданию №8.2

function y = myfun(x)

y = sin(x)+x.^2.*cos(x);

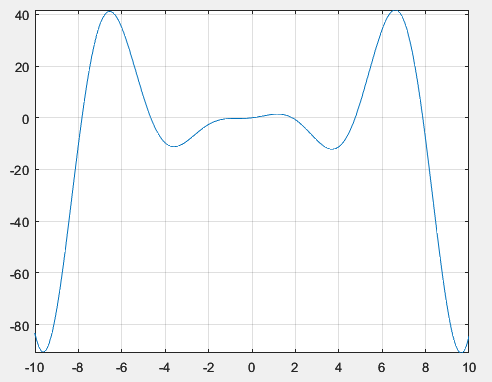
Рисунок 49 – График функции на отрезке [-10;10]

По графику можно увидеть, что уравнение имеет 6 корней, один из которых равен 0. Нахождение остальных пятерых корней представлено на рисунке 50.

Рисунок 50 – Нахождение корней уравнения

В последнем задании необходимо вычислить все корни полинома p=x⁸+6.8x⁷+0.7x⁵+4.5x³-x-8. Код решения представлен в листинге 40, а ответ на рисунке 51.

Листинг 40 – Код задания №8.3

p = [1 6.8 0 0.7 0 4.5 0 -1 -8];

r = roots(p)

Рисунок 51 – Полученный ответ к заданию №8.3

В ходе выполненных заданий я научился создавать функции в отдельных файлах, использовать их на практике, узнал о функции roots для вычисления полиномов, углубил знания работы с Matlab.