2. Вычисление площади сложной фигуры

В следующем задании необходимо определить площадь сложной фигуры, ограниченной сверху графиком функции y(x) =sin(x), а снизу - графиком функции y(x)=(x-2)^2/2. Для оценки точности также строятся графики функции. Код вычисления и построения графиков представлен в листинге 62, а результаты работы на рисунках 63-64.

Листинг 62 – Код задания №9.2

% Определение функций y(x) = sin(x) и y(x) = (x-2)^2/2

y1 = @(x) sin(x);

y2 = @(x) (x-2).^2 / 2;

% Определение интервала значений x

x = linspace(0, 2*pi, 100);

% Построение графиков двух функций

plot(x, y1(x), 'b', 'LineWidth', 2); hold on;

plot(x, y2(x), 'r', 'LineWidth', 2);

legend('y(x) = sin(x)', 'y(x) = (x-2)^2/2');

xlabel('x'); ylabel('y'); title('Графики функций');

% Вычисление площади фигуры между графиками

area = integral(@(x) abs(y1(x) - y2(x)), 0, 2*pi);

disp(['Площадь фигуры: ', num2str(area)]);

Рисунок 63 – Вычисленная площадь фигуры

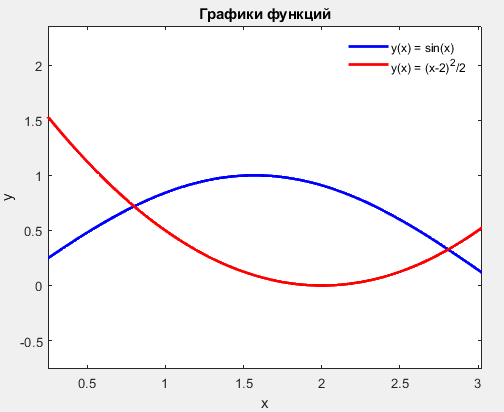
Рисунок 64 – Графики функций, ограничивающих фигуру

Если посчитать, что ограниченная область вписана в прямоугольник площадью 3 (где высота равна 1, а ширина – 3), то полученный ответ вписывается в его рамки, поэтому он правильный.

В ходе выполненных заданий я познакомился с методом Монте-Карло, который с высокой точностью определяет площадь заданной фигуры, а также с другими внутренними функциями программы Matlab: linspace, integral, inpolygon, num2str.

В ходе работы проблем не возникло.

Этап 3. Оценивание функциональных зависимостей методом наименьших квадратов.

В данном задании необходимо изучить метод наименьших квадратов применительно к решению задачи оценивания функциональных зависимостей по выборкам эмпирических данных.

Задание по варианту представлено на рисунке 65.

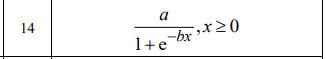
Рисунок 65 – Вариант задания

Здесь задаются параметры функции φ(x), а именно a, b, x_max. Создаётся выборка x, которая получена с помощью датчика случайных чисел с гауссовским распределением. После этого генерируются экспериментальные точки «облака рассеивания» заданной функции с нулевым математическим ожиданием и заданной дисперсией, которые наносятся на график вместе с изначальным графиком. Данные экспериментальных данных записываются в отдельный файл для дальнейшей обработки при вычислении параметров функции. Код представлен в листинге 63, а результат работы на рисунке 66.

Листинг 63 – Код создания функции, её параметров и визуализации

%Задача функции и её параметров

a = 3;

b = 1;

x = [0 7];

x = sort([x (unifrnd(0, 10, 1, 50))]);

y = (a./(1+exp(-b*x)));

%Копирование значений y

y1 = y;

%Зашумление функции

M = 0; %Мат ожидание

D = 0.2; %Дисперсия

for a = 1: 1: length(y)

y1(a) = y1(a) + random('Normal', M, D);

end;

%Выводим график

plot(x,y,x,y1,'*')

title('График начальной функции')

%Запись x и y

res = [];

for i = 1: 1: length(x)

res = [res; [x(i) y1(i)]];

end;

%Записываем результаты в файл

save res.txt res –ASCII

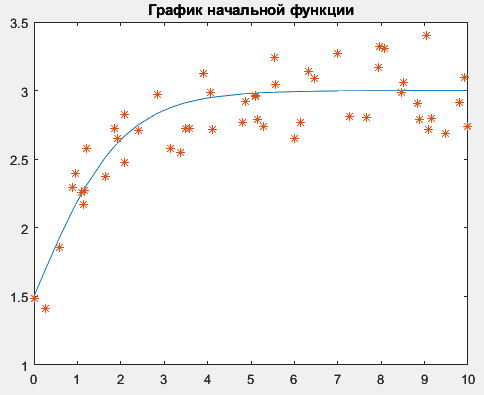
Рисунок 66 – График начальной функции с «облаком рассеивания»

Записанные экспериментальные точки проходят линеаризующее преобразование методом логарифмирования Y_n=ln(y_n) для компенсации экспоненциальной зависимости. После этого подсчитываются элементы системы уравнений после дифференциации уравнения суммы квадратов отклонений, это уравнение записывается в матричном виде, где в результате перемножения можно найти изначальные параметры функции. Строится график по рассчитанным параметрам. Написанный код представлен в листинге 64, а результат на рисунке 67, полученный график на рисунке 68.

Листинг 64 – Код вывода графиков изначальной функции и полученной при помощи МНК

%Запись x,y в массив

Func = load('res.txt');

X = [];

Y = [];

for a = 1: 1: length(Func)

X = [X; Func(a,1)];

Y = [Y; Func(a,2)];

end;

YL = log(Y); %Линеаризующее преобразование

%Решение системы уравнений, её запись в матричном виде

M1 = inv([length(X) sum(X); sum(X) sum(X .^ 2)]);

M2 = [sum(YL); sum(X .* YL)];

%Вычисляем значения параметров функции

S = M1 * M2;

a = S(1); disp(a);

b = S(2); disp(b);

%Вычисление функции по найденным параметрам

y2 = (a./(1+exp(-b*x)));

%Вывод графиков

plot(x,y,'--',x,y1,'*', x, y2);

title('Сравнение графиков начальной функции и МНК-графика')

Рисунок 67 – Вывод параметров функции

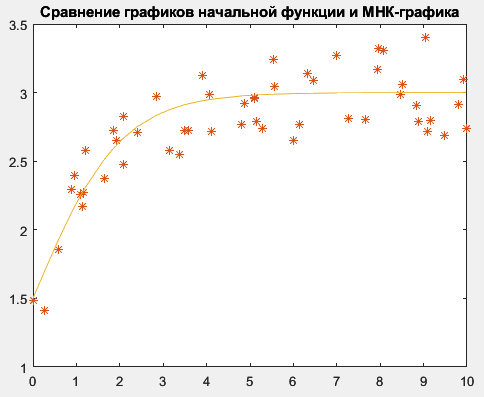
Рисунок 68 – Сравнение графиков изначальной функции и полученной по МНК

Полученные значения a и b почти сходятся с изначально заданным, при этом сравниваемые графики сошлись, это значит, что задание выполнено верно.

Итого в ходе работы я изучил метод наименьших квадратов на примере задачи оценивания функциональных зависимостей по выборкам эмпирических данных, закрепил навыки владения программой Matlab.

В ходе работы проблем не возникло.