9. Программирование. Операторы цикла.

В первом задании необходимо вычислить сумму заданного выражения:

S = ∑ , где k = [1,60]

Код решения представлен в листинге 41, а полученный результата на рисунке 52.

Листинг 41 – Код задания №9.1

x = [pi:pi/4:3*pi];

S = 0;

for k = 1:60

S = S + (exp(k)./(x.^k));

end;

S;

Рисунок 52 – Полученный ответ к заданию №9.1

Во втором задании необходимо написать файл-программу для вычисления выражения Z_x,y = , для x 1, 2, ..., n и y  2, 3, ..., n 1, где пусть n = 30. Код программы представлен в листинге 42, а результат представлен на рисунке 53.

Листинг 42 – Код задания №9.2

S = 0;

n = 30;

for x = 1:n

S = S + ((x+1+x-1)/(x+1-x));

end

S

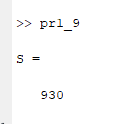
Рисунок 53 – Полученный ответ к заданию №9.2

Последнее задание представлено на рисунке 54.

Рисунок 54 – Задание №9.3

Код файла функции mycos для нахождения суммы ряда для заданного x (разложения в ряд cos(x)) представлен в листинге 43. Сравнение графиков функций mycos и cos на отрезке [ -π, π] на одних осях представлено на рисунке 55.

Листинг 43 – Код файла-функции mycos

function s = mycos(x)

s = 0;

k = 0;

while abs(x.^(5*k)/factorial(5*k))>1.0e-10

s = s + (-1)^k*x.^(5*k)/factorial(5*k);

k = k + 1;

end

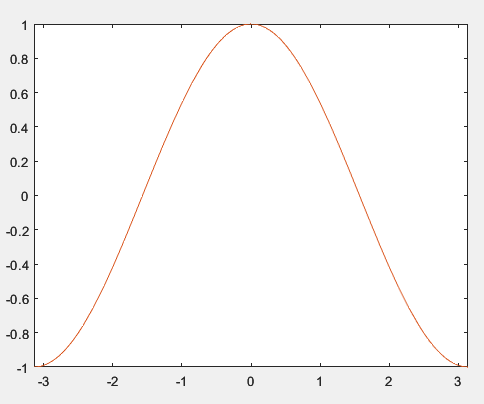
Рисунок 55 – Сравнение графиков mycos и cos

Код файла функции myexp для нахождения суммы ряда для заданного x (разложения в ряд cos(x)) представлен в листинге 44. Сравнение графиков функций myexp и exp на отрезке [ -2π, 2π] на одних осях представлено на рисунке 56.

Листинг 44 – Код файла-функции myexp

function s = myexp(x)

s = 0;

k = 0;

while abs((x.^k)/(factorial(k)))>1.0e-10

s = s + ((x.^k)/(factorial(k)));

k = k + 1;

end

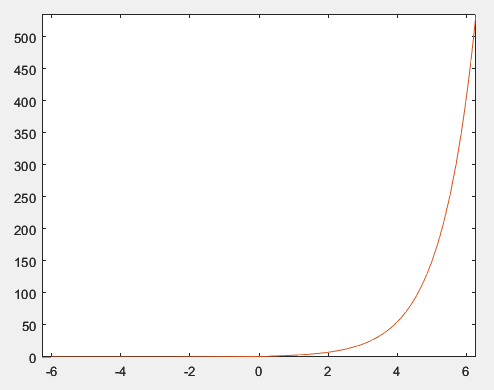
Рисунок 56 – Сравнение графиков myexp и exp

По графику видно, что функции совпадают.

В ходе выполнения работы я научился работать с операторами циклов в Matlab, углубил навыки работы с функциями в программе.

10. Программирование. Операторы ветвления. Исключительные ситуации

В первом задании необходимо написать функцию, которая по коэффициентам квадратного уравнения находит только вещественные его корни, а для комплексных выдает ошибку, при этом функция может принимать на вход только 3 аргумента, а на выходе 2. Также аргументы должны быть действительными числами. Код функции представлен в листинге 45. Пример работы функции представлен на рисунке 57.

Листинг 45 – Код функции root2

function [x1, x2]=root2(a, b, c)

if nargin ~= 3

error('Введите 3 входных аргумента!')

end

if nargout ~= 2

error('Введите 2 выходных аргумента!')

end

[na, ma] = size(a);

[nb, mb] = size(b);

[nc, mc] = size(c);

if na~=1 || ma ~= 1 || nb~=1 || mb ~= 1 || nc~=1 || mc ~= 1

error('Аргументы должны быть числами, а не массивами!')

end

if real(a) ~= a || real(b) ~= b || real(c) ~= c

error('Аргументы должны быть действительными!');

end

d = b^2-4*a*c;

if d<0

error('Уравнение не имеет решения в области действительных чисел!');

end

x1 = (-b-sqrt(d))/(2*a);

x2 = (-b+sqrt(d))/(2*a);

Рисунок 57 – Пример работы функции root2

В листинге 46 представлена функция pwfun1, которая вычисляет кусочно-заданную функцию:

y(x) =

Листинг 46 – Код функции pwfun1

function y = pwfun1(x)

if x < -pi

y = sin(x)-1;

elseif x < pi

y = x / pi;

else

y = -cos(x);

end

Она может принимать на вход и подавать на выход число, вектор-строку, вектор-столбец, матрицу. Примеры использования на рисунке 58.

Рисунок 58 – Работа функции pwfun1

Создаётся функция myplot3D, которая визуализирует придуманную мной трёхмерную функцию:

Z(x,y) = x^y+cos²(y)

Входными аргументами являются границы построения исследуемой функции по каждой из переменных xmin, xmax, ymin, ymax и способ построения графика, определяемый vis: а) построение каркасной поверхности б) построение сплошной поверхности в) построение поверхности с выводом линии уровня г) сплошная поверхность со строением освещенной поверхности.

Все пять входных аргументов проверяются на то, чтобы они были числами, причем xmin меньше xmax и ymin меньше ymax. На основе поданных данных создаются матрицы с координатами узлов сети и значениями функции.

Код функции представлен в листинге 47, а результаты работы на рисунках 59-62.

Листинг 59 – Код функции myplot3D

function myplot3D(xmin, xmax, ymin, ymax, vis)

nxmin = size(xmin);

nxmax = size(xmax);

nymin = size(ymin);

nymax = size(ymax);

if nxmin(2) ~= 1 || nxmax(2) ~= 1 || nymin(2) ~= 1 || nymax(2) ~= 1

error('Аргументы должны быть числами, а не массивами!')

end

if xmin > xmax

error('xmin должен быть больше xmax')

elseif ymin > ymax

error('ymin должен быть больше ymax')

end

if xmin < ymin

if xmax > ymax

[x,y] = meshgrid(xmin:xmax);

else

[x,y] = meshgrid(xmin:ymax);

end

else

if xmax > ymax

[x,y] = meshgrid(ymin:xmax);

else

[x,y] = meshgrid(ymin:ymax);

end

end

z = x.^y + cos(y).^2;

switch vis

case 1

mesh(x,y,z);

case 2

surf(x,y,z);

shading flat;

case 3

levels = 0:0.05:10;

contour3(x,y,z,levels);

colorbar

case 4

surfc(x,y,z);

shading interp;

colorbar;

end

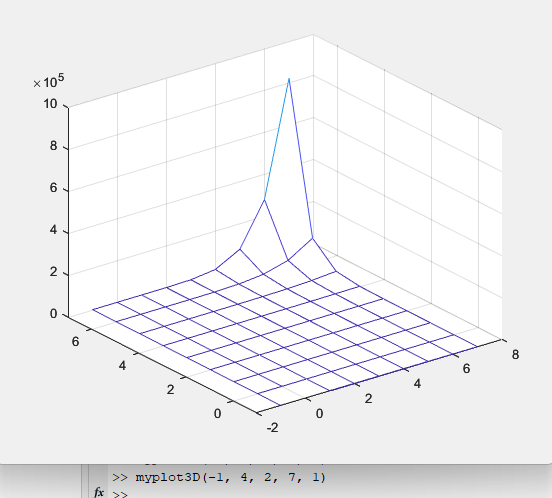
Рисунок 59 – Каркасная поверхность функции

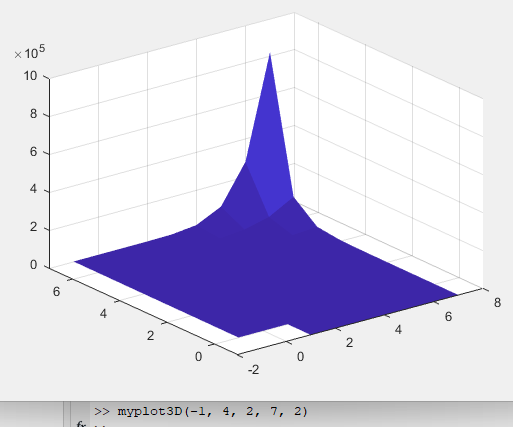
Рисунок 60 – Сплошная поверхность функции

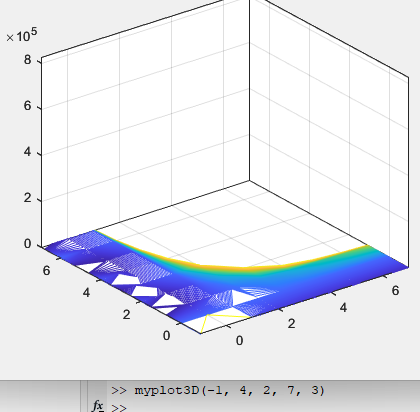
Рисунок 61 – Поверхность функции с линиями вывода

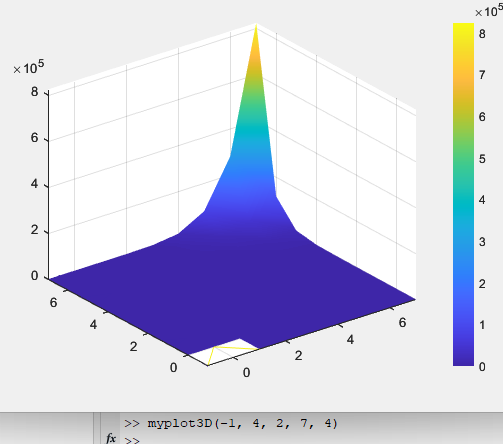
Рисунок 62 – Поверхность функции с цветовой шкалой

В ходе выполненных заданий я познакомился с операторами ветвления if-elseif-else и switch-case в программе Matlab, научился их применять на практике.

Вывод:

В ходе выполненных заданий я познакомился с программой Matlab, познакомился с его базовыми инструментами, а именно:

1. Выполнять простейшие вычисления;

2. Работать с массивами, двумерными массивами, вектор-столбцами, векторами-строками, применять их на практике;

3. Работать с блочными матрицами, визуализировать их и выполнять поэлементные операции над ними;

4. Создавать графики, диаграммы и гистограммы на основе заданных функций;

5. Создавать функции, циклы и условия.

В ходе работы проблем не возникло.