МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА ПРИКЛАДНОЙ ИНФОРМАТИКИ

ОТЧЁТ ПО ПРАКТИКЕ ЗАЩИЩЁН С ОЦЕНКОЙ Руководитель
доц., канд. техн. наук, доц.				О.О.Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЁТ ПО ПРАКТИКЕ

вид практики	Производственная
тип практики	Научно-исследовательская
на тему индивидуального задания		Исследование методов решения задач с
использованием среды MATLAB

выполнен	Жовтяком Максимом Олеговичем
фамилия, имя, отчество обучающегося в творительном падеже

по направлению подготовки	09.03.03		Прикладная информатика
	код		наименование направления
наименование направления
направленности	09.03.03(1)		Прикладная информатика
	код		наименование направленности
в информационной сфере
наименование направленности

Обучающийся группы №	4016				М.О. Жовтяк
	номер		подпись, дата		инициалы, фамилия

Санкт–Петербург 2023

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ

на прохождение производственной (научно-исследовательской) практики обучающегося направления подготовки/ специальности прикладная информатика (09.03.03)

1. Фамилия, имя, отчество обучающегося: Жовтяк Максим Олегович

2. Группа: 4016

3. Тема индивидуального задания:

Исследование методов решения задач с использованием среды MATLAB

4. Исходные данные:

Задание подразумевает выполнение трех этапов: Изучение основ программирования

в среде Matlab; Исследование метода Монте-Карло для вычисления площадей

плоских фигур; Оценивание функциональных зависимостей методом наименьших

квадратов. Варианты заданий приведены в методических указаниях.

5. Содержание отчетной документации:

1. индивидуальное задание;

2. отчёт, включающий в себя:

• титульный лист;

• материалы о выполнении индивидуального задания (содержание определяется кафедрой);

• выводы по результатам практики;

• список использованных источников.

3. отзыв руководителя от профильной организации (при прохождении практики в профильной организации).

6. Срок представления отчета на кафедру: «24» августа 2023

Руководитель практики

доц., канд. техн. наук, доц. О.О.Жаринов

должность, уч. степень, звание подпись, дата инициалы, фамилия

СОГЛАСОВАНО

Руководитель практики от профильной организации

должность подпись, дата инициалы, фамилия

Задание принял к исполнению

обучающийся

М.О. Жовтяк

дата подпись инициалы, фамилия

Санкт–Петербург 2023

В ходе выполнения заданий используется вариант №14 и вариант №5 (во втором этапе).

Этап 1. Изучение основ программирования в среде matlab

1. Простейшие вычисления в Matlab

Необходимо вычислить выражение, представленное на рисунке 1, на Matlab одной строкой. Код представлен в листинге 1, а ответ на рисунке 2.

Рисунок 1 – Задание №1.1

Листинг 1 – Код задания №1.1

((sqrt(5*cot(4.8))-sin(1.3*pi))/(cos(2.7*pi)+(log(25.2))^3))-sqrt(log(15.5))*(1-exp(2/5))

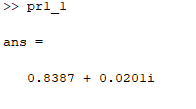
Рисунок 2 – Полученный ответ к задаче №1.1

Теперь надо вычислить похожее выражение, но уже используя присвоение переменных, что намного облегчает читаемость кода. Задание представлено на рисунке 3, код в листинге 2, а ответ на рисунке 4.

Рисунок 3 – Задание №1.2

Листинг №2 – Код задания №1.2

x = (cos(5.9*pi)/sin(3.8*pi))^2;

y = (tan(2.56)/cos(4.4*pi));

z = (log(3.2)/(8*log(7.3)));

a = (cos(9.2*pi)/sin(6.6*pi));

b = sqrt(tan(7.26)/cos(5.4*pi));

(x-y+z)/(a+b)

Рисунок 4 – Полученный ответ к заданию №1.2

В результате выполнения этих задач я приобрёл базовые знания о математических вычислениях в Matlab.

2. Работа с массивами. Векторы-столбцы и векторы-строки

В ходе первого задания необходимо вычислить сумму векторов, которые представлены на рисунке 5.

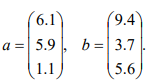
Рисунок 5 – Задание №2.1

Код представлен в листинге 3, ответ на рисунке 6.

Листинг 3 – Код задания №2.1

a = [6.1;5.9;1.1];

b = [9.4;3.7;5.6];

c = a+b

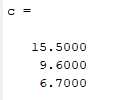
Рисунок 6 – Полученный ответ к заданию №2.1

Далее необходимо вывести пятый элемент вектора-строки v = (1.5 1.2 8.5 1.7 2.4),заменить второй элемент вектора-строки на 1.1, записать в массив w второй, пятый и первый элементы. Код представлен в листинге 4, ответ на рисунке 7.

Листинг 4 – Код задания №2.2

disp('Пункт 1')

v = [1.5;1.2;8.5;1.7;2.4];

disp(v(5));

disp('Пункт 2')

v(2) = 1.1;

disp(v)

disp('Пункт 3')

w = [v(2);v(5); v(1)];

disp(w)

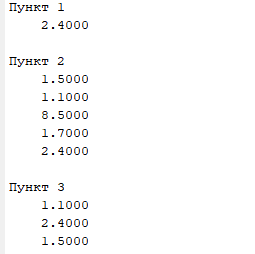
Рисунок 7 – Полученный ответ к задаче №2.2

В следующем задании необходимо в массиве вектора-строки w = (4.4 5.3 6.5 7.8 2.9 0.7 2.1) заменить нулями элементы со второго по шестой; создать новый массив w1, используя элементы массива w с третьего по седьмой и составить массив w2,содержащий элементы w, кроме четвертого (используя сцепление строк). Код представлен в листинге 5, результат на рисунке 8.

Листинг 5 – Код задания №2.3

% Первый пункт

w = [4.4;5.3;6.5;7.8;2.9;0.7;2.1];

w(2:6) = 0;

disp(sprintf('%g ', w'));

% Второй пункт

w1 = w(3:7);

disp(sprintf('%g ', w1'));

% Третий пункт

w2 = [w(1:3);w(5:7)];

disp(sprintf('%g ', w2'));

Рисунок 8 – Полученный ответ к заданию 2.3

Четвёртое задание представлено на рисунке 9.

Рисунок 9 – Задание №2.4

Код к решению этого задания представлен в листинге 6, а ответ на рисунке 10.

Листинг 6 – Код задания №2.4

% Первый пункт

z = [5.5;2.9;9.7;1.6;6.1;5.1];

disp(prod(z));

% Второй пункт

[M,k] = max(z);

m = min(z);

disp(M);

disp(m);

disp(k);

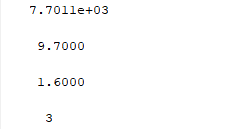
Рисунок 10 – Ответ к заданию №2.4

Далее необходимо упорядочить вектор-строку r = (–6.4 3.3 0.9 –1.2 5.2 3.5):

а) по возрастанию;

б) по убыванию;

в) в порядке возрастания их модулей;

г) по возрастанию с двумя выходными аргументами (это приведет к образованию массива индексов соответствия элементов упорядоченного и исходного массивов).

Код решения представлен в листинге 7, а результат на рисунке 11.

Листинг 7 – Код задания №2.5

r = [-6.4;3.3;0.9;-1.2;5.2;3.5];

R = sort(r);

disp(sprintf('%g ', R'));

R1 = sort(r,'descend');

disp(sprintf('%g ', R1'));

R2 = sort(abs(r));

disp(sprintf('%g ', R1'));

[rs, nd] = sort(r);

disp(sprintf('%g ', rs'));

disp(sprintf('%g ', nd'));

Рисунок 11 – Полученный ответ к заданию №2.5

В последнем задании необходимо:

а) Перемножить векторы-строки v1 = (8 4 7 –1) и v2 = (–3 2 –4 5);

б) возвести во вторую степень вектор v1;

в) все элементы первого вектора v1 возвести в степень, равную соответствующим элементам второго вектора v2;

г) разделить вектор v1 на v2 и v2 на v1;

д) к вектору-строке v= (5 2 8 4) прибавить число 9.4, вычесть его из вектора, умножить вектор v на число 2 и разделить на это же число. Код представлен в листинге 8, все результаты на рисунке 12.

Листинг 8 – Код задания №2.6

v1 = [8;4;7;-1];

v2 = [-3;2;-4;5];

u = v1 .* v2;

disp(sprintf('%g ', u'));

p = v1.^2;

disp(sprintf('%g ', p'));

P = v1.^v2;

disp(sprintf('%g ', P'));

d1 = v1./v2;

disp(sprintf('%g ', d1'));

d2 = v2./v1;

disp(sprintf('%g ', d2'));

v = [5;2;8;4];

s = v + 9.4;

disp(sprintf('%g ', s'));

r1 = v - 9.4;

disp(sprintf('%g ', r1'));

p1 = v * 3;

disp(sprintf('%g ', p1'));

p2 = v / 3;

disp(sprintf('%g ', p1'));

Рисунок 12 – Полученный ответ к заданию №2.6