lab4_IO_Zhovtyak

Цель работы

Изучить процесс решения различных задач на основе матриц игр.

Вариант

Вариант – 14, показан на рисунке 1.

Рисунок 1 – Условия по варианту

Ход работы

Были найдены верхняя и нижняя цена игры, изображённой на рисунке 2.

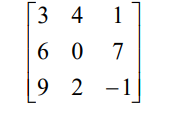
Рисунок 2 – Матрица для нахождения цен игры

Минимальные значение строк: 1, 0, -1. Наибольшее из них – 1. Данное значение равно нижней цене игры.

Максимальные значения столбцов: 9, 4, 7. Наименьшее из них – 4. Данное значение равно верхней цене игры.

Согласно полученным результатам, нижняя цена игры – 1, что говорит минимальном выигрыше A, если он будет придерживаться максимальной стратегии; верхняя цена игры – 4, что говорит о максимальном проигрыше со стороны B, если он будет придерживаться наиболее осторожной стратегии. Так как значения не равны, то седловой точки нет, то нет и решений в чистых стратегиях.

Было найдено решение в смешанных стратегиях математической матрицы, изображённой на рисунке 3, аналитически.

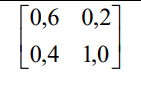
Рисунок 3 – Матричная игра 2x2

Были найдены оптимальные стратегии и цена игры: x^*T= y^*T=[0.8 0.2]; v=0.52.

Оптимальная стратегия была найдена при помощи понятия равновесия Нэшу.

x^*T= y^*T=[0.8 0.2];

Было проведено сокращение размерности игры, изображённой на рисунке 4, до вида m*2.

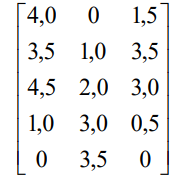
Рисунок 4 – Исходная матрица

Необходимо убрать невыгодные стратегии.

Все значения А3 больше, чем А1. При нахождении невыгодных стратегий для игрока А (строки) убираются строки с меньшим выигрышем. Поэтому, строка А1 удаляется.

Все значения В1 больше, чем В3. При нахождении невыгодных стратегий для игрока В(колонки) убираются колонки с наибольшими значениями (выигрыш игрока А). Поэтому, В1 удаляется. Полученная матрица показана на рисунке 5.

Рисунок 5 – Преобразованная в вид m*2 матрица

На рисунке 6 показана графическая интерпретация задачи нахождения решения игры в смешанных стратегиях.

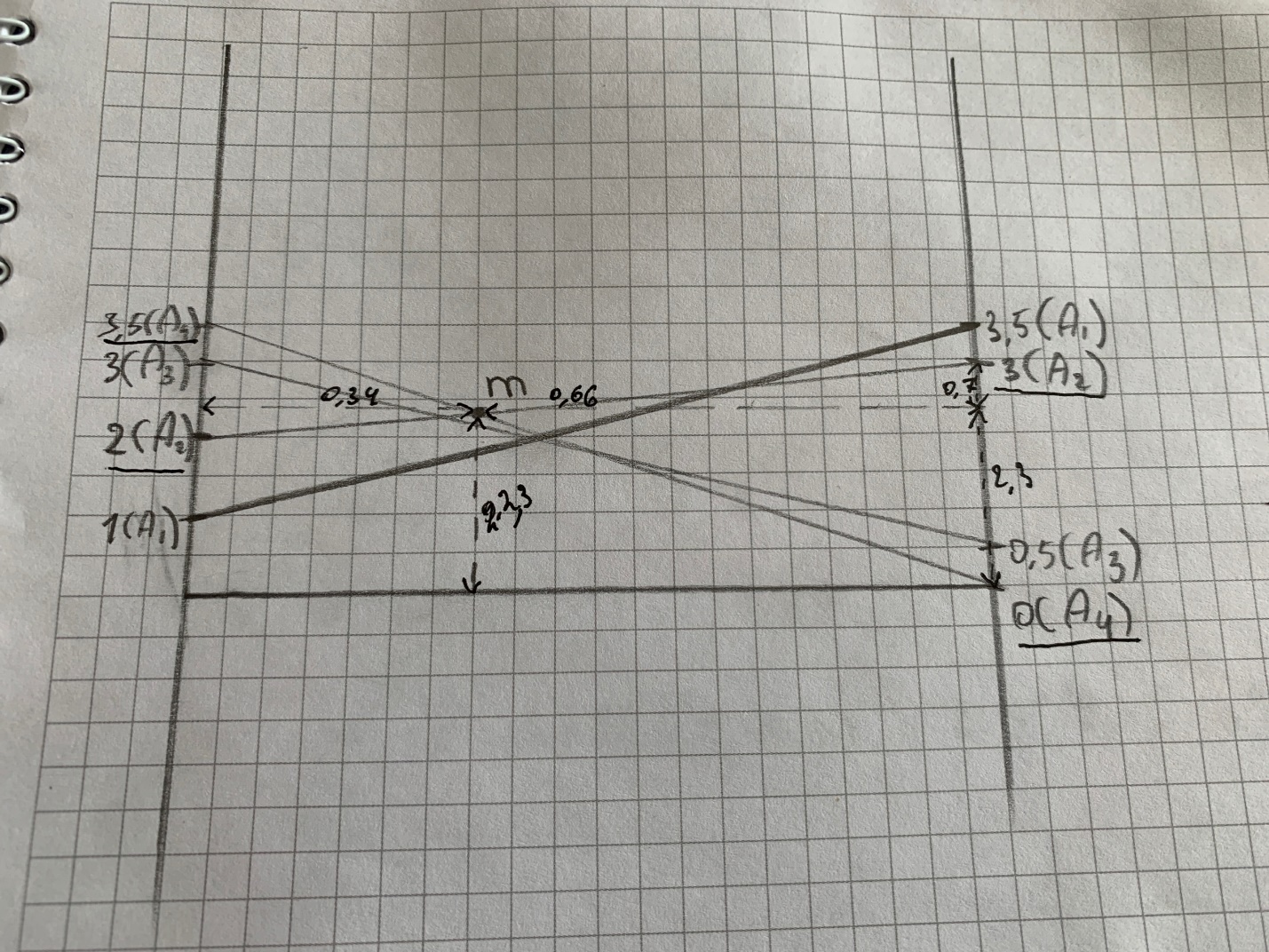
Рисунок 6 – Графическая интерпретация

По построению значения:

1. Цена игры v = 2.3 (расстояние до нулевой линии);

2. Оптимальная смешанная стратегия для игрока В y^*T=[0.66 0.34] (расстояние до правой и левой границ);

3. x₄=

4. x₂=1-x₄=1-0.23=0.77;

5. Оптимальная смешанная стратегия для игрока А x^*T=[0 0.77 0 0.23].

На рисунке 7 показано решение задачи в Excel. Значения близки, что говорит о верном расчете.

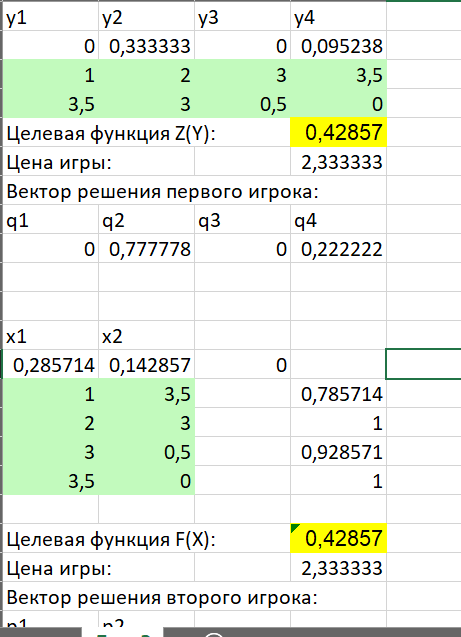
Рисунок 7 – Решение в Excel

Вывод

Была проанализована матрица игры. Были определены ее решения в чистых стратегиях и цена. Было найдено решение в смешанных стратегиях матричной игры 2х2. Было проведелено сокрашение размерности игры до m*2. Аналитически и в среде Excel было найдено решенние в смешанных стратегиях для полученной сокрешаенной игры m*2.