
lab3_IO_Zhovtyak
.docx
 Цель
работы
Цель
работы
Найти решение задачи эвакуации и задачи распределения ресурсов.
Вариант
Вариант – 14. Задание показано на рисунке 1.

Рисунок 1 – Условия по варианту
Ход работы
Вручную была посчитана задача эвакуации. На таблице 1 показано итоговое решение задачи, на таблице 2 – предварительная оптимизация, на таблицах 3-4 – примеры промежуточных расчетов для ячеек.
Таблица №1
Решение задачи эвакуации
-
П1
П2
П3
П4
g (вес)
2
3
4
4
C (цена)
30
35
40
50
x
1
0
1
1
Таблица предварительной оптимизации заполнялась следующим образом: предметы были расположены на эвакуацию в обратном порядке, чтобы самый маленький вес был в последней колонке; в последней колонке оставляем только две последние строки (так как вес П1 равен 2), так как подразумевается, что все ячейки мест выше уже заняты; таблица заполнялась слева на право; для каждого предмета, в зависимости от его цены и веса, было принято решение брать его или нет.
Ход решения:
1. Предмет 4 имеет вес 4 и цену 50. Следовательно, мы не можем его взять, пока доступная грузоподьемность (S) меньше, чем 4. При S равном 4 возможно взять предмет, поэтому в решение (x4) записывается 1 (берем), в общую ценность (ω4) цена предмета 50. При увеличении S предмет все также возможно взять.
2. Предмет 3 имеет вес 4 и цену 50. Следовательно, его можно взять только при S равном 4. Однако, в прошлой колонке при S равном 4 уже есть значение (предмет П4 взят). Так как места при S равном 4 только 4, то нужно определить, что выгодней взять – П3 или П4. П3 имеет цену лишь 40, а А4 50 – выгоднее взять П4. При этом, цена на данный момент будет равна цене взятого товара П4 (50) При увеличении S увеличивается и доступное место (при S = 5, раз берем П4, то свободно будет одно место) – следовательно, при S равном 8 будет уже 4 свободных мест (берем П4, который весит 4. 8-4=4). Таким образом, при s равном 8 можно взять предмет П3. Тогда цена на данный момент (ω3) будет равен весу П3+П4=40+50=90.
3. Предмет 2 имеет вес 3 и цену 35. Заполнение происходит аналогичным прошлому способу. Так, при 4 свободных местах данный товар не выгодно брать, а при 7 можно взять и П4 и П2. При s равном 8 уже нужно решить, что выгодней П4+П3 (90) или П4+П2(85). Первый вариант выгоднее, поэтому П2 не взят.
4. Предмет 1 весит 2 и стоит 30. Для определения берем\не берем применялась вспомогательная таблица (таблицы 3-4), так как вариантов прошлых действий достаточно много. В вспомогательной таблице мы рассматриваем два варианта: берем (x = 1) или не берем(x= 0). Также указываем цену (если берем, то она равна 30, если нет, то 0). После этого указываем какой вес из прошлой колонки доступен (когда проверяем s=9, то если не берем, то просматриваем прошлую колонку со значением 9, если берем, то доступный вес уменьшается и просматриваем уже 9-2=7 колонку). В следующем столбце указываем цену из прошлой колонки таблицы оптимизации при найденных S. В последней колонке вспомогательной матрице просто скалываем X1C1 и ω2 – где значение больше, то решение и принимаем.
5. Выделяем последнюю строку последнего столбца. Видим, что принято решение брать П1. П1 весит 2, поэтому дальше выделяем 10-2-8 строку. Видим, что принято решение не брать П2, поэтому просматриваем туже строку столбца для П3. Видим, что принято решение брать П3. Просматриваем столбец для П4 8-4=4. Выделяем клетку. Выделение клетки показывают решение – берем или не берем.
Таблица №2
Таблица предварительной оптимизации
-
S
П4
П3
П2
П1
x4
ω4
x3
ω3
x2
ω2
x1
ω1
1
0
0
0
0
0
0
2
0
0
0
0
0
0
3
0
0
0
0
1
35
4
1
50
0
50
0
50
5
1
50
0
50
0
50
6
1
50
0
50
0
50
7
1
50
0
50
1
85
8
1
50
1
90
0
90
9
1
50
1
90
0
90
1
115
10
1
50
1
90
0
90
1
120
Таблица №3
Пример промежуточных расчетов
X1 |
X1C1 |
S2 |
ω2 |
ω1 |
1 |
30 |
7 |
85 |
115 |
0 |
0 |
9 |
90 |
90 |
Таблица №4
Пример промежуточных расчетов
X1 |
X1C1 |
S2 |
ω2 |
ω1 |
1 |
30 |
8 |
90 |
120 |
0 |
0 |
10 |
90 |
90 |
Согласно полученным результатам, эвакуации подлежат: П1, П3 и П4.
Задача распределения ресурсов была при помощи программных средств. На рисунке 2 показана исходная задача, подаваемая в виде матрицы. Ответ, полученный на основе составленного кода, показан на рисунке 3.
Краткое описание кода: на основе имеющихся и получаемых значений образуются список для всех списков x и ω (рисунок 4). По итогу, если списки рассматривать вместе, то получаем ту же таблицу, что строили на лекции. После этого, подобно тому, как выбирали итоговое решение в таблице 2, выделяем решения в ней. После этого возвращаемся к исходной задаче (рисунок 1) и смотрим, какие значения для каждого П на выбранных местах x.

Рисунок 2 – Исходная задача

Рисунок 3 – Ответ на задачу распределения
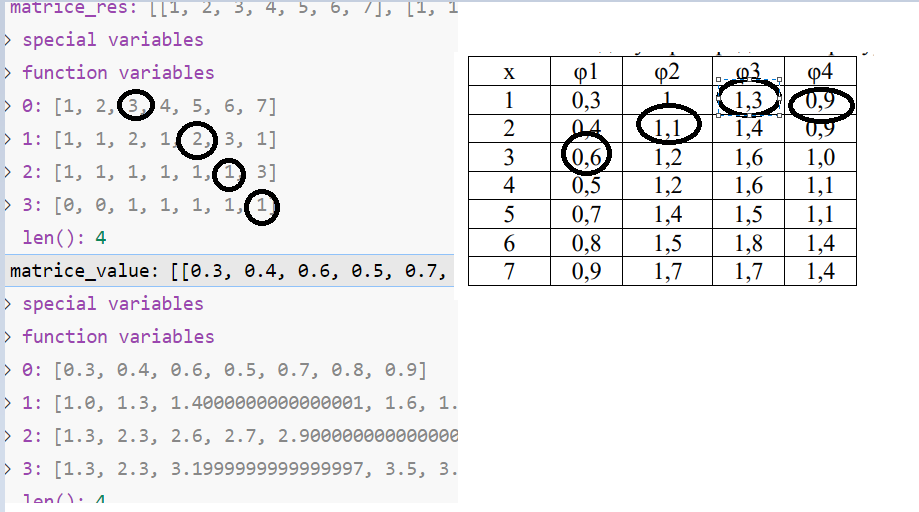
Рисунок 4 – Значение списков x и ω и решение по ним
Листинг. Решение задачи распределения ресурсов
def mision_ressources(tableau):
#В матрице результатов значения матрицы перевернуты
matrice_res=[]
matrice_value=[]
for i in range(len(tableau[0])):
mass_res_une=[]
mass_res_une2=[]
for j in range(len(tableau)):
mass_res_une.append(0)
mass_res_une2.append(0)
matrice_res.append(mass_res_une)
matrice_value.append(mass_res_une2)
#Матрица значений результатов
#Заполняем первую строку
for i in range(len(matrice_res[0])):
matrice_value[0][i]=tableau[i][0]
matrice_res[0][i]=i+1
#Заполняем прочие строки
for i in range(1,len(matrice_res)):
for j in range(len(matrice_res[i])):
table_help=[]
#Создаем вспомогательную таблицу. число строк -
for k in range(j+2):
table_help_une=[]
for s in range(5):
table_help_une.append(0)
table_help.append(table_help_une)
#Заполняем полученную таблицу
for k in range(len(table_help)):
table_help[k][0]=k
if k!=0:
table_help[k][1]=tableau[k-1][i]
table_help[k][2]=len(table_help)-(k+1)
if table_help[k][2]!=0:
table_help[k][3]=matrice_value[i-1][table_help[k][2]-1]
table_help[k][4]=table_help[k][1]+table_help[k][3]
#Находим максимальный элемент
max=0
for k in range(len(table_help)):
if table_help[k][4]>max:
max=table_help[k][4]
max_index=k
matrice_value[i][j]=max
matrice_res[i][j]=max_index
#Создаем массив с выбраными φ
mass_res=[]
S=len(matrice_value[i])-1
for i in range(len(matrice_value)):
mass_res.append(matrice_res[len(matrice_value)-i-1][S])
S=S-matrice_res[len(matrice_value)-i-1][S]
mass_res=list(reversed(mass_res))
victoire=0
for i in range(len(mass_res)):
t=tableau[mass_res[i]-1][i]
victoire=victoire+tableau[mass_res[i]-1][i]
return(mass_res,round(victoire,2))
tabl=[[0.3,1.0,1.3,0.9],
[0.4,1.1,1.4,0.9],
[0.6,1.2,1.6,1.0],
[0.5,1.2,1.6,1.1],
[0.7,1.4,1.5,1.1],
[0.8,1.5,1.8,1.4],
[0.9,1.7,1.7,1.4]]
res,victoire = mision_ressources(tabl)
print('Максимальный доход - ', victoire)
print('При распределении - ', res)
Вывод
В ходе работы были изучен процесс решения задачи эвакуации и задачи распределения ресурсов.
