
lab1_IO_Zhovtyak
.pdf
1

1. Задание
Решить задачу линейного программирования графическим методом и аналитически - симплекс-методом. Проверить решение c помощью Excel.
Сформулировать задачу, двойственную к заданной, решить, сравнить результаты.
Вариант 14:
{
2. Графический метод
Система неравенств была решена графически, а именно, построена область допустимых значений. Р
Рисунок 1 – Область допустимых значений
2
На данном рисунке красным цветом представлена область значений первого неравенства, синим – второго и зелѐным – третьего. Желтой замкнутой линией обозначена общая область допустимых значений.
Чтобы целевая функция стремилась к минимум, нужно, чтобы оба значения были максимально большими. Изучим значение целевой функции при нахождении в точках A, B, C соответственно:
A)L(x) = (-2 * 0) + (-3*3) = -9.
B)L(x) = (-2 * 3) + (-3*2) = -12.
C)L(x) = (-2 * 5) + (-3*0) = -10.
Под эти критерии идеально подходит точка B(3,2), в ней целевая функция равна -12 – минимальному из всех значений.
3. Симплекс-метод
Преобразуем неравенство в уравнение, введя базисные перемене x3, x4, x5:
{
Составляем таблицу.
Базис |
План |
X1 |
X2 |
X3 |
X4 |
X5 |
Ѳ |
|
|
|
|
|
|
|
|
X3 |
15 |
3 |
3 |
1 |
0 |
0 |
15/3 |
|
|
|
|
|
|
|
|
X4 |
9 |
1 |
3 |
0 |
1 |
0 |
9/3 |
|
|
|
|
|
|
|
|
X5 |
-4 |
0 |
1 |
0 |
0 |
1 |
4/1 |
|
|
|
|
|
|
|
|
L |
0 |
2 |
3 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
Минимальное значение Ѳ равно 3, следовательно, 2-я строка является
ведущей. Разрешающий элемент равен 3 и находится на пересечении
3
ведущего столбца и ведущей строки. Формируем новую симплекс-таблицу,
заменой X4 на X2:
Базис |
План |
X1 |
X2 |
X3 |
X4 |
X5 |
Ѳ |
|
|
|
|
|
|
|
|
X3 |
6 |
2 |
0 |
1 |
-1 |
0 |
3 |
|
|
|
|
|
|
|
|
X2 |
3 |
1/3 |
1 |
0 |
1/3 |
0 |
9 |
|
|
|
|
|
|
|
|
X5 |
1 |
-1/3 |
0 |
0 |
-1/3 |
1 |
- |
|
|
|
|
|
|
|
|
L |
-9 |
1 |
0 |
0 |
-1 |
0 |
|
|
|
|
|
|
|
|
|
Минимальное значение Ѳ равно 3, следовательно, 1-я строка является ведущей. Разрешающий элемент равен 2 и находится на пересечении ведущего столбца и ведущей строки. Формируем новую симплекс-таблицу,
заменой X3 на X1:
Базис |
План |
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
|
|
|
|
|
X1 |
3 |
1 |
0 |
½ |
-1/2 |
0 |
|
|
|
|
|
|
|
X2 |
2 |
0 |
1 |
-1/6 |
½ |
0 |
|
|
|
|
|
|
|
X5 |
2 |
0 |
0 |
1/6 |
-1/2 |
1 |
|
|
|
|
|
|
|
L |
-12 |
0 |
0 |
-1/2 |
-1/2 |
0 |
|
|
|
|
|
|
|
Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи, где L(x) = -12.
Ответ при решении симплекс-методом совпадает с ответом при решении графическим методом, проверим решение с помощью Excel.
Результат на рисунке 2.
4
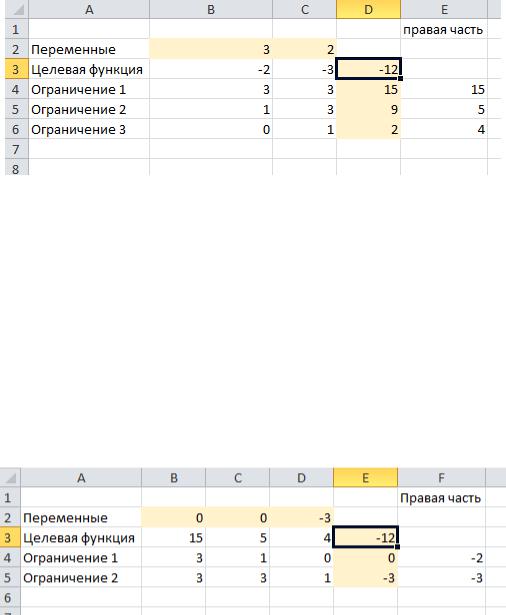
Рисунок 2 – Проверка в Excel
Далее была составлена задача, двойственная к заданной. Она выглядит следующим образом:
{
Полученная двойственная задача была проверена с помощью Excel. Это
представлено на рисунке 3.
Рисунок 3 – Проверка двойственной задачи
4.Вывод
Врезультате выполнения данной лабораторной работы были получены навыки решения задач линейного программирования графическим методом и симплекс-методом, а также поиска решение задачи с помощью MS Exсel.
В ходе работы проблем не возникло.
5
