lab3_graphs

1. Цель работы

Рассмотреть различные подходы к генерации случайных графов в ЭВМ. Провести анализ свойств созданных графов.

2. Ход работы

Вариант – 14. Выданные задания для реализации случайного графа и построения графиков представлены на рисунках 1-2 соответственно.

Рисунок 1 – Задание на реализацию случайного графа

Рисунок 2 – Задание на графики

Реализуется функция на построение случайного графа. Она принимает в качестве параметра вероятность p и размер задаваемого множества. В ней каждый элемент с определённой вероятностью присоединяется к подмножеству размером N. Если есть общие элементы между этими подмножествами, то между ними ставится ребро, листинг в Приложении.

Изображение графа с количеством вершин 20, вероятностью p=0.01 и M = N/2 представлено на рисунке 3, её спектр на рисунке 4.

Рисунок 3 – Изображение графа 1

Рисунок 4 – Спектр вершин графа 1

Изображение графа с количеством вершин 20, вероятностью p=0.01 и M = N представлено на рисунке 5, её спектр на рисунке 6.

Рисунок 5 – Изображение графа 2

Рисунок 6 – Спектр вершин графа 2

Изображение графа с количеством вершин 20, вероятностью p=0.01 и M = 2N представлено на рисунке 7, её спектр на рисунке 8.

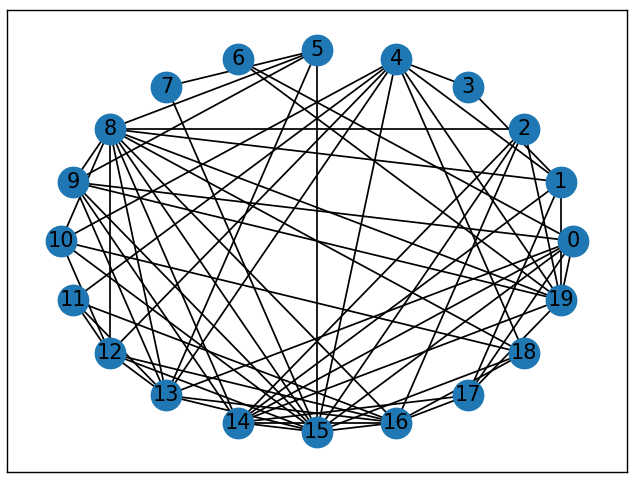
Рисунок 7 – Изображение графа 3

Рисунок 8 – Спектр вершин графа 3

При равных N=20 и p=0.01:

По первому спектру можно ожидать, что при размере подмножества M=N/2, степень вершин стремится к 1, либо вообще 0.

По второму спектру можно ожидать, что при размере подмножества M=N, степень вершин стремится к 4-5

По третьему спектру можно ожидать, что при размере подмножества M=2N, степень вершин стремится к среднему от 5 до 9

Теперь строятся графики зависимости среднего количества компонент связи в графе в зависимости p, заданного от 0.05 до 1 с шагом 0.05, при множествах M = N/2, N и 2N соответственно. Результат представлен на рисунке 9.

Рисунок 9 – Количество среднего компонент связи в графе от p

При меньшем размере множества следует, что меньше подмножеств пересекаются, соответственно выходит и меньше рёбер, где из-за большого количества вершин выходит при маленьком p выходит большое количество компонент связи. В подавляющем большинстве случаев вышло, что в графе всего один компонент связи при p > 0.15.

3. Вывод

В ходе лабораторной работы был построен случайный граф размером 100 вершин на основе выданного задания, построен спектр степеней его вершин. Была реализована функция для построения графиков зависимости количества компонент связи в графе в зависимости p. Данный граф мог бы использоваться в реальной жизни, например, для описания работы соц. сети, где вершины – это человек, а подмножества – это интересы. Если в этих подмножествах есть что-то общее, то между людьми строится «ребро.

Приложение

import numpy as np

from igraph import Graph, STRONG

import random

import matplotlib.pyplot as plt

import networkx as nx

def generate_graph(N, p, choice):

M = [[0 for i in range(N)] for j in range(N)]

subsets_list = [set() for _ in range(N)] # Список подмноженств

M_choice = {1: int(N/2 + 1), 2: N + 1, 3: N * 2 + 1}

elements = set(range(1, M_choice[choice]))

for i in range(N):

subset = set()

for element in elements:

if random.random() < p:

subset.add(element)

subsets_list[i] = subset

for i in range(N):

for j in range(i+1, N):

if subsets_list[i].intersection(subsets_list[j]):

n = len(subsets_list[i].intersection(subsets_list[j]))

M[i][j] = n

M[j][i] = n

return M

def draw_graph(matrix):

# Создаем объект графа на основе матрицы смежности

graph = nx.from_numpy_matrix(np.array(matrix))

weights = nx.get_edge_attributes(graph, "weight")

# Отрисовываем граф

pos = nx.circular_layout(graph)

nx.draw_networkx_nodes(graph, pos)

nx.draw_networkx_edges(graph, pos)

nx.draw_networkx_labels(graph, pos)

nx.draw_networkx_edge_labels(graph, pos, edge_labels=weights)

plt.show()

def degree(matrix):

n = len(matrix)

deg = [sum(matrix[i]) for i in range(n)]

plt.hist(deg)

plt.ylabel('Количество вершин')

plt.xlabel('Степень вершины')

plt.title('Спектр степеней графа')

plt.show()

def visualization():

ran = np.arange(0.05, 1, 0.05)

count_component = []

for p in ran:

c = []

for i in range(101):

matrix = generate_graph(100, p, 1)

g = Graph.Adjacency(matrix)

c.append(len(g.connected_components(mode=STRONG)))

count_component.append(np.mean(c))

plt.plot(ran, count_component, color='green', label='При M=N/2')

count_component = []

for p in ran:

c = []

for i in range(101):

matrix = generate_graph(100, p, 2)

g = Graph.Adjacency(matrix)

c.append(len(g.connected_components(mode=STRONG)))

count_component.append(np.mean(c))

plt.plot(ran, count_component, color='red', label='При M=N')

count_component = []

for p in ran:

c = []

for i in range(101):

matrix = generate_graph(100, p, 3)

g = Graph.Adjacency(matrix)

c.append(len(g.connected_components(mode=STRONG)))

count_component.append(np.mean(c))

plt.plot(ran, count_component, label='При M=2N')

plt.xlabel('Вероятность p')

plt.ylabel('Количество компонент связи')

plt.title('Количество компонент связи в зависимости от M')

plt.legend()

plt.show()

def main():

m = generate_graph(20, 0.1, 1)

draw_graph(m)

degree(m)

m = generate_graph(20, 0.1, 2)

draw_graph(m)

degree(m)

m = generate_graph(20, 0.1, 3)

draw_graph(m)

degree(m)

# Задание 4

visualization()

main()