lab2_graphs

1.Цель работы

Реализовать и проверить на тестовом примере базовый алгоритм на графе. Сравнить быстродействие реализованного алгоритма на специальных графах.

2.Ход работы

Создаѐтся неориентированный граф без весов для тестирования базового алгоритма. Его представление в матрице смежности и изображение на рисунках 1-2 соответственно.

Рисунок 1 – Матрица смежности графа

Рисунок 2 – Изображение графа Реализуется выданный по варианту алгоритм – алгоритм поиска

кратчайшего маршрута (поиск в ширину). Его блок-схема представлена на рисунке 3.

2

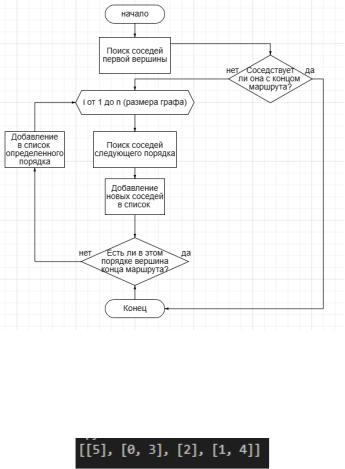
Рисунок 3 – Блок-схема алгоритма Созданный алгоритм применяется на указанном выше графе. Результат

представлен на рисунке 4.

Рисунок 4 – Результат работы алгоритма Алгоритм искал кратчайший путь от точки 0 до точки 4. Алгоритм

ищет соседей точки, добавляет их в n-й список, который является порядком.

Далее в следующем порядке ищутся соседи соседей и так далее. Описание переменных функции представлен в таблице 1, листинг в Приложении.

Таблица 1 – Описание переменных функции breadeth_shortest_way

Реализуется создание графа с правильной треугольной решѐткой.

Изображение графа 3 x 3 представлено на рисунке 5, листинг создания в Приложении.

Рисунок 5 – Граф с правильной треугольной решѐткой

Графы такого типа M x M тестируются на созданном алгоритме несколько раз с количеством узлов от 4 до 81. Результат быстродействия работы алгоритма в зависимости от вершин представлен на рисунке 6.

Рисунок 6 – График зависимости t от M в алгоритме

4

3.Дополнительное задание

Также в рамках дополнительного задания создается функция dop_task,

которая по матрице смежностей выдаѐт узлы графов, между которым максимальная длина пути. Переменные, используемые в функции,

представлены в таблице 2. Листинг функции представлен в Приложении.

Таблица 2 – Переменные функции dop_task

Функция с переданным параметром df вывела список с одним из

маршрутов [0, 1, 4], где 4 – действительно максимальная длина маршрута в

графе.

4.Вывод

Впрактической ходе работы был реализован алгоритм поиска кратчайшего пути в графе (поиск в ширину). Этот алгоритм был протестирован на простом графе. С помощью специальных графов с правильной треугольной решѐткой была протестирована работа этого алгоритма в зависимости от количества вершин. Судя по полученному графику, можно сделать вывод, что с каждым увеличением количества вершин M время работы алгоритма увеличивается линейно. В реальной практике такой алгоритм мог бы рассчитывать расстояние между городами.

Входе работы проблем не возникло.

5

Приложение

import pandas as pd import numpy as np

import matplotlib.pyplot as plt import networkx as nx

import time

matrix = [[0, 1, 1, 0, 0, 1], [1, 0, 1, 0, 0, 0], [1, 1, 0, 1, 1, 0], [0, 0, 1, 0, 0, 1], [0, 0, 1, 0, 0, 0], [1, 0, 0, 1, 0, 0]]

matrix2 = [[0, 0, 0, 0, 0, 1], [0, 0, 1, 0, 0, 0], [0, 1, 0, 1, 1, 0], [0, 0, 1, 0, 0, 1], [0, 0, 1, 0, 0, 0], [1, 0, 0, 1, 0, 0]]

def get_list_edges(df):

"""Построение списка рёбер"""

edges_list = []

for i in range(len(df.values)):

for j in range(len(df.values[i])): if df.values[i][j] != 0:

edges_list.append([i, j, df.values[i][j]]) return edges_list

def visualisation_graph(edges_list, length):

"""Визуализация графа"""

graph = nx.DiGraph() graph.add_nodes_from(length) graph.add_weighted_edges_from(edges_list) pos = nx.spring_layout(graph) nx.draw(graph, node_size=2000, pos=pos,

with_labels=True)

edge_labels = nx.get_edge_attributes(graph, "weight") nx.draw_networkx_edge_labels(graph, pos, edge_labels=edge_labels) plt.show()

def find_neighbours_matrix(graph_index, df):

"""Поиск соседей по матрице"""

neighbours_list = []

for j in range(len(df.values[graph_index])): if df.values[graph_index][j] != 0:

neighbours_list.append(j)

6

return neighbours_list

def breadeth_shortest_way(df, vertexes):

"Алгоритм поиска кратчайшего пути в ширину" neighbours = []

neighbours.append(find_neighbours_matrix(vertexes[0], df)) if vertexes[1] in neighbours[0]:

return len(neighbours) count = 0

while count < len(df): temp = []

for vertex in neighbours[count]: temp.extend(find_neighbours_matrix(vertex, df))

if vertexes[0] in temp: temp.remove(vertexes[0])

for i in temp:

for j in range(len(neighbours)): if i in neighbours[j]: temp.remove(i)

break neighbours.append(list(set(temp))) if vertexes[1] in neighbours[-1]:

break count += 1

return len(neighbours)

def regular_triangular_lattice(M):

"Построение графа с правильной треугольной решёткой" matrix = np.zeros((M**2, M**2))

for V in range(len(matrix)-1): R = V // M # номер строки

C = V % M # номер столбца if C < M:

matrix[V][V+1] = matrix[V+1][V] = 1 if R < M**2 and (V < M**2 - M):

matrix[V][V+M] = matrix[V+M][V] = 1

if (R % 2 == 0 and C % 2 == 0) or (R % 2 == 1 and C % 2 == 1): if C > 0:

matrix[V][V+M-1] = matrix[V+M-1][V] = 1 if C < M:

matrix[V][V+M+1] = matrix[V+M+1][V] = 1

# Удаление лишних ребер i = M - 1

j = M

for k in range(M - 1): try:

matrix[i][j] = 0 matrix[j][i] = 0 matrix[i][j+M] = 0 matrix[j+M][i] = 0

except BaseException:

7

pass i += M j += M

return matrix

def dop_task(df): temp = []

for i in range(len(df)):

for j in range(i, len(df)): if i != j:

temp.append([i, j, breadeth_shortest_way(df, [i, j])]) t = [0, 0, 0]

for i in range(len(temp)): if temp[i][2] > t[2]:

t = temp[i]

return t

def main():

# Задание 1 m = matrix2 length = []

[length.append(i) for i in range(len(m))]

df = pd.DataFrame(np.array(m), columns=length, index=length)

visualisation_graph(get_list_edges(df), length)

# Задание 2 и 3 print(breadeth_shortest_way(df, [0, 4]))

# Доп задание print(dop_task(df))

# Задание 4

m = regular_triangular_lattice(3) length = []

[length.append(i) for i in range(len(m))]

df = pd.DataFrame(np.array(m), columns=length, index=length)

visualisation_graph(get_list_edges(df), length)

# Задание 5

N = list(np.arange(2, 10)) t = []

for n in N:

m = regular_triangular_lattice(n) length = []

[length.append(i) for i in range(len(m))]

df = pd.DataFrame(np.array(m), columns=length, index=length)

start = time.time() for i in range(10):

breadeth_shortest_way(df, [0, len(df)]) t.append((time.time() - start)/10)

N = [num**2 for num in N]

8

plt.plot(N, t)

plt.xlabel('Количество узлов в графе') plt.ylabel('Время быстродействия t') plt.title('График зависимости t от M в алгоритме') plt.show()

main()

9