
4016_Жовтяк_ЛР_3_вер_1
.docxГУАП
КАФЕДРА № 41
ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
ассистент |
|
|
|
Н.В. Апанасенко |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3 |
АНАЛИЗ РАБОТЫ ЭЛЕМЕНТАРНОЙ СИСТЕМЫ МНОЖЕСТВЕННОГО ДОСТУПА НА ОСНОВЕ АППАРАТА МАРКОВСКИХ ПРОЦЕССОВ |
по курсу: ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ, СЕТИ И ТЕЛЕКОММУНИКАЦИИ |
|
|
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
4016 |
|
|
|
М. О. Жовтяк |
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург 2022
Цель работы:
Анализ работы элементарной системы множественного доступа. Оценка среднего количества абонентов, находящихся в системе.
Теоретические сведения:
Для анализа элементарной системы множественного доступа воспользуемся аппаратом Марковских процессов с дискретным временем и состоянием. Опишем количество абонентов, имеющих сообщения для передачи Марковской цепью переходных состояний. Каждое состояние обозначает количество активных абонентов в системе. Марковская цепь показана на рисунке 1.

Рисунок 1 – Марковская цепь для модели случайного множественного доступа
Опишем вероятности переходов из одного состояния в другое:
Вероятность перехода из состояния «ноль» в произвольное состояние j.
Переход
из состояния 0 в состояние j
может произойти, только когда количество
АБ, у которых появилось сообщение будет
равно j,
то есть
 .
Так как
.
Так как
 распределено по закону Пуассона получаем:
распределено по закону Пуассона получаем:
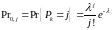
Вероятность перехода из i-го состояния в i-1.
Событие
перехода из состояния i
в состояние i-1
означает, что новых АБ не появилось, и
один АБ передал сообщение. То есть
 и
и
 :
:

Вероятность «успеха» (один АБ передавал, остальные не передавали), определяется как:

Вероятность отсутствия новых АБ определяется как:

Вероятность остаться в состоянии i.
Переход из состояния i в i. может произойти в случае, если один АБ передал сообщение, и один новый АБ появился, или если новых АБ не было, и ни один не передал:

Вероятность того, что ни один АБ не передал сообщение определяется как:

Вероятность перехода из состояния i в состояние j.
Переход из состояния i в j может произойти в случае, если один АБ передал сообщение и появились (j-i+1) АБ-ов, или если ни один не передал сообщение и появились (j-i) АБ-ов. Вероятность данного события определяется как:

Если
вероятность передачи активными АБ - p
является константой, то есть не зависит
ни от количества активных АБ в текущем
слоте, ни от интенсивности появления
активных АБ, то такая система является
неустойчивой (количество абонентов, у
которых имеется сообщения для передачи
неограниченно возрастает при
 ).
).
Используя
описанные выше вероятности переходов
из одного состояния в другое, можно
сформировать систему усеченных линейных
уравнений, для фиксированного значения
 :
:


Решая
данную систему усеченных линейных
алгебраических уравнений (количество
уравнений K),
для фиксированного
,
получим вектор стационарного распределения,
каждое из значений
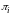 означает вероятность того, что в системе
находится i
абонентов.
означает вероятность того, что в системе
находится i
абонентов.
Тогда оценить среднее количество абонентов, находящихся в системе множественного доступа можно как:
 ,
,
где
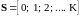 .
.
Задание:
Нахождение среднего количества пользователей в системе методом решений систем линейных уравнений и методом моделирования, разработанного в лабораторной работе №1, представлено в Приложении. Так было построено несколько графиков в зависимости от λ при размерности матрицы переходов K = [10, 50, 100, 170]. Они представлены на рисунках 2-

Рисунок 2 – График при K = 10
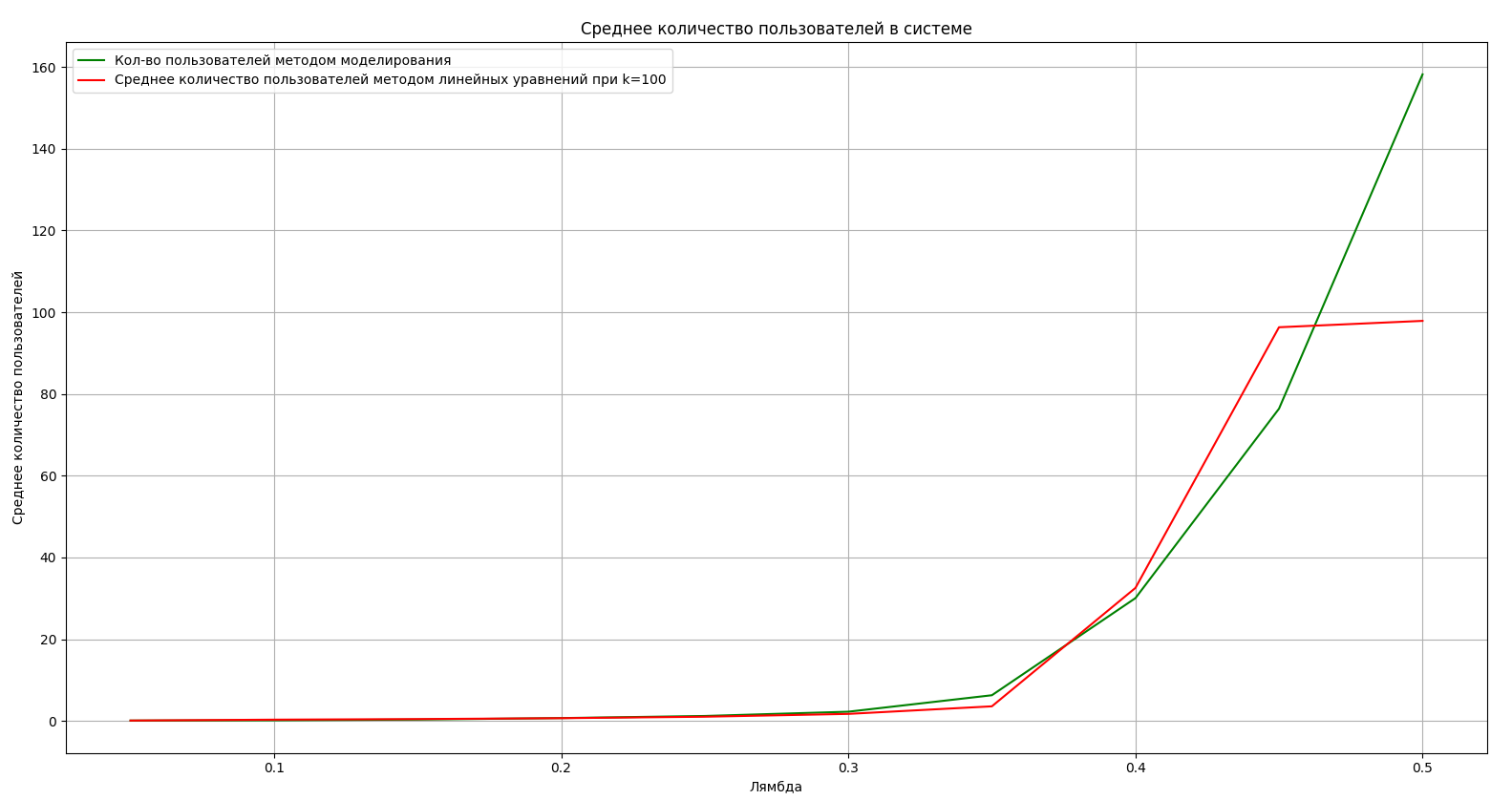
Рисунок 3 – График при K = 50
Рисунок 4 – График при K = 100

Рисунок 5 – График при K = 170
Из графика видно, что до значения 0.35 графики почти не отличаются, их отличия могут быть связаны с особенностями работы с большими числами и числами с плавающей точкой в python для метода решения системы линейных уравнений. Отличия графиков после 0.35, когда система становится не работоспособной, заключается в том, что при методе решением системы линейных уравнений среднее значение определяется как максимально возможно достижимое при учете количества линейных уравнений, а методом моделирования, количеством пользователей, которые не успели выйти из системы за определенное количество шагов. Так как графики близки к друг другу, можно сделать вывод, метод моделирования и метод решения системы линейных уравнений дает нам одинаковый прогноз результата работы системы. При значении λ меньше 0.35, система находится в работоспособном состоянии. При большем значении система не справляется с обслуживанием абонентов.
Код программы представлен в приложении А.
Дополнительное задание:
Рассматривается беспроводная система передачи данных, состоящая из одной базовой станции (БС) и абонентов (АБ) равномерно распределенных вокруг базовой станции БС.
В этой модели пропускная способность канала связи С между БС и АБ равна:
![]()
В модели используется модель затухания сигнала по Окамура-Хата:

В данной модели рассматривается алгоритм распределения ресурсов Equal blind.
Данный алгоритм обеспечивает равные скорости между всеми абонентами. Доля ресурса времени, выделяемая каждому абоненту (выравнивает скорость):

Скорость для абонента i может быть выражена как:

Теперь с заданным количеством пользователей (64) анализируется зависимость скорости Di от количества пользователей, взаимодействующих с БС. Результат представлен на рисунке 6.

Рисунок 6 – График зависимости средней скорости от количества пользователей
Проанализировав график можно сделать следующий вывод. На начальном этапе, когда мало пользователей сети, скорость очень высокая, но далее скорость многократно уменьшается и стремится к почти нулевой. Это связано с сутью самой модели Equal Blind, где в независимости от того, на каком расстоянии АБ находится от БС, пользователь получит одинаковую скорость, а ресурсы БС не бесконечны. Если бы все пользователи находились на одинаковом расстоянии от БС, тогда бы скорость равномерно одинаково зависела от количества АБ подобно линейной функции. В неидеальной модели расстояние абсолютно случайно, поэтому скорость так быстро уменьшается на начальном этапе.
Код программы представлен в приложении Б.
Вывод:
В результате выполнения лабораторной работы было определено среднее количество абонентов в системе методом решения системы линейных уравнений и произведено сравнение с результатами, полученными методом моделирования. На основе этого был сделан вывод о неработоспособности системы.
Приложение А
import math
import numpy as np
import matplotlib.pyplot as plt
import copy
# (C(1, i)*p(1-p)**(i-1))
def c_p(i):
if i == 0:
return 0
else:
return (1-1/i)**(i-1)
# Вероятность перехода из состояния ноль в произвольное j
def zero_to_j(lymbda, j):
Pr = ((lymbda**j)*(math.e**(-1*lymbda)))/(math.factorial(j))
return Pr
# Верояность перехода из i в i-1
def i_stepback(lymbda, i):
P = math.e**(-lymbda)
return c_p(i) * P * 0.4
# Вероятность остаться в i
def i_stay(lymbda, i):
a = (1 - i_stepback(lymbda, i))*math.e**(-lymbda)
b = (i_stepback(lymbda, i))*lymbda*(math.e**(-lymbda))
return (a+b)
# Вероятность перехода из состояния i в состояние j
def i_to_j(lymbda, i, j):
a = i_stepback(lymbda, i)*((lymbda**(j-i+1))*(math.e**(-lymbda))/math.factorial(j-i+1))
b = (1-i_stepback(lymbda, i))*((lymbda**(j-i))*(math.e**(-lymbda))/math.factorial(j-i))
return (a+b)
# Создание матрицы
def random_matrice(lymbda, size):
matrice = []
row, column = size, size
for i in range(row):
new_row = []
for j in range(column):
if j == i:
p = i_stay(lymbda, j)
elif j == 0:
p = zero_to_j(lymbda, i)
elif j < i:
p = i_to_j(lymbda, j, i)
elif j - 1 == i:
p = i_stepback(lymbda, j)
else:
p = 0
new_row.append(p)
matrice.append(new_row)
for i in range(len(matrice)):
row_sum = sum(matrice[i])
matrice[i] = [j/row_sum for j in matrice[i]]
return matrice
# Решение системы линейных уравнений из лабы 2
def system(P, size):
P = np.array(P)
P = np.transpose(P)
# система уравнений после равно
P_y = []
# до равно
P_x = copy.deepcopy(P)
for i in range(size):
if i == len(P) - 1:
P_x[i] = [1]*size
P_y.append(1)
else:
for j in range(size):
if i == j:
P_x[i,j] -= 1
P_y.append(0)
pi = np.linalg.solve(P_x,P_y)
S = []
for i in range(size):
S.append(i)
abonents = pi.dot(S)
#print(np.mean(abonents))
#print('Стационарное распределение: ', pi)
return np.mean(abonents)
# Построние графика
def main(lymbda_spisok, k):
abonents = []
for lymbda in lymbda_spisok:
abonents.append(system(random_matrice(lymbda, k), k))
#print(abonents)
#print(lymbda_spisok)
plt.plot(lymbda_spisok, list(reversed(abonents)), color='r', label=f'Среднее количество пользователей методом линейных уравнений при k={k}')
plt.xlabel('Лямбда')
plt.ylabel('Среднее количество пользователей')
plt.legend()
plt.grid()
title = 'Среднее количество пользователей в системе'
plt.title(title)
plt.show()
def lab1():
# Кол-во слотов в сети
slot = 1000
# Список значений лямбды
lambdaa = np.arange(0.05, 0.51, 0.05)
# Кол-во пользователей в слоте
Nk = 0
# Суммарные значения кол-ва пользователей в каждом слоте
summ_abonents = 0
# Список для среднего кол-ва абонентов
n = []
# Список для среднего количества слотов, для передачи сообщения одним абонентом
t = []
# Итерация лямбды
for lamb in lambdaa:
# распределение пользователей на слоты по пуасноу
puason = np.random.poisson(lamb,slot)
# Итерация слотов
for i in range(slot):
# Первая передача сообщений
if i == 0:
Nk = puason[0]
summ_abonents += Nk
# Передача сообщений
else:
try:
# Количество пользователей, собирающихся передать сообщение в слоте
binomial = np.random.binomial(n= Nk, p=1 / Nk)
except:
# Никто не передает сообщения
binomial = 0
if binomial == 1:
# Один пользователь передает сообщение
Nk = Nk + puason[i] - 1
summ_abonents += Nk
else:
# Передача сообщений, не равным 1
Nk = Nk + puason[i]
summ_abonents += Nk
# Сохраняем N и T
n.append((1/slot)*summ_abonents)
t.append(n[-1]/lamb)
# Проверка среднего количества слотов для передачи сообщений одним пользователем
#Создание графиков
plt.plot(lambdaa, n,color = "g", label='Кол-во пользователей методом моделирования')
# Показываем графики
# Список значений лямбды
lymbda_spisok = np.arange(0.05, 0.51, 0.05)
# K задает пользователь
k = 170
#system(random_matrice(0.05, 3), 3)
lab1()
main(lymbda_spisok, k)
Приложение Б
import math
import numpy as np
from numpy import log10
import matplotlib.pyplot as plt
import random
# Константа частоты сигнала
f = 868
df = 50 * 10**6
# Константа высот антенн базовых станций
h = 10
# Константа высоты антенны мобильной станции
height = 1.5
# Вычисление пропускной способности C по формулам
def traffic(distance):
traffic = []
a = (1.1*log10(f)-0.7)*height-(1.56*log10(f)-0.8)
for i in distance:
ldb = 46.3+33.9*log10(f)-13.82*log10(10)-a+(44.9-6.55*log10(height))*log10(i)
l = 10**(ldb/10)
c = df * np.log2(1+(1.5/(l*df*300*3*1.38*10**(-23))))
traffic.append(c)
return traffic
# Расчет скорости D
def speed(C):
C_1 = []
for i in range(len(C)):
C_1.append(1/C[i])
D = (1/(sum(C_1)))
return D
users = list(range(1, 64))
D = []
for i in range(1, users[-1]+1):
D_mean = []
for j in range(1, 1000):
distances = []
for k in range(i):
distances.append(random.uniform(0, 5.5))
D_mean.append(round(speed(traffic(distances)))/10**6)
D.append(np.mean(D_mean))
plt.plot(users, D)
plt.title('График зависимости средней скорости Dmean от количества пользователей N')
plt.xlabel('Количество АБ')
plt.ylabel('Пропускная способность Мбит/c')
plt.show()
