4016_Жовтяк_ЛР_2_вер_1

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ассистент				Н.В. Апанасенко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

АНАЛИЗ МАРКОВСКОЙ ЦЕПИ С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ

по курсу: ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ, СЕТИ И ТЕЛЕКОММУНИКАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2022

1. Цель работы

Получение навыков моделирования алгоритмов случайного множественного доступа в системах передачи данных.

2. Краткие теоретические сведения

Марковская цепь является частным случаем конечного автомата, вероятностные характеристики перехода которого в какое-либо состояние зависит только от текущего. Если переходы между состояниями возможны только в фиксированные моменты времени, то говорят, что такие цепи работают в дискретном времени. Важным классом Марковских цепей являются однородные цепи, структура которых представима в виде матрицы переходных вероятностей P.

Элемент матрицы p_i,j соответствует вероятности перехода из i-го состояния в j-ое за один шаг. Подобные цепи так же удобно представить в виде ориентированного графа со следующей структурой. Узлами графа являются все возможные состояния S₁, S_2,…, S_n системы S, а ребрами - переходы из состояния в состояние с весам, соответствующими переходным вероятностям. Пример такого графа для цепи, содержащей четыре возможных состояния, представлен на рисунке 1.

Случайный процесс, порожденный такой системой, представляет собой последовательность принимаемых ею состояний.

Рис. 1. Граф состояний для системы S.

Обозначим через - вектор вероятностей, соответствующий начальному состоянию системы. Зная вероятности переходов и начальные вероятности можно вычислить вероятности нахождения случайного процесса на шаге i в том или ином состоянии, обозначаемые вектором . Для однородной Марковской цепи

В общем случае:

Для однородной Марковской цепи можно определить вероятность перехода из состояния S_i в состояние S_j за m шагов:

Данное равенство означает, что для попадания в состояние S_j из состояния S_i за m необходимо сначала попасть в состояние S_k за (m-1) шагов, а затем за один шаг перейти из S_k в S_j. Цепь Маркова называется неприводимой, если каждое ее состояние может быть достигнуто из любого другого, то есть существует целое число m₀ (которое может зависеть от i и j) такое, что .

Обозначим вероятность возврата в состояние S_j через m шагов после ухода из этого состояния как . Состояние называется возвратным, если вероятность попадания в него за конечное число шагов равна единице: . В другом случае состояние относится к невозвратным.

Очевидно, что среднее число шагов для возврата в это же состояние определяется как:

Состояние называется возвратным нулевым, если среднее время возвращения в него равно бесконечности, и возвратным ненулевым, если это время конечно.

Если единственными возможными шагами, на которых система может вернуться в состояние S_j, являются шаги ɣ, 2 ɣ, 3 ɣ, … , (где ɣ>1 и являются наименьшим целым числом, обладающим таким свойством), то состояние S_j называется периодическим с периодом ɣ, если ɣ = 1, то S_j называют апериодическим.

Состояние S_j называется эргодическим, если оно является апериодическим, возвратным и ненулевым. Если все состояния цепи Маркова эргодичны то, сама цепь Маркова называется эргодической.

Если Марковская цепь является эргодической, однородной неприводимой и апериодической то существуют предельные вероятности состояний (стационарное распределение), и они не зависят от начального состояния системы:

Интерпретировать данное выражение можно следующим образом. Обозначим через N_j­ количество раз, когда система S находится в состоянии S_j, а общее количество совершенных шагов N, тогда оценить стационарное распределение можно как:

Стационарное распределение можно найти, решая систему линейных алгебраических уравнений (СЛАУ) совместно с так называемым условием нормировки которая имеет следующий вид:

После умножения вектора на матрицу переходных вероятностей P получим следующую систему уравнений:

Данная система является переопределенной. Но так как нормировочное условие дает возможность вычислить все предельные вероятности, систему можно записать в следующем виде, исключив одно уравнение:

Решением данной системы уравнений является искомое стационарное распределения.

3. Результат и описание программы

В программе согласно варианту формируется матрица переходных вероятностей с использованием псевдослучайных чисел random(‘seed’, 132*15), где 15 мой номер в списке. Матрица представлена на рисунке 2.

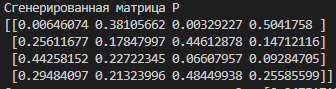
Рисунок 2 – Сформированная матрица переходных состояний

В результате решения системы линейных алгебраических уравнений был получен список, содержащий стационарные распределения π₁- π₄. Результат представлен на рисунке 3.

Рисунок 3 – Результат решения СЛАУ

При различных значениях начального распределения вероятностей и различных значения t, которое задано в качестве 10, получены стационарные распределения, представленные на рисунке 4.

Рисунок 4 – Стационарные распределения при различных начальных вероятностях

График зависимости оценки стационарного распределения от t представлен на рисунке 5.

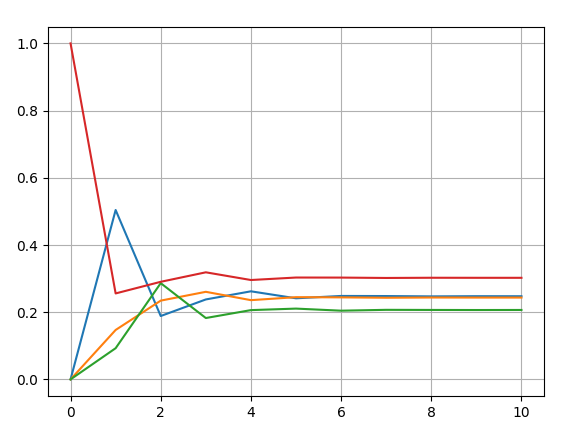
Рисунок 5 - График зависимости оценки стационарного распределения от t

Аналогично значения стационарного распределения Марковского случайного процесса методом имитационного моделирования при различных начальных состояниях представлено на рисунке 6.

Рисунок 6 - Стационарные распределения Марковского случайного процесса

Одним из примеров порожденного цепью случайного процесса является прогноз погоды. Задано 4 состояния погоды: ясно, пасмурно, дождь, туман. Из каждого состояния с вероятностью p_i, заданной в матрице, можно перейти в другое состояние, то есть предсказать погоду. И так далее каждый шаг. Количество дней каждого состояния за определенное количество дней (1000) представлено на рисунке 7.

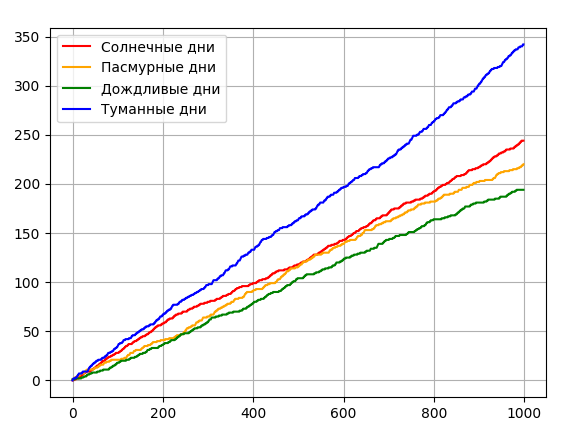
Рисунок 7 – Типы погод каждого дня за 1000 дней

Переходы примерно одинаковы. Если разделить количество дней каждого состояния на количество дней, то получится список стационарных распределений.

Сравнив значения стационарных распределений, полученного тремя способами, можно увидеть, что они абсолютно одинаковы. Это значит, что решение представлено верное.

В таблице 1 представлен список используемых переменных.

Таблица 1

Список используемых переменных

Название	Тип	Описание
Size	Int	Размер матрицы
Row_sum	Float	Сумма строки
P	List	Матрица переходных вероятностей
P_y	List	СЛАУ (после равно)
P_x	List	CЛАУ (до равно)
Pi	List	Список стационарного распределения первого пункта
Vector_pi	List	Начальный вектор вероятностей
Graph	List	Список, хранящий значения для построения графиков
Steps	List	Количество дней для примера Марковского процесса
Positions	List	Список хранения позиций переходов
Start_position	int	Переходная переменная для хранения стартовой позиции для перехода
Results	Dictionary	Словарь для хранения всех переходов
Sun, cloud, rain, fog	List	Списки для отображения графика переходов примера Марковского процесса

На рисунке 8 представлена блок схема программы. В приложении представлен листинг.

Рисунок 8 – Блок-схема разработанной программы

4. Вывод

В ходе лабораторной работы были подсчитаны стационарные распределения матрицы переходных вероятностей путем трех способов: решением СЛАУ, при различных значениях начального распределений в зависимости от t и путем имитации Марковского процесса. В каждом случае стационарное распределение выходило одинаковым, что означает о правильности реализации данных методов. Также по построенным графикам был сделан вывод о том, что вне зависимости от начального состояния, через некоторое количество шагов вероятности все равно придут к стационарному распределению.

Приложение

import random

import numpy as np

import matplotlib.pyplot as plt

import copy

# Функция генерации псевдослучайного числа согласно варианту 15

random.seed(132*15)

size = 4

# Генерация матрицы переходных вероятностей

P = [[random.random() for j in range(size)] for i in range(size)]

for i in range(len(P)):

row_sum = sum(P[i])

P[i] = [j/row_sum for j in P[i]]

P = np.array(P)

P = np.transpose(P)

print('Сгенерированная матрица P')

print(P)

# решение системы линейных уравнений относительно вектора пи

def task2(P):

# система уравнений после равно

P_y = []

# до равно

P_x = copy.deepcopy(P)

for i in range(size):

if i == len(P) - 1:

P_x[i] = [1]*size

P_y.append(1)

else:

for j in range(size):

if i == j:

P_x[i,j] -= 1

P_y.append(0)

pi = np.linalg.solve(P_x,P_y)

print('Стационарное распределение пункт 2: ', pi)

# стационарное распределение при различных начальных вероятностей

def task3(P):

vector_pi = [0, 0, 0, 1]

graph = []

graph.append(vector_pi)

fig, ax = plt.subplots()

# умножение матрицы на вектор

for i in range(10):

vector_pi = np.dot(P,vector_pi)

graph.append(vector_pi)

print('Стационарное распределение пункт 3: ', vector_pi)

plt.plot(graph)

plt.grid()

plt.show()

# стационарное распределение при имитационном моделировании

def task4(P):

P = np.transpose(P)

steps = 1000

positions = np.arange(0,size)

start_position = np.random.randint(0,size)

results = dict.fromkeys(positions, 0)

results[start_position] += 1

graph = []

for i in range(steps):

start_position = random.choices(positions, weights = P[start_position])[0]

results[start_position] += 1

graph.append(list(results.values()))

for i in results.keys():

results[i] = results[i]/steps

print('Стационарное распределение пункт 4: ', list(results.values()))

sun, cloud, rain, fog = [], [], [], []

for i in range(len(graph)-1):

sun.append(graph[i][0])

cloud.append(graph[i][1])

rain.append(graph[i][2])

fog.append(graph[i][3])

plt.plot(sun, label='Солнечные дни', color='red')

plt.plot(cloud, label='Пасмурные дни', color='orange')

plt.plot(rain, label='Дождливые дни', color='green')

plt.plot(fog, label='Туманные дни', color='blue')

plt.legend()

plt.grid()

plt.show()

task2(P)

task3(P)

task4(P)