ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ассистент				Н.В. Апанасенко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

АНАЛИЗ ЭЛЕМЕНТАРНОЙ СИСТЕМЫ МНОЖЕСТВЕННОГО ДОСТУПА

по курсу: ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ, СЕТИ И ТЕЛЕКОММУНИКАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016				М.О. Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2022

1. Цель работы

Получение навыков моделирования алгоритмов случайного множественного доступа в системах передачи данных.

2. Краткие теоретические сведения

Задача лабораторной работы заключается в моделировании работы сети, где каждый промежуток времени может прийти случайное количество пользователей, как и случайно определяется количество пользователей, которые передают сообщения. Ситуации такие:

1. Событие «успех». Если в слоте с индексом k передает только один абонент, считается, что сообщение доставлено успешно. Абонент, успешно передавший сообщение, покидает систему.

2. Событие «конфликт». Если в слоте k передают два и более абонентов, то в этом случае считается, что сообщение не доставлено – произошел конфликт. Абоненты остаются в системе и осуществляют попытки передачи сообщения в следующих слотах.

3. Событие «пусто». В слоте не передает ни один из абонентов.

Количество пользователей на слоте:

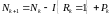, где N_k – количество пользователей на слоте k, P_k – количество пользователей , подключившихся к сети, в данном слоте, I {R_k = 1} – числовая функция, принимающая значение 1, если R_k = 1, в остальных случаях принимает значение 0, R_k - количество пользователей, передающий сообщение в одном слоте.

При этом, P_k и R_k определяются случайным образом:

1. R_k = С_S^k * p^k*q^S-k c вероятностью передачи каждым абонентом в слоте k,

2. P_k - находится по закону Пуассона с параметром (P_k = λ^k*e^-λ/k!), принадлежащего к диапазону [0,05; 0,5] с шагом 0,05.

Для данной сети строится цепь Маркова, показанная на рисунке 1

Рисунок 1 – Цепь Маркова

Из цепи Маркова видно, что прямые переходы(вправо) можно производить в любое состояние, в обратную(влево) же сторону только на одно состояние.

Вероятности переходов из одного состояния в другое показаны ниже. В общем случае вероятность высчитывается так: P_0,j = λ^j * e^-λ/ j!

Для переходи из 0 в 0 - P_0,0 = e^-λ

Для переходи из i в j – P_i,j = P_r{R_k = 1 }* P_r{P_k = j-i+1} + P_r{R_k != 1 }* P_r{P_k = j-i}

Для переходи из i в j-1 - P_i,j-1 = P_r{R_k = 1 }* P_r{P_k = 0}

Для переходи из i в i- P_i,j = P_r{R_k != 1 }* P_r{P_k = 0} + P_r{R_k = 1 }* P_r{P_k = 1}

3. Описание программы

Обходятся все значения лямбды с шагом 0,05, для каждой лямбды получаем количество пользователей, распределённое по закону Пуассона, далее для каждого слота находим количество пользователей, в первом слоте количество пользователей равно первому значению из распределения Пуассона, для остальных слотов , с помощью биномиального распределения, находится количество пользователей, передающих сообщение, вероятность передачи сообщения одним пользователем – 1/N_k , если N_k ноль, то количество пользователей, передающих сообщение тоже ноль, далее, основываясь на количестве пользователей, передающих сообщение вычисляется количество пользователей на слоте. Если сообщение передаёт 1 пользователь, то количество пользователей определяется как N_k+1 = N_k + P_k – I {R_k = 1}, в остальных случаях как N_k+1 = N_k + P_k. Для каждой лямбды вычисляется сумма пользователей на каждом слоте и делится на количество слотов (S), тем самым получается среднее количество абонентов в системе (N = ), далее среднее количество абонентов делится на лямбда, и получается среднее количество слотов необходимое для передачи сообщения одним абонентом (T = N/λ). По полученным значениям N и T строится графики N от λ, T от λ.

Результат вывода графиков представлен на рисунке 2.

Рисунок 2 – Графики зависимости N и T от λ

Из рисунка 2 можно увидеть, что рост среднего количества абонентов начинает резко увеличиваться c λ = 0,35. Это показывает, что количество пользователей приходящих становится слишком много, для обработки всех запросов, из-за чего растёт и время нахождения пользователей в системе, причём время нахождения растёт сильнее, чем количество пользователей, что говорит о неспособности данной системы работать с большим количеством пользователей.

Если приблизить график к точке расхода линий (что видно на рисунке 3), то можно увидеть, что до λ = 0,35, T и N равны неизменно 22 и 7 соответственно. Это значит, что оптимальное среднее количество элементов в системе равно 7. Больше этого система становится перегруженной.

Рисунок 3 – Увеличенный масштаб графика