ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., канд. техн. наук				А. В. Аграновский
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №6

РАБОТА С МАССИВАМИ

по курсу: ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016				Жовтяк М.О.
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2022

Вариант 15 (15 задание)

Постановка задачи

Дано целое число N. Без использования сторонних библиотек сгенерируйте магический квадрат размером N*N.

Входные данные: целое число N.

Выходные данные: двумерный массив magic.

Сторонние библиотеки не должны использоваться.

Дополнительные требования к программе не были выявлены.

Математическая модель

Для построения магического квадрата будет применен метод Де ла Лубера. Сначала верхнее центральное место квадрата заполняется цифрой 1. Далее, начиная с этого места происходит последовательное движение для заполнения квадрата по диагонали вверх и вправо. Если диагональ покидает квадрат, то он переносится в последний или первый столбец соответственно.

В данном случае такой способ применим для квадратов типа 3x3, 5x5 и т.д. Поэтому число N должно быть нечетным.

Описание разработанной программы

Первым делом, программа принимает входную переменную N для основной функции. Она проверяется на соответствие условию, что она целая и нечетная. Далее выполняется основная функция: сначала создается двумерный массив, внутри которого N массивов с N количеством пустых элементов. После этого центральный элемент 0 массива заполняется единицей. И далее выполняется цикл, суть которого описана в математической модели.

Таблица 1 демонстрирует список используемых переменных.

Таблица 1 - Описание переменных

Имя переменной	Тип переменной	Назначение переменной
N	int	Параметр основной функции, размер магического квадрата
n	int	Промежуточная переменная для генерации N
num	int	Промежуточный размер, используемый для заполнения matrix
magic	list	Итоговый двумерный массив, хранящий в себе магический квадрат
matrix	list	Промежуточный массив для записи магического квадрата
x	int	Номер столбца для вхождения элемента в matrix
y	int	Номер строки для вхождения элемента в matrix
Old_x	int	Запись номера столбца для вхождения элемента в matrix
Old_y	int	Запись номера строки для вхождения элемента в matrix

Описание алгоритма работы программы представлено в виде блок схемы на рисунке 1.

Рисунок 1 – Блок-схема алгоритма

Вычислительная сложность реализованного алгоритма в нотации O() является линейной (O(n)).

Код программы:

# ввод N

def getting_n():

while True:

try:

n = int(input("Введите размер магического квадрата: "))

return n

except:

print("Ошибка. N - целое число")

# основная функция

def LAB6_VAR15(num):

try:

# проверка входных данных

if num % 2 == 0 and not num.isdigit():

return "error"

# заполнение квадрата пустотами

matrix = [[None for z in range(num)] for z in range(num)]

# заполнение центрального верхнего элемента квадрата

y = 0

x = num // 2

matrix[y][x] = 1

# заполнение элементов квадрата

for i in range(2, num * num + 1):

# движение по диагонали

old_x, old_y = x, y

x = (x + 1) % num

y = (y - 1) % num

# если место заполнено, то спуск вниз

if not matrix[y][x] is None:

x = old_x

y = (old_y + 1) % num

matrix[y][x] = i

return matrix

except:

return "error"

TEST_LAB6_VAR15()

N = getting_n()

while N % 2 == 0:

print("Ошибка. N - нечетное целое число")

N = getting_n()

magic = LAB6_VAR15(N)

# вывод магического квадрата

for i in range(N):

for j in range(N):

print(magic[i][j], end=' ')

print()

Описание тестового набора

Таблица 2 представляет собой описание всех тестовых случаев.

Таблица 2 - Описание тестового набора

Описание тестового случая	Входные данные	Ожидаемые результаты	Результат теста
Правильное вычисление и ввод данных	N = 3	[[8, 1, 6], [3, 5, 7], [4, 9, 2]]	"Тест 1 пройден"
Правильное вычисление и ввод данных (вторая проверка)	5	[[17, 24, 1, 8, 15], [23, 5, 7, 14, 16], [4, 6, 13, 20, 22], [10, 12, 19, 21, 3], [11, 18, 25, 2, 9]]	"Тест 2 пройден"
N – не целое число	‘ hello’	‘error’	"Тест 3 пройден"
N – четное число	2	‘error’	"Тест 4 пройден"

Листинг тестовых сценариев:

# тестовая функция

def TEST_LAB6_VAR15():

if LAB6_VAR15(3) == [[8, 1, 6], [3, 5, 7], [4, 9, 2]]:

print("Тест 1 пройден")

else:

print("Тест 1 не пройден")

if LAB6_VAR15(5) == [[17, 24, 1, 8, 15], [23, 5, 7, 14, 16], [4, 6, 13, 20, 22], [10, 12, 19, 21, 3], [11, 18, 25, 2, 9]]:

print("Тест 2 пройден")

else:

print("Тест 2 не пройден")

if LAB6_VAR15('hello') == 'error':

print("Тест 3 пройден")

else:

print("Тест 3 не пройден")

if LAB6_VAR15(2) == 'error':

print("Тест 4 пройден")

else:

print("Тест 4 не пройден")

Результат работы тестов до написания основной программы представлен на рисунке 2. После написания работы программы на рисунке 3.

Рисунок 2 – Работа теста, до написания основного кода

Рисунок 3 – Работа теста, после написания основного кода

Пример работы программы, где пользователь вводит все данные правильно на рисунке 4.

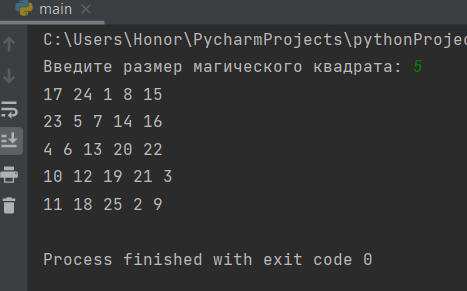
Рисунок 4 – Пример работы с правильным вводом

На рисунке 5 представлены всевозможные ошибки пользователя: где он вводит N не целое число и нечетное число. Наглядно показано, что программа заставляет пользователя вводить данные, подходящие под параметры задачи, указывает, как правильно ввести данные.

Рисунок 5 – Пример работы с неверными вводами

Выводы:

В процессе выполнения данной лабораторной работы были изучены и выполнены следующие этапы:

1) Постановка задачи. Разделил программы на чёткие этапы для более удобного просмотра кода и работы кода с помощью простых действий. Ввёл ограничения на ввод данных и рассчитал возможные завершения программы.

2) Математическая модель. Написал код с помощью математических действий, разделив задачу на простые математические действия в цикле.

3) Описание разработанной программы. По коду программы построил блочную модель программы. Выбрал наиболее подходящий способ написания кода с помощью массивов.

Благодаря данной работе закрепил свои навыки программирования, построения алгоритма решения задачи, разбив ее на несколько этапов, укрепил навыки работы с условными конструкциями. Также закрепил применение метода Test-Driven-Development.