ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., канд. техн. наук				А. В. Аграновский
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №5

СМЕШАННЫЕ АЛГОРИТМЫ 2

по курсу: ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016				Жовтяк М.О.
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2022

Вариант 15 (15 задание)

Постановка задачи

Дана функция:

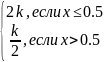F(x) = * , где и x = 0.1, 0.2…0.9.

Конечная цель программы – вычислить значение данной функции.

Входные данные: дробное число x, которое находится в пределах от 0.1 до 0.9 с шагом 0.1; и целое число K.

Выходные данные: вычисленное значение функции, выраженное в плавающем числе.

Дополнительные требования к программе не были выявлены.

Математическая модель

Дробное число x находится в пределах от 0.1 до 0.9 с шагом 0.1 согласно заданию.

Целое число K является целым числом и больше либо равно 1, так как является верхней границей суммирования в функции.

В функции присутствуют синусы и косинусы, поэтому в программы импортируются соответственные функции из библиотеки math. Также функция содержит последовательную сумму, поэтому в программе будет применен цикл for.

Описание разработанной программы

Первым делом, программа с помощью функций input_K и input_x принимает входные данные для работы. Эти значения проверяются на соответствие заданным условиям, описанным в математической модели. Основная часть программы оформлена в отдельной функции LAB5_VAR15. Согласно заданию, необходимо вычислить значение функции. Вычисление функции разделено на две логические части: сначала вычисляется дробь, в которой присутствуют синусы и косинусы; потом вычисляется последовательная сумма, оформленная в виде цикла согласно заданию. Эти две части умножаются и результат, округленный до двух знаков после запятой (для простоты чтения и сравнения в тесте), выводится в качестве выходного значения.

Таблица 1 демонстрирует список используемых переменных.

Таблица 1 - Описание переменных

Имя переменной	Тип переменной	Назначение переменной
K	int	Параметр заданной функции
x	float	Параметр заданной функции
num	int(1) и float(2)	Промежуточная переменная для записи K (1) и x (2)
f	float	Вычисление дробной части функции
s	float	Вычисление части функции с последовательной суммой
a	float	Один из параметров последовательной суммы
r	float	Переменная, хранящая итоговый результат

Описание алгоритма работы программы представлено в виде блок схемы на рисунке 1.

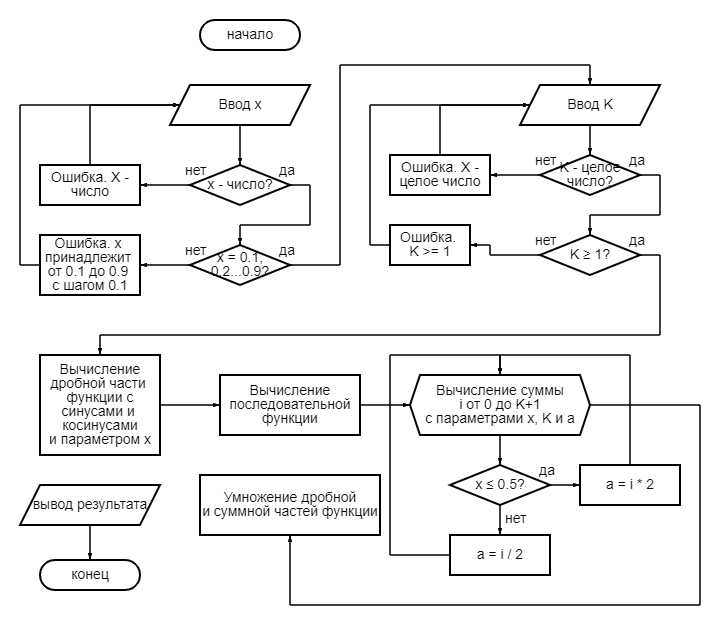
Рисунок 1 – Блок-схема алгоритма

Вычислительная сложность реализованного алгоритма в нотации O() является линейной (O(n)).

Код программы:

from math import sin, cos

# задача K

def input_K():

while True:

try:

num = int(input("Введите K: "))

except:

print("Ошибка. K - целое число")

continue

return num

# задача x

def input_x():

while True:

try:

num = float(input("Введите x: "))

except:

print("Ошибка. x - число")

continue

return num

#основная функция

def LAB5_VAR15(x, K):

# проверка входимых значений

try:

if K < 1 and not K.isdigit():

return "error"

if x == 0.1 or x == 0.2 or x == 0.3 or x == 0.4 or x == 0.5 or x == 0.6 or x == 0.7 or x == 0.8 or x == 0.9:

pass

else:

return "error"

except:

return "error"

try:

# вычисление дроби

f = (sin(x)+2)/(3+cos(x))

# вычисление последовательной суммы

s = 0

for i in range(K+1):

if x <= 0.5:

a = 2 * i

else:

a = i / 2

s += a * (x**i)

return round(f*s, 2)

except:

return "error"

#TEST_LAB5_VAR15()

x = input_x()

while x != 0.1 and x != 0.2 and x != 0.3 and x != 0.4 and x != 0.5 and x != 0.6 and x != 0.7 and x != 0.8 and x != 0.9:

print('Ошибка. x принадлежит от 0.1 до 0.9 с шагом 0.1')

x = input_x()

K = input_K()

if K < 1:

print('Ошибка. K >= 1')

K = input_K()

r = LAB5_VAR15(x, K)

print(r)

Описание тестового набора

Таблица 2 представляет собой описание всех тестовых случаев. Входные данные представляют собой такой набор: первый список – первая последовательность чисел, второй список – вторая последовательность чисел, третья переменная – число n (количество элементов списков).

Таблица 2 - Описание тестового набора

Описание тестового случая	Входные данные	Ожидаемые результаты	Результат теста
Правильное вычисление и ввод данных	x=0.1, K=2	0.13	"Тест 1 пройден"
Неправильный ввод x	x=2, K=2	‘error	"Тест 2 пройден"
Неправильный ввод K	x=0.1, K=-1	‘error’	"Тест 3 пройден"
Входные данные – строковые значения	x=’hello’, K=’world’	‘error’	"Тест 4 пройден"
Правильное вычисление и ввод данных (вторая проверка)	x=0.5, K=5	2.28	"Тест 5 пройден"

Листинг тестовых сценариев:

# тестовая функция

def TEST_LAB5_VAR15():

if LAB5_VAR15(0.1, 2) == 0.13:

print("Тест 1 пройден")

else:

print("Тест 1 не пройден")

if LAB5_VAR15(2, 2) == 'error':

print("Тест 2 пройден")

else:

print("Тест 2 не пройден")

if LAB5_VAR15(0.1, -1) == 'error':

print("Тест 3 пройден")

else:

print("Тест 3 не пройден")

if LAB5_VAR15('hello', 'world') == 'error':

print("Тест 4 пройден")

else:

print("Тест 4 не пройден")

if LAB5_VAR15(0.5, 5) == 2.28:

print("Тест 5 пройден")

else:

print("Тест 5 не пройден")

Результат работы тестов до написания основной программы представлен на рисунке 2. После написания работы программы на рисунке 3.

Рисунок 2 – Работа теста, до написания основного кода

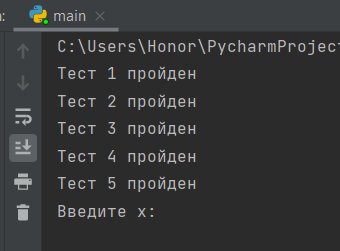
Рисунок 3 – Работа теста, после написания основного кода

Пример работы программы, где пользователь вводит все данные правильно на рисунке 4.

Рисунок 4 – Пример работы с правильным вводом

На рисунке 5 представлены всевозможные ошибки пользователя: где он вводит x не в заданном диапазоне и иное от float значение, где он вводит в K не целое число и целое число меньше 1. Наглядно показано, что программа заставляет пользователя вводить данные, подходящие под параметры задачи, указывает, как правильно ввести данные.

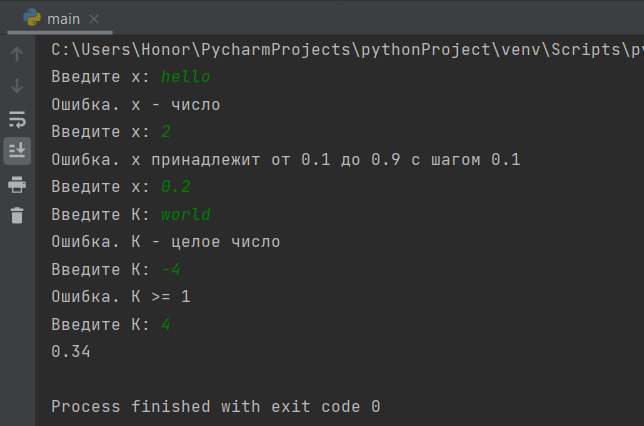
Рисунок 5 – Пример работы с неверными вводами

Выводы:

В процессе выполнения данной лабораторной работы были изучены и выполнены следующие этапы:

1) Постановка задачи. Разделил программы на чёткие этапы для более удобного просмотра кода и работы кода с помощью простых действий. Ввёл ограничения на ввод данных и рассчитал возможные завершения программы.

2) Математическая модель. Написал код с помощью математических действий, разделив задачу на простые математические действия в цикле.

3) Описание разработанной программы. По коду программы построил блочную модель программы. Выбрал наиболее подходящий способ написания кода с помощью циклов.

Благодаря данной работе закрепил свои навыки программирования, построения алгоритма решения задачи, разбив ее на несколько этапов, укрепил навыки работы с условными конструкциями. Также закрепил применение метода Test-Driven-Development.