2сем / практика

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА №3

ПРЕПОДАВАТЕЛЬ

Доцент, к.т.н.				Егоров М.Ю.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ДОМАШНЯЯ РАБОТА

Номер задачи	1.11	2.14	3.13	4.24	6.17	7.3	8.2	9.6	12.3	13.9
Ответ
Оценка в баллах

по курсу: ОБЩАЯ ФИЗИКА

СТУДЕНТ ГР. №		4016				М.О.Жовтяк
	номер группы			подпись, дата		инициалы, фамилия

Санкт-Петербург

2021

Домашняя работа по физике

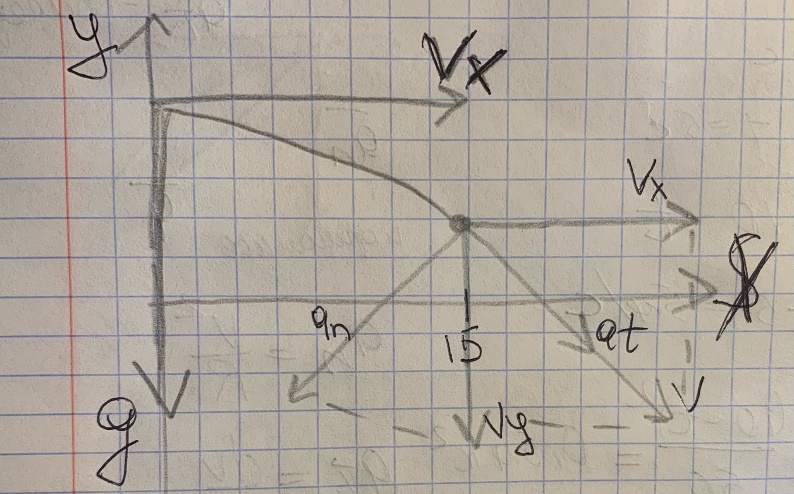
Задача 1.11

Камень брошен горизонтально со скоростью 15 м/с. Найти нормальное и тангенциальное ускорение камня через 1 с после начала движения. Сопротивление воздуха не учитывать.

Дано: v_x = 15 м/с, t = 1c. Найти: a_n, a_t

Решение:

Общая скорость - V=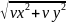 = =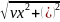 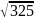м/c

Угол α – угол между вектором v_x и a_t или между a_n и v_y, тогда:

cosα = 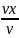sinα = =

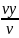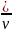
Так как происходит падение камня, то a = g.

a_n = a*cosα = g*cosα = 10 * 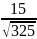= 8,3 м/c² (округлил до десятых)

a_t = a * sinα = g * sinα = 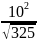= 5,5 м/c² (округлил до десятых)

Ответ: a_n = 8,3 м/c², a_t = 5,5 м/c²

Задача 2.14

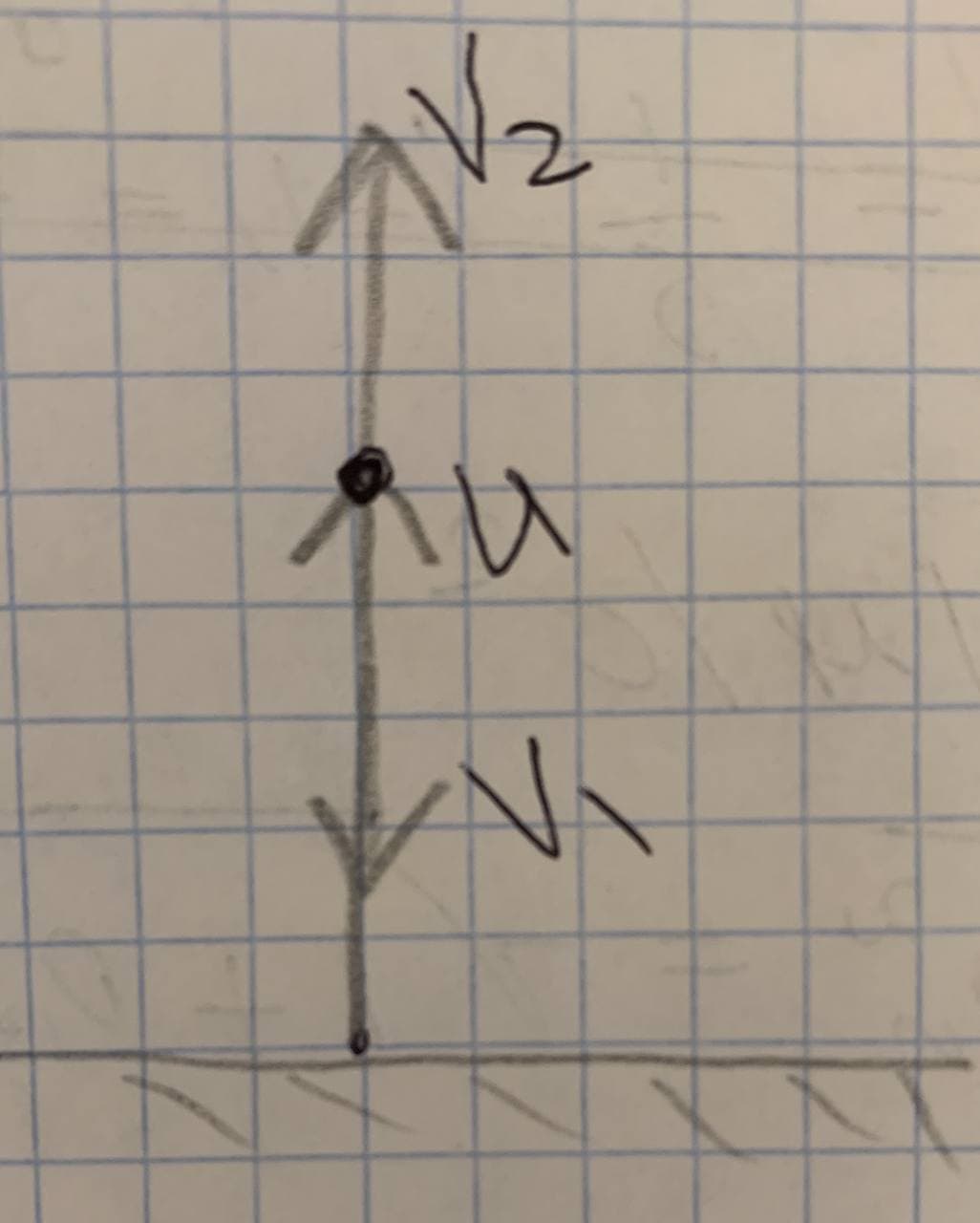
Снаряд массой 5 кг, вылетевший из орудия, в верхней точке траектории имеет скорость 300 м/с. В этой точке он разорвался

на два осколка, больший осколок массой 3 кг полетел в обратном

направлении со скоростью 100 м/с. Определить скорость второго,

меньшего осколка.

Дано: m=5кг u=300м/c m₁=3кг m₂=2кг v₁=100м/c Найти: v₂

Решение:

По закону сохранения импульса: p = p₁ + p₂

mu = m₁v₁ + m₂v₂

Так как больший осколок летит вниз, то получится:

mu = - m₁v₁ + m₂v₂

Тогда найдём v₂:

V₂ = 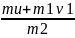= =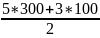 900 м/c

Ответ: v₂ = 900 м/с

Задача 3.13

Вагон массой 12 т двигался со скоростью 1 м/с. Налетев на

пружинный буфер, он остановился, сжав пружину буфера на 10 см.

Найти жесткость пружины.

Дано: m=12000кг v=1м/c x =0,1м Найти: k

Решение:

В начале поезд обладает кинетической энергией и после столкновения с пружинным буфером его кинетическая энергия переходит в потенциальную энергию пружины. Тогда:

E_к = Е_п

=

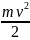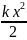
Выразив k, получим: k = 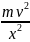= = 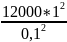120 Н/м

Ответ: k = 120 Н/м

Задача 4.24

Блок, который можно считать однородным диском массой

200 г, укреплен на горизонтальной оси. Через него перекинута нить

с укрепленными на ее концах грузами 325 г и 225 г. Нить не скользит по блоку. С каким ускорением будут двигаться грузы?

Дано: M = 200г, m₁ = 325г, m₂ = 225г. Найти: а

Решение:

a = 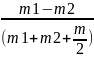* g = 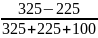* 9,8 = 1,5 м/c²

Ответ: a = 1,5 м/c²

Задача 6.17

Определить амплитуду и начальную фазу результирующего колебания, возникающего при сложении двух колебаний с одинаковыми направлениями и периодами: x1 = 0,01sin(ωt) м и x2 = 0,01sin(ωt + 0,5) м. Найти уравнение результирующего колебания.

Дано: x1 = 0,01sin(ωt)м, x2 = 0,01sin(ωt + 0,5)м. Найти: А, x(t) и φ.

Решение:

A² = (A₁)² + (A₂)² + 2A₁A₂*cos (φ₂ – φ₁) = 2 * (0,01)² * (1 + cos(0,5)) => A = 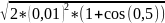= 0,0194м.

Tgφ = 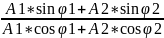= = 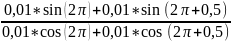0,256756

Тогда φ = 0,08π

Уравнение результативного колебания будет выглядеть так:

X(t) = A * sin (ωt + φ) = 0,0194*sin (πt + 0,08π)

Ответ: A = 0,0194м, φ = 0,08π, X(t) = 0,0194*sin (πt + 0,08π)

Задача 7.3

Логарифмический декремент затухания математического маятника 0,2. Во сколько раз изменится амплитуда колебаний за время, равное периоду Т?

Дано: ϴ = 0,2, T. Найти: .

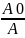Решение:

А = А₀ * e^-βt и β = 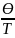. Из этих формул следует:

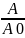= e в степени (- * t) = e^-0,2 = 0,88

= e^0,2 = 1,22

Ответ: амплитуда колебаний уменьшится в 1,22 раза.

Задача 8.2

Определить коэффициент затухания колебаний математического маятника длиной 1 м, если резонансная частота вынужденных колебаний равна 2,41 рад/с.

Дано: l = 1м, Ω_рез = 2,41рад/c. Найти: β.

Решение:

Ω_рез = =

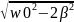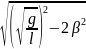
Ω_рез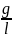² = – 2β²

β = 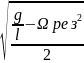= 1,41с^-1.

Задача 9.6

Стальную деталь проверяют ультразвуковым дефектоскопом, работающим на частоте 1 МГц. Отраженный от дефекта сигнал возвратился на поверхность металла через 8 мкс после испускания. Зная, что длина ультразвуковой волны 5 мм, определить, на какой глубине находится дефект.

Дано: ν = 1МГц, t = 8мкс, λ = 5мм. Найти: H.

Решение:

H = v * τ

τ = 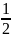* t

H = * v * t

v = λ * ν

H = * λ * ν * t = * 0,005 * 10⁶ * 8 * 10^-6 = 0,02м

Ответ: H = 0,02м.

Задача 12.3

Вычислить потенциальную энергию двух точечных зарядов 100 и 10 нКл, находящихся на расстоянии 10 см друг от друга.

Дано: q₁ = 10^-7 Кл, q₂ = 10^-8 Кл, d = 0,1м. Найти: E_п

Решение:

E_п = 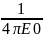* 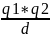= = 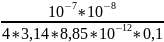8,99*10^-5 Дж.

Ответ: E_п = 8,99*10^-5 Дж.

Задача 13.9

Электрон движется вдоль силовой линии однородного электрического поля. В точке с потенциалом 100 В его скорость 6 Мм/с. Найти потенциал точки поля, в которой скорость электрона уменьшится вдвое.

Дано: v₁ = 6 Мм/c, φ₁ = 100В, v₂ = 3 Мм/c. Найти: φ₂

Решение:

Потенциальная энергия: W = W₁ – W₂ = e * U = e * (φ₁ – φ₂)

Согласно закону сохранения энергии:

Е₁ + W₁ = Е₂ + W₂

E₁ – E₂ = W₂ – W₁ = W

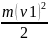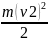- = e * (φ₁ – φ₂)

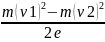φ₂ = φ₁ - = φ₁ - 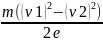= 100 - =

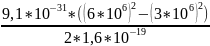= 23,3В

Ответ: φ₂ = 23,3В