lab 1 Zhovtyak

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Д.В. Куртяник
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ

ПЕРЕДАЧА ИМЁН ФУНКЦИЙ В КАЧЕСТВЕ ПАРАМЕТРОВ

по курсу: ОСНОВЫ ПРОГРАММИРОВАНИЯ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4016		21.03.2021		М.О.Жовтяк
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2021

Вариант 17

Метод определения значения определённого интеграла:

Метод прямоугольных трапеций

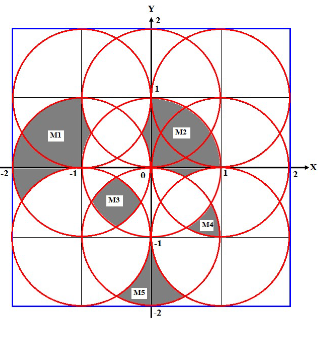
Математическая модель области М₁:

Уравнения линий, ограничивающих выделенные штриховкой области:

(x+1)² + y² <1 (правая центральная окружность)

x²+y² > 1 (область вне центральной окружности)

x² + (y-1)² >1 (область вне верхней центральной окружности)

(x+1)² + (y+1)² > 1 (область вне нижней левой окружности)

Условие попадания точки в каждую выделенную область:

Одновременное выполнение неравенств, предоставленных выше

Аналитическое выражение определения площади:

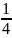площади окружности + маленький кусочек справа (с примерными подсчетами) + похожий на треугольник фигура снизу

*  * r² + 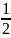* 1 * 0.433 + * 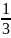* 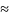1,08

Аналитический вид функций:

y = 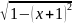[-2; -1]

y = [-2; -1,866]

y = - – 1 [-1,866; -1]

y = 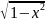+ 1 [-1; -0,866]

y = [-1; -0,866]

S = - + + +

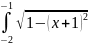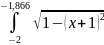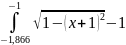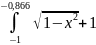1) Разделим отрезок [-2; -1] на два равных участка [-2; -1,5] и [-1,5; -1] c шагом 0.5

Получим два интеграла 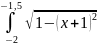и

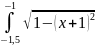
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

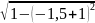( + )/2 + )*0.5 = 0,68

2) Разделим отрезок [-2; -1,866] на два равных участка [-1,933; -1,866] и [-2; -1,933] c шагом 0.067

Получим два интеграла 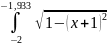и

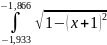
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

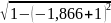( + )/2 + 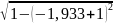)*0.067 = 0,04

3) Разделим отрезок [-1,866; -1] на два равных участка [-1,866; -1,433] и [-1,433; -1] c шагом 0.433

Получим два интеграла 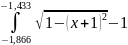и

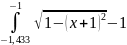
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

-( + )/2 + 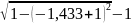)*0.433 = 0,15

4) Разделим отрезок [-1; -0,866] на два равных участка [-1; -0,933] и [-0,933; -0,866] c шагом 0.067

Получим два интеграла и

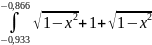
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

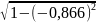(( + 1+ + + 1 + )/2 + + 1 + ) * 0,067 = 0,21

Тогда S = 0,68 + 0,04 + 0,15 + 0,21 = 1,08

Математическая модель области М2:

Уравнения линий, ограничивающих выделенные штриховкой области:

x² + y² < 1 (центральная окружность)

(x+1)²+(y-1)²> 1 (вне левой верхней окружности)

(x+1)²+(y)²> 1 (вне левой центральной окружности)

x² + (y+1)² > 1 (вне нижней центральной окружности)

(x-1)² + (y+1)² > 1 (вне нижней правой окружности)

Условия попадания точки в каждую выделенную область:

Одновременное выполнение неравенств, предоставленных выше

Аналитическое выражение определения площади:

площади окружности + 2 маленькие участки фигур снизу и слева

S = *  * r² + * * * 2 = 0,95

Аналитический вид функций:

y = [0;1]

y = + 1 [-0,134; 0]

y = [-0,134; 0]

y = – 1 [0; 0,5]

y = 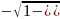– 1 [0,5; 1]

S = + + + ­

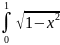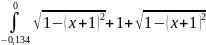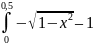1) Разделим отрезок [0;1] на два равных участка [0; 0,5] и [0,5; 1] c шагом 0.5

Получим два интеграла и

По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

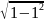( + )/2 + )*0.5 = 0,68

2) Разделим отрезок [-0,134; 0] на два равных участка [-0,134; -0,067] и [-0,067; 0] c шагом 0.067

Получим два интеграла и

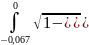
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

( + )/2 + )*0.067 = 0,21

3) Разделим отрезок [0; 0,5] на два равных участка [0; 0,25] и [0,25; 0,5] c шагом 0.25

Получим два интеграла 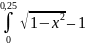и

По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

-( – 1+ – 1)/2 + 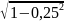– 1) *0.25 = 0,025

4) Разделим отрезок [0,5; 1] на два равных участка [0,5; 0,75] и [0,75; 1] c шагом 0.25

Получим два интеграла 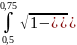и

По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

- ( + )/2 + ) *0.25 = 0,025

Тогда S = 0,68 + 0,21 + 0,025 + 0,025 = 0,94

Математическая модель области М3:

Уравнения линий, ограничивающих выделенные штриховкой области:

x² + y² < 1 (центральная окружность)

(x+1)² + y² <1 (левая центральная окружность)

(x+1)² + (y+1)² <1(левая нижняя окружность)

x² + (y+1)² < 1 (нижняя центральная окружность)

Условия попадания точки в каждую выделенную область:

Одновременное выполнение неравенств, предоставленных выше

Аналитическое выражение определения площади:

площадь окружности – 2 * площади маленьких кусочков по бокам – 3 площади треугольно подобных фигур

Площадь треугольно подобной фигуры = 1 – ¼ *r^2 – 2 *1/2*1/3*1 /2 0,048

S = *  * r² - * * * 2 – 3*0,048 = 0,4747

Аналитический вид функций:

y = [-0,866; -0,5]

y = [-0,5; -0,134]

y = – 1 [-0,5; -0,134]

y = – 1 [-0,866; -0,5]

S = +

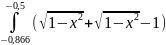1) Разделим отрезок [-0,866; -0,5] на два равных участка [-0,866; -0,683] и [-0,683; -0,5] c шагом 0.183

Получим два интеграла и

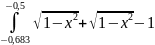
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

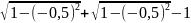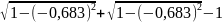( + )/2 + )*0.183 = 0,151

2) Разделим отрезок [-0,5; -0,134] на два равных участка [-0,5; -0,317] и [-0,317; -0,134] c шагом 0.183

Получим два интеграла 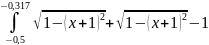и

По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

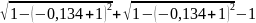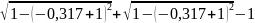( 1 + )/2 + )*0.183 = 0,151

S = 0,197 + 0,151 = 0,348

Математическая модель области М4:

Уравнения линий, ограничивающих выделенные штриховкой области:

x² + y² > 1 (вне центральной окружности)

(x-1)² + y² <1 (правая центральная окружность)

x² + (y+1)² <1 (нижняя центральная окружность)

Условия попадания точки в каждую выделенную область:

Одновременное выполнение неравенств, предоставленных выше

Аналитическое выражение определения площади:

Из квадрата вычесть четверть окружности и 2 маленьких кусочка по бокам

S = 1 – ¼ *r^2 – 2 *1/2*1/3*1 /2 0,048

Аналитический вид функций

x = 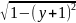[-1, -0.5]

x = 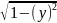+1 [-1, -0.5]

S =

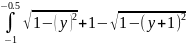
1) Разделим отрезок [-1; -0,5] на два равных участка [-1; -0,75] и [-0,75; -0,5] c шагом 0.25

Получим два интеграла 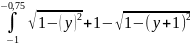и

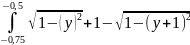
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

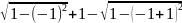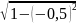(( + + 1 - )/2 + 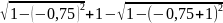)*0,25 = 0,29

Математическая модель области М5:

Уравнения линий, ограничивающих выделенные штриховкой области:

(x+1)² + (y+1)² > 1 (левая нижняя окружность)

(x -1)² + (y+1)² > 1 (правая нижняя окружность)

(x)² + (y+1)² <1 (центральная нижняя окружность)

x²+y² > 1 (вне центральной окружности)

Условия попадания точки в каждую выделенную область:

Одновременное выполнение неравенств, предоставленных выше

Аналитическое выражение определения площади:

Предположим, что эта область треугольник и найдём её площадь

½ * 1*0.866 = 0.433

Аналитический вид функций:

y = 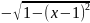- 1 [0, 0.5]

y = 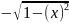- 1 [0, 0.5]

S = 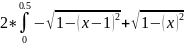(т.к. у нас две симметричные области, мы найдём площадь одной и умножим на 2)

1) Разделим отрезок [0; 0,5] на два равных участка [0; 0,25] и [0,25; 0,5] c шагом 0.25

Получим два интеграла 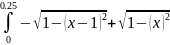и

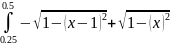
По формуле ((f (0) + f (2))/2 + f (1)) * h выходит:

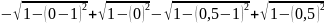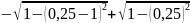(( )/2 )*0,25 = 0,2

Итоговая площадь = 0,2 * 2 = 0,4

Как будет работать программа?

Сначала вводятся координаты точки пользователем, после этого эти координаты передаются в функцию region, где определяется область, в которой находится данная точка. С нахождением области в консоль выводится номер области и в функцию main передается номер этой области. Из функции main передаем номер найденной области в функцию square, где происходят интегральные исчисления функции, которые выводятся на экран.

Код программы:

#include <iostream>

#include "math.h"

using namespace std;

int region(double x, double y)

{

if (pow(x + 1, 2) + pow(y, 2) <= 1 and pow(x, 2) + pow(y, 2) > 1 and pow(x, 2) + pow(y-1, 2) > 1 and pow(x+1, 2) + pow(y+1, 2) > 1)

{

cout << "The coordinate belongs to the M1" << endl;

return 1;

}

if (pow(x, 2) + pow(y, 2) <= 1 and pow(x + 1, 2) + pow(y - 1, 2) > 1 and pow(x + 1, 2) + pow(y, 2) > 1 and pow(x, 2) + pow(y + 1, 2) > 1 and pow(x - 1, 2) + pow(y + 1, 2) > 1)

{

cout << "The coordinate belongs to the M2" << endl;

return 2;

}

if (pow(x, 2) + pow(y, 2) <= 1 and pow(x + 1, 2) + pow(y, 2) <= 1 and pow(x + 1, 2) + pow(y + 1, 2) <= 1 and pow(x, 2) + pow(y + 1, 2) <= 1)

{

cout << "The coordinate belongs to the M3" << endl;

return 3;

}

if (pow(x, 2) + pow(y, 2) > 1 and pow(x - 1, 2) + pow(y, 2) <= 1 and pow(x, 2) + pow(y + 1, 2) <= 1)

{

cout << "The coordinate belongs to the M4" << endl;

return 4;

}

if (pow(x + 1, 2) + pow(y + 1, 2) > 1 and pow(x - 1, 2) + pow(y + 1, 2) > 1 and pow(x, 2) + pow(y + 1, 2) <= 1 and pow(x, 2) + pow(y, 2) > 1)

{

cout << "The coordinate belongs to the M5" << endl;

return 5;

}

cout << "The point doesn't belong to any region" << endl;

}

int square(int rez)

{

if (rez == 1)

{

double s1 = ((sqrt(1 - pow(-2 + 1, 2)) + sqrt(1 - pow(-1 + 1, 2))) / 2 + sqrt(1 - pow(-1.5 + 1, 2))) * 0.5;

double s2 = ((sqrt(1 - pow(-2 + 1, 2)) + sqrt(1 - pow(-1.866 + 1, 2))) / 2 + sqrt(1 - pow(-1.933 + 1, 2))) * 0.067;

double s3 = -((sqrt(1 - pow(-1.866 + 1, 2)) + -1 + sqrt(1 - pow(-1 + 1, 2)) - 1) / 2 + sqrt(1 - pow(-1.433 + 1, 2)) - 1) * 0.433;

double s4 = ((sqrt(1 - pow(-1, 2)) + 1 + sqrt(1 - pow(-1, 2)) + sqrt(1 - pow(-0.866, 2)) + 1 + sqrt(1 - pow(-0.866, 2))) / 2 + sqrt(1 - pow(-0.933, 2)) + 1 + sqrt(1 - pow(-0.933, 2))) * 0.067;

cout << "S = " << s1 + s2 + s3 + s4;

}

if (rez == 2)

{

double s1 = ((sqrt(1 - pow(0, 2)) + sqrt(1 - pow(1, 2))) / 2 + sqrt(1 - pow(0.5, 2))) * 0.5;

double s2 = ((sqrt(1 - pow(-0.134 + 1, 2)) + 1 + sqrt(1 - pow(-0.134 + 1, 2)) + sqrt(1 - pow(0 + 1, 2)) + 1 + sqrt(1 - pow(0 + 1, 2))) / 2 + sqrt(1 - pow(-0.067 + 1, 2)) + 1 + sqrt(1 - pow(-0.067 + 1, 2))) * 0.067;

double s3 = -((sqrt(1 - pow(0, 2)) - 1 + sqrt(1 - pow(0.5, 2)) - 1) / 2 + sqrt(1 - pow(0.25, 2)) - 1) * 0.25;

double s4 = -((sqrt(1 - pow(0.5 - 1, 2)) - 1 + sqrt(1 - pow(1 - 1, 2)) - 1) / 2 + sqrt(1 - pow(0.75 - 1, 2)) - 1) * 0.25;

cout << "S = " << s1 + s2 + s3 + s4;

}

if (rez == 3)

{

double s1 = ((sqrt(1 - pow(-0.866, 2)) + sqrt(1 - pow(-0.866, 2)) - 1 + sqrt(1 - pow(-0.5, 2)) + sqrt(1 - pow(-0.5, 2)) - 1) / 2 + sqrt(1 - pow(-0.683, 2)) + sqrt(1 - pow(-0.683, 2)) - 1) * 0.183;

double s2 = ((sqrt(1 - pow(-0.5 + 1, 2)) + sqrt(1 - pow(-0.5 + 1, 2)) - 1 + sqrt(1 - pow(-0.134 + 1, 2)) + sqrt(1 - pow(-0.134 + 1, 2)) - 1) / 2 + sqrt(1 - pow(-0.317 + 1, 2)) + sqrt(1 - pow(-0.317 + 1, 2)) - 1) * 0.183;

cout << "S = " << s1 + s2;

}

if (rez == 4)

{

double s = ((sqrt(1 - pow(-1, 2)) + 1 - sqrt(1 - pow(-1 + 1, 2)) + sqrt(1 - pow(-0.5, 2)) + 1 - sqrt(1 - pow(-0.5, 2))) / 2 + sqrt(1 - pow(-0.75, 2)) + 1 - sqrt(1 - pow(-0.75 + 1, 2))) * 0.25;

cout << "S = " << s;

}

if (rez == 5)

{

double s1 = ((-sqrt(1 - pow(0 - 1, 2)) + sqrt(1 - pow(0, 2)) - sqrt(1 - pow(0.5 - 1, 2)) + sqrt(1 - pow(0.5, 2))) / 2 - sqrt(1 - pow(0.25 - 1, 2)) + sqrt(1 - pow(0.25, 2))) * 0.25;

cout << "S = " << s1 * 2;

}

return 0;

}

int main()

{

int rez = 0;

double x;

double y;

cout << "Enter the coordinates of the point" << endl;

cin >> x >> y;

rez = region(x, y);

square(rez);

}

Скриншоты работы программы:

Область М₁:

Область М₂:

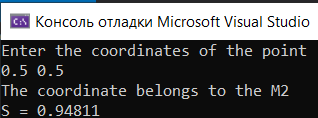
Область М₃:

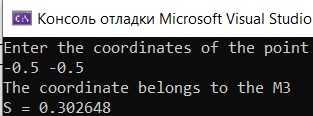
Область М₄:

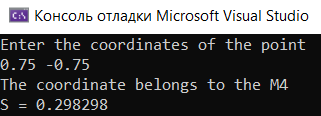
Область М₅:

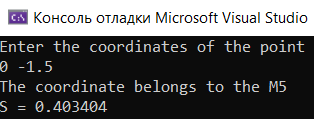
Ни одна область:

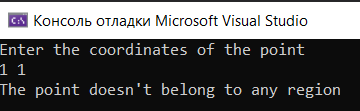
Вывод: я изучил методы передачи имён функций в качестве параметров других функций; изучил методы нахождения значения определённых интегралов функций на заданном отрезке и с заданной точностью; отточил навыки процедурного программирования на языке C/С++ при решении задач с использованием рекурсивных функций.