Жовтяк Максим логика

№1

Построить МТ, которая к заданному натуральному десятичному числу прибавляет 1. Начальная конфигурация стандартная. Например,

241q₁7 ⇒ 241q₀8

58q₁9 ⇒ 5q₀90

1 вариант

Как работает алгоритм:

Если число после “ q” меньше 9, то прибавляем 1 и остаёмся в этом же месте, если число перед “q” равно 9, заменяем его на 0, идём влево и заменяем число по нашим командам

q₁0 ⇒ q₀1S

q₁ 1 ⇒q₀2S

q₁ 2 ⇒q₀3S

q₁ 3 ⇒q₀4S

q₁ 4 ⇒q₀5S

q₁ 5 ⇒q₀6S

q₁ 6 ⇒q₀7S

q₁ 7 ⇒q₀8S

q₁ 8 ⇒q₀9S

q₁ 9 ⇒q₁0L

№2

Построить МТ, которая к заданному натуральному десятичному числу прибавляет 2. Начальная конфигурация стандартная.

1 вариант

Как работает алгоритм:

Если число после “ q” меньше 8, то прибавляем 2 и остаёмся в этом же месте, если число перед “q” равно 8, заменяем 8 на 0, идём влево, прибавляем к числу 1, если число перед “q” равно 9, заменяем 9 на 1, идём влево, прибавляем к числу 1.

q₁0 ⇒ q₀2S

q₁ 1 ⇒q₀3S

q₁ 2 ⇒q₀4S

q₁ 3 ⇒q₀5S

q₁ 4 ⇒q₀6S

q₁ 5 ⇒q₀7S

q₁ 6 ⇒q₀8S

q₁ 7 ⇒q₀9S

q₁ 8 ⇒q₂0L

q₁ 9 ⇒q₂1L

Прибавление единицы

q₂0 ⇒ q₀1S

q₂ 1 ⇒q₀2S

q₂ 2 ⇒q₀3S

q₂ 3 ⇒q₀4S

q₂ 4 ⇒q₀5S

q₂ 5 ⇒q₀6S

q₂ 6 ⇒q₀7S

q₂ 7 ⇒q₀8S

q₂ 8 ⇒q₀9S

q₂ 9 ⇒q₂0L

№3

sg(x) =

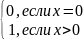
1. для стандартной начальной конфигурации

sg(x) = 0 = O(x) (заменяем все единица на 0)

Если q₁ изначально стоит перед 0,значит в числе нет единиц и мы сразу останавливаемся

q₁0 ⇒ q₀0 S

Если q₁ изначально стоит перед 1, мы сдвигаемся вправо и проверяем, стоит ли там 1, если стоит, то возвращаемся в начало последовательность единиц и убираем первую единицу, так делаем пока не останется одна единица

МТ для S(x) = 1

q₁ 1 ⇒q₂ 1 R

q₂1 ⇒ q₃1 L

q₃ 1 ⇒ q₁0 R

q₂0 ⇒ q₀ 0 S

Соединим функции O(x) и S(x)

q₁¹ 0 ⇒ q₀¹ 0 S

q₁² 1 ⇒q₂ 1 R

q₂1 ⇒ q₃1 L

q₃ 1 ⇒ q₁0 R

q₂0 ⇒ q₀² 0 S

2. для правильного вычисления функции

Так как начальная конфигурация выглядит так q₁01^x0 , теперь нам нужно проходить один дополнительный, начальный ноль и возвращаться обратно

sg(x) = 0 = O(x) (заменяем все единица на 0)

q₁ 0 ⇒ q₂ 0 R

q₂0 ⇒ q₀0 L

Если стоят два нуля подряд, то единиц нет.

МТ для S(x) = 1

q₁ 0 ⇒q₁ 0 R

q₁ 1 ⇒q₂ 1 R

q₂1 ⇒ q₃1 L

q₃ 1 ⇒ q₁0 R

q₂0 ⇒ q₄ 0 L

q₄ 1 ⇒ q_­0 1 L

Соединим функции O(x) и S(x)

q₁¹ 0 ⇒ q₂¹ 0 R

q₂¹ 0 ⇒ q₀¹ 0 S

q₁² 0 ⇒q₁² 0 R

q₁² 1 ⇒q₂ 1 R

q₂1 ⇒ q₃1 L

q₃ 1 ⇒ q₁0 R

q₂² 0 ⇒ q₄ 0 L

q₄ 1 ⇒ q_­0² 1 L

Примеры

а)

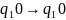
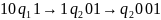
б)