september work

Жовтяк Максим, группа 4016, ГУАП

ВАРИАНТ №17

ЗАДАНИЕ ПО МАТРИЦАМ

Дано: А , B , E

1) Для того, чтобы перемножить между собой две матрицы, необходимо первую матрицу поделить на строки, а вторую поделить на столбцы. Затем необходимо каждую строку первой матрицы умножить на каждый столбец второй матрицы. Далее полученный числа складываем между собой и записываем в новую матрицу

А *B =AB

2) B А =BA

3) Вычитание матриц происходит по принципу: из элемента первой матрицы вычитается элемент второй матрицы с теми же координатами. Сложение проходит ровно по такому же принципу.

AB BA =0 – нулевая матрица

4) А³=А²*А= А * А *A= E

5) Попробуем найти закономерность для А²⁰²⁰. Мы уже выяснили, в п.4, что А³=А, тогда А⁴=А³*А=А*А=А², в п.4 мы тоже узнали, что А²=Е, то есть выходит, что А⁴=Е. Давайте вычислим А⁵=А⁴*А, так как мы знаем, что А⁴=Е, то А⁵=Е*А=А.

Чётко прослеживается, что чётные степени матрицы А равны единичной матрице, а нечетной – самой А. Так как степень 2020 – чётная, то:

А²⁰²⁰=Е

6) Е-А-А²+А³

В п.5 мы выяснили, что чётная степень матрицы А равна Е, а нечётная – самой А, тогда выражение примет следующий вид:

Е-А-А²+А³=Е-А-Е+А=Е-Е+А-А=0

Вывод: в этом задание я научился работать с матрицами, умножать, вычитать и складывать их, а также возводить матрицы в любую степень.

ЗАДАНИЕ ПО ВРАЩЕНИЮ КУБА

f=S_OO2

1) Посмотрим куда переходят точки при вращении и определим матрицу данного поворота S_OO2 куба

М₁=H₁ => M₁=F₁ (-1, 0, 0)

M₂=G₁ => M₂=E₁ (0, -1, 0) ↔ X

M₃=O₂ => M₃=M₃ (0, 0, 1)

2) Перестановка диагоналей:

AC₂(1) => CA₂(3)

BD₂(2) => DB₂(4)

CA₂(3) => AC₂(1)

DB₂(4) => BD₂(2)

Тогда отображение перестановки выглядит так:

3) Обратное вращение:

f=S_OO2 f^-1=S_OO2

f^-1=S_OO2: М₁=H₁ => M₁=F₁ (-1, 0, 0)

M₂=G₁ => M₂=E₁ (0, -1, 0) ↔ X^-1

M₃=O₂ => M₃=M₃ (0, 0, 1)

Можно проследить, что при, как и при прямом, так и обратном повороте куба по оси 4-го порядка на 180 градусов, куб вернется в то же положение. На всякий случай всё равно выполним проверку.

F = E

4) Отобразим на рисунке переход плоскости ACB₂ при повороте f=S_OO2

A => C

C => A

B₂ => D₂

КОМПЛЕКСНЫЕ ЧИСЛА. 5 ЗАДАНИЙ

Комплексное число записывается в виде: z = a+bi, где а – действительная часть

числа, b – мнимая часть числа, I – мнимая единица.

Складываются/вычитаются комплексные числа по следующему принципу:

действительная часть с действительной, мнимая с мнимой.

Умножаются комплексные числа по правилу раскрытия скобок при

умножении двух скобок, т.е. каждое число умножается на каждое другое число.

Делятся комплексные числа по следующему правилу: числитель и

знаменатель умножается на число, сопряженное знаменателю (т.е. если

знаменатель имеет вид z = a+bi, то число сопряженное ему будет z = a-bi.

Сопряженное число – это просто число, симметричное относительно оси 0х

данному числу)

1) Z1=4+i z₂=-1+3i

Сложение:

Z₁+z₂= (4+i) + (-1+3i) =3+4i

Умножение

Z₁*z₂= (4*(-1)-1*1) + (4*3+ (-1)*1) i=-7+11i

Возведение в квадрат:

Z₁²=z₁*z₁= (4*4-1*1) + (4*1+4)i=15+8i

Частное (знак означает вектор над переменной):

=

2) Записать в тригонометрической форме:

z=3=3+0i

Запись комплексного числа в виде Z = r(cos φ + isin φ) является представлением

этого комплексного числа в тригонометрическом виде.

Такая запись комплексного числа удобна при умножении одного комплексного

числа на другое. При умножении двух комплексных чисел модули

перемножаются, а аргументы складываются.

Также такая запись удобна при возведении комплексного числа в n-ую

степень. При возведении комплексного числа модуль числа возводится в -ую

степень, а аргументы умножаются на n.

r= =3

Угол: tg = 0 =>

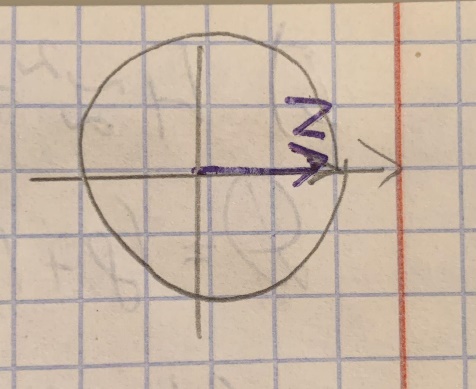
z=3+0i=3(cos2π+isin2π)

3) Возвести в степень:

z⁴³=(-1+i)⁴³

R= =

Угол: tg => -

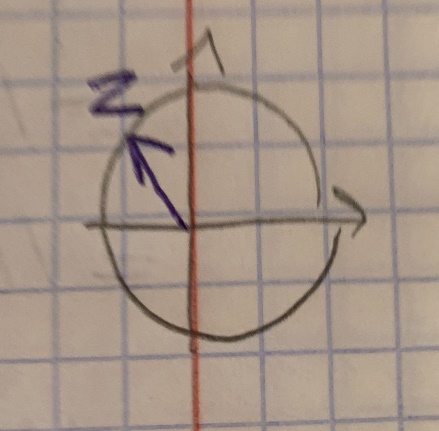
z⁴³= ( ) ⁴³(cos (-- )⁴³(cos(

4) z=

R =

Угол: tg - =>

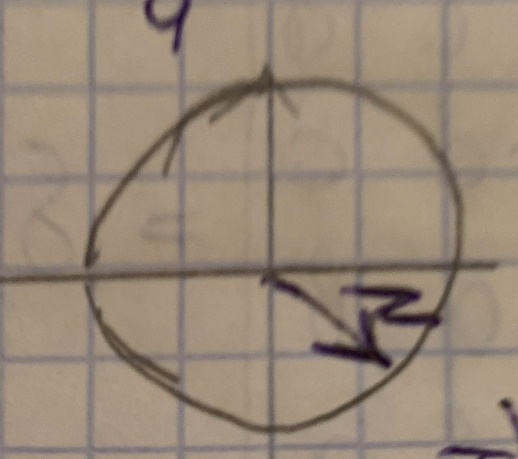
Тригонометрическая форма: z=2(cos (

Корни:

Z₀ = (cos (

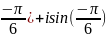
Z₁= (cos ( (cos ( )

5) 4z²+(8+16i)z-27+24i=0

D = (8+16i)²-4*4(-27+24i)=64+256i+256i²-16(-27+24i)=16(4+16i+16i²+27-24i)=16(15-8i)

Z₁₂=

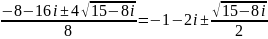
КОМПЛЕКСНЫЕ ЧИСЛА. АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ

1. Записать в тригонометрическом виде: z = 3-i

R= ²+ ²)=2

Угол: tg = =>

Приводим к тригонометрической форме:

z= 2 (cos( + isin( )

2) z =

Приведём числитель и знаменатель к тригонометрической форме в заданной степени:

1. = )²) = 4

Угол: tg = = =>

Приводим к тригонометрической форме:

z= 4¹⁰(cos( + isin( )

Используем формулу Муавра:

z¹⁰=4¹⁰(cos( + isin( )

2. = )²) = 4

Угол: tg = - = =>

Приводим к тригонометрической форме:

z= 4(cos( + isin( )

Используем формулу Муавра:

Z⁵=4⁵(cos( + isin( )

Вернёмся к нашей дроби и вычислим значение выражения:

Z= =4⁵* =-4⁵* =-4⁵*1=-1024

3) z=

R= = 4

Угол: tg = - =>

Приведем к тригонометрической форме:

z=4(cos(

Корни:

Z₀ =

Z₁ =

Z₂ =

РЕШЕНИЕ КВАДРАТНЫХ И КУБИЧЕСКИХ УРАВНЕНИЙ В ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ

1) z²-8z+41=0

D=64-4*1*41=-100

При решении квадратных уравнений, получая дискриминант, который меньше нуля, стоит знать, что уравнение имеет два мнимых решения, а не имеет их вообще, как преподаётся в школе.

Z₁₂= = =4

2) z³-7z²+40z-34=0

Так как сумма коэффициентов равна 0:

a+b+c+d=1-7+40-34=0,

то первый корень z₁=1

По схеме Горнера:

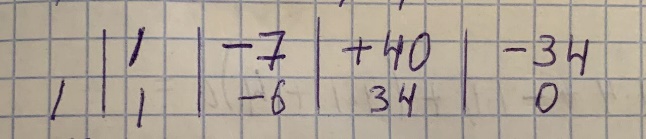
Выходит, что:

(z-1)(z²-6z+34)=0

Z²-6z+34=0

D=36-4*1*34=-100

Z₂₃=