
Tensizliklerdi dalillew usillari
.pdf

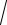 (a b)(c d )
(a b)(c d ) 
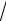 ab
ab 
 cd
cd
Sheshiliwi. Qarsısınan uyǵarıp qarayıq, yaǵnıy a,b,c,d lardıń mánisleriniń ǵeypara toparları ushın, mına teńsizlik durıs boladı deyik:

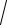 (a b)(c d )
(a b)(c d ) 

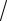 ab
ab 
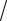 cd
cd
Bul teńsizliktiń eki jaǵin da kvadratqa kóteremız. Sonda mınaǵan iye bolamız:
|
|
|
|
|
|
|
ab bc ad cd |
ab 2 |
abcd cd . |
||
Bunnan |
ab ad |
|
|
|
|
hám bunnan keyin |
|
bc ad |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
||
biraq bul, teris emes bc hám ad sanları ushın duzilgen Koshi teńsizligine qaramaqarsı keledı.
Demek biziń bulay dep uyǵarıwımız nadurıs eken , yagnıy a ,b, c ,d lardıń teris emes qálegen mánisleri ushın, mına teńsizlik durıs eken :

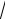 (a c)(b d)
(a c)(b d) 
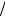 ab
ab 
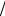 cd
cd
2-mısal. Tómendegi teńsizlikti dalilleń :
cos( ) cos( ) cos2 .
Sheshiliwi. Qarsısınan uyǵarip qarayıq, yaǵnıy qandayda bir menen bar bolıp , olar ushın mına teńsizlik orınlanadı dep uyǵayıq:
|
cos( ) cos( ) |
|
|
||||||
|
cos( ) cos( ) |
cos 2 cos 2 |
|
||||||
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
hám |
cos2 |
1 cos 2 |
|
|
|
|
|
||
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
||
formulalarınan paydalanıp, mınaǵan iye bolamız: |
|
|
|||||||
|
|
cos 2 cos 2 |
|
1 cos 2 |
, |
|
|||
|
|
|
|
|
|
|
|
||
|
2 |
|
|
2 |
|
|
|||
bunnan |
cos 2 >1 kelip shıǵadı. Durısında da β nıń qálegen mánislerinde |
||||||||
cos 2 1 bolatuǵın bizler qarama-qarsılıqqa kelip jolıqtıq. Demek , biziń
joqarıdaǵi |
úyǵarıwımız |
nadurıs eken, al sonın |
ushin da |
cos( ) cos( ) cos2 |
cos( ) cos( ) cos2 |
teńsizligi |
|
durıs teńsizlik eken. |
|
|
|
Teńlemelerdi sheshiwde teńsizliklerdi qollanıw. Meyli f (x) g(x) teńlemesin sheshiw kerek bolsın deyik, hám sonıń menen qatar qandayda bir A
degen san bar bolıp, ol san bir waqıttiń ózinde y f (x) funktsiyasınıń eń ulken mánisi hám y g(x) funktsiyasınıń eń kishi mánisi bolıp esaplansın deyik .
sonda f (x) g(x) teńlemesiniń korenleri bolıp f (x) A, g(x) A teńlemelerdi funksiyonal usılda sheshiwdiń dara jaǵdayı boladı.
12
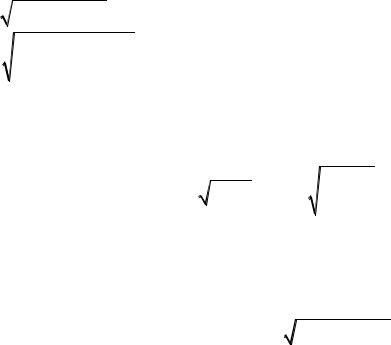
2-Misal. Teńlemeni sheshiń. x2 |
1 |
2 (x 1)4 |
|
|||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
Sheshiliwi. teńlemenińshep jaǵi ushın x 0 |
bolǵan ,barlıq mánislerde |
||||||||||
x2 |
1 |
2 |
|
|
teńsizligi, |
oń jaǵi ushin |
ondaǵı |
x tıń qálegen mánisinde |
||||
x2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (x 1)4 |
2 teńsizligi orınlanadı. Demek berilgen teńlemeniń kórenleri bolıp |
|||||||||||
, x 1 |
x2 |
1 |
2 hám |
2 (x 1)4 |
2 |
teńlemeleriniń ulıwma korenleri |
||||||
|
x2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
esaplanadı. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
x2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
teńlemesinen |
x1 1, x2 1 di tabamız. 2 (x 1)4 2 teńlemesinen x 1 di |
|||||||||||
tabamız. Bul teńlemelerdiń ulıwma bir koreni bolıp , x 1 mánisi esaplanadı. Ol koren berilgen teńlemeniń birden-bir koreni boladı.
2-§. Orta mánisler arqali teńsizliklerdi dálillew
Ayırım teńsizliklerdi dálillewde teńsizliklerdi qandayda bir almastırıwlar járdeminde dálilleymız. Bunday almastırıwlar teńsizlikde berilgen ózgeriwishlerdıń orta mánisleri arqalı ámelge asırıladı.
Orta mánisler oń sanlar izbe-izligi ushın
- A |
a1 |
|
|
a2 ... an |
orta arifmetikalıq mánis |
||||||||
|
|
|
|
|
|
|
|
||||||
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- G n |
|
a a .... a |
orta geometriyalıq mánis |
||||||||||
n |
|
|
|
1 |
2 |
n |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
- K |
|
|
|
|
|
a2 |
a2 |
... a2 |
orta kvadratlıq mánis |
||||
|
|
|
1 |
2 |
|
n |
|
||||||
n |
|
|
|
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Nn |
|
|
|
|
|
n |
|
|
orta garmonikalıq mánis |
||||
|
|
||||||||||||
a 1 a 1 |
... a 1 |
||||||||||||
|
|
|
|
|
1 |
2 |
|
n |
|
||||
Máselen a1 , a2 oń sanlar ushın joqarıdaǵı orta mánisler tómendegishe anıqlanadı:
|
|
a a |
|
|
|
|
|
|
|
|
|
|
|
a1 |
a2 |
|
|
|
|
|
2a a |
||
|
A |
, G |
|
a a , |
|
|
|
|
|
|
|
|
|
||||||||||
|
1 2 |
|
|
K |
|
1 |
2 |
|
, N |
|
|
1 2 |
|
||||||||||
|
|
|
|
|
|
a2 |
a2 |
||||||||||||||||
|
2 |
2 |
2 |
1 2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
Orta mánislerdi bir-biri menen tómendegishe teńsizliklerge alıp kelseń |
||||||||||||||||||||||
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
Orta arifmetikalıq hám orta geometrik mánisler ushın Koshi teńsizligi |
||||||||||||||||||||||
|
orınlı |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 a2 |
... an |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
n a a .... a |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
n |
|
|
|
1 |
|
2 |
|
|
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
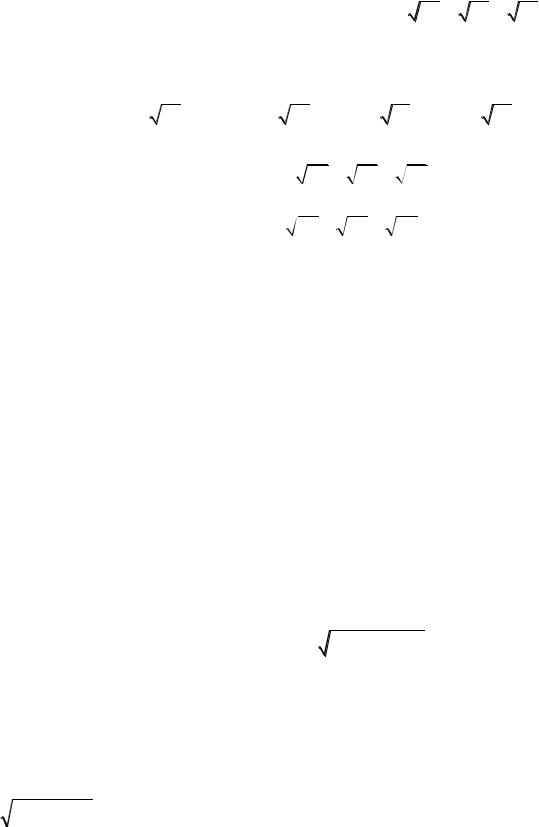
Yaǵniy An Gn hám An Gn teńlik tek ǵana a1 a2 ... an teńlik bolǵanda
orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1-mısal. Eger a 0,b 0,c 0 |
bolsa a b c |
ab bc ac teńsizlikti |
||||||||||||||||
dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Sheshılıwı: |
Teńsizliktı dálillew ushın tómendegishe úsh teńsizlikdı dúzıp |
|||||||||||||||||
alamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a b |
|
|
|
|
|
|
|
|
|
|
|||||||
|
ab, a b 2 |
|
ab,b c 2 bc,a c 2 ac, |
|||||||||||||||
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
teńsizliklerdiń qosındısınan
2(a b c) 2(
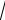 ab
ab 
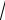 bc
bc 
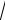 ac)
ac)
nátiyjede
(a b c) (
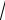 ab
ab 
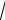 bc
bc 
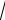 ac)
ac)
teńsizlik payda boladı, eger a b c bolsa teń boladı. Teńsizlik dálillendi. 2-mısal. x, y 0 bolsa, x2 y2 1 xy x y teńsizlikti dálilleń. Sheshılıwı: Teńsizlikdı apıwayılastıramız
x2 y2 1 xy x y |
x2 |
|
x2 |
|
y2 |
|
y2 |
|
1 |
|
1 |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
2 |
2 |
|
2 |
|
2 |
||||
|
x |
2 |
|
|
y |
2 |
xy, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y, |
x2 y2 1 xy x |
y. |
|
|
|
|
|||||||
2 |
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
2 |
|
|
1 |
x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
teńsizlik dálillendi.
2) Orta geometrik hám orta garmonikalıq mánisler G a H a teńsizligi orınlı bolıwın tekseremız.
Dálili.
a1 a2 ... an |
|
|
|
|
|
n a |
a |
.... a |
|||
|
|||||
n |
1 |
2 |
n |
||
|
|
|
|
||
Koshi teńsizliginen paydalanip
x2 y2 1
arasındaǵı teńsizlik.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
H (a) 1 |
|
|
|
|
|
|
|
n |
|
|
|
|
a1 |
a2 |
... an |
|
|
||
1 |
|
1 |
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
... |
|
|
|
|
n |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
a1 |
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
|
|
|
|||||
|
|
|
G |
a 1 |
|
|
|
|
|
|
|
|
|
|
|||||
n a 1a 1...a 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
1 2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Teńsizlikke iye bolamız. Egerde a1 a2 ... an |
bolsa G a H a teń boladı. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
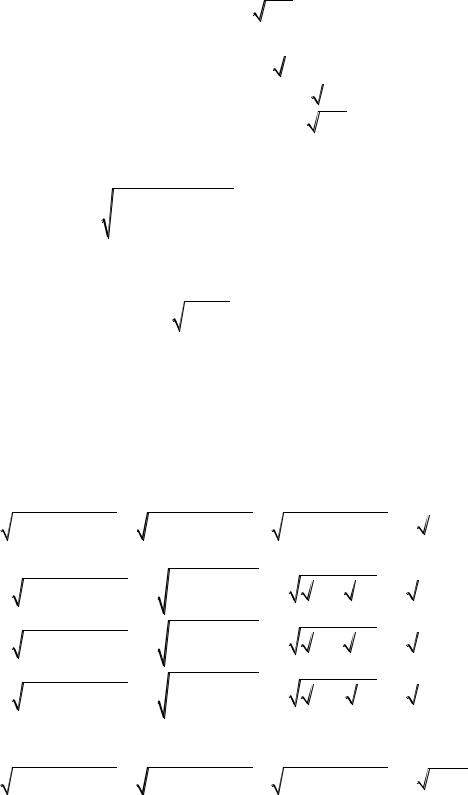
3-mısal. Eger a,b,c 0 |
bolsa |
|
|
3 |
|
|
|
|
a b c |
teńsizliktı dálilleń. |
|
|
1 |
1 |
1 |
|
|
||||||
|
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
c |
|
|
|
|
||
|
|
1 |
|
1 |
|
1 |
|
|
Sheshılıwı : Teńsizliktı kóbeytsek |
9 a b c |
|
|
|
|
|
|
, de bunnan |
|
|
|
||||||
|
a |
|
b |
|
c |
|
||
a b c 33 |
|
|
|
||||||||
|
abc |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
3 |
|
|
1 |
||
|
|
|
|
|
|
|
|||||
|
b |
c |
3 |
|
|
||||||
|
abc |
||||||||||
a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
9 3 abc |
|
||||
a b c |
|
|
|
|
|
|
|
|
|
|
|
9. |
|
b |
|
|
|
|
|
||||||
|
|
|
abc |
|||||||||
a |
|
|
c |
|
3 |
|
||||||
3) Orta arifmetik hám orta kvadratlıq mánisler arasındaǵı teńsizlık. |
||||||||||
K |
a A a teńsizlik orınlı bolıwın dálilleymiz. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
a2 |
... a2 |
|
|
a a |
... a |
|
|
|
|
1 |
2 |
n |
|
1 2 |
n |
|
|
|
|
|
|
|
n |
|
n |
|||
|
|
|
|
|
|
|
|
|||
Dálillew: Teńsizlikti dálillew ushın Koshi teńsizliginen paydalanamız 1 i j n boyınsha teńsizlikti jazamiz.
|
|
|
|
a2 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
i |
j |
a2 |
a2 |
|
|
a2 |
a |
2 2a a |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
j |
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
i |
j |
|
|
|
i |
|
j |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Usı boyınsha tómendegi teńlik arqalı korsetemiz. |
|
|
|
|
|
|
||||||||||||||||
|
a1 a2 ... a3 2 a12 a22 |
|
... an2 2 aia j |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
1 i j n |
|
n |
||||
1 |
2 |
|
|
n |
|
i |
|
|
1 |
2 |
|
|||||||||||
|
a2 a2 |
... a2 |
|
|
|
a2 |
a2 |
n |
a2 |
a2 ... a2 . |
||||||||||||
|
|
|
|
|
|
|
|
|
1 i j n |
|
|
|
|
|
|
|
|
|
|
|
||
Egerde a1 a2 ... an |
|
bolsa K a A a teńlik kelip shıǵadı. |
||||||||||||||||||||
4-mısal. Eger |
a 0,b 0,c 0, d 0 bolsa, tómendegi teńsizliktı dálilleń. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a b |
c d |
|
a c |
b d |
a d |
b c |
6 4 abcd |
||||||||||||||
Sheshılıwı: Koshi teńsizligine paydalanıp tómendegishe teńliklerdi dúzemiz.
|
|
|
|
|
|
|
|
|
|
a b |
|
|
|
c d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a b |
c d |
|
|
2 |
|
|
|
2 |
|
|
ab |
|
cd 2 4 |
abcd |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
a c |
|
|
b d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
a c |
b d |
|
|
2 |
|
|
|
2 |
|
|
ac |
bd 2 4 |
abcd |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
a d |
|
|
b c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
a d |
b c |
|
|
2 |
|
|
|
2 |
|
|
ad |
|
bc 2 4 |
abcd |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Endi teńliklerdi qosamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Nátiyjede |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
a b |
c d |
|
|
a c |
b d |
|
a d |
b c 6 4 abcd |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
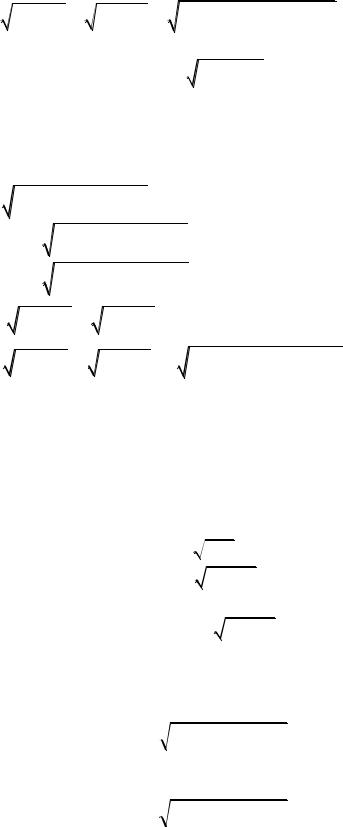
kelip shıǵadı. Teńsizlik dálillendi.
5-mısal. a1,a2 ,b1,b2 sanları ushın tómendegi teńsizlikti dálilleń.
|
|
|
|
|
|
|
|
2 b b 2 . |
|
a2 |
a2 |
b2 |
b2 |
|
a a |
2 |
|||
1 |
2 |
1 |
2 |
|
1 |
1 |
2 |
||
Sheshılıwı: teńsizliktı dálillew ushın Koshi teńsizliginen paydalanamız.
|
|
|
|
|
|
|
|
|
a2b2 |
a2b2 |
2 a2b2a2b2 |
||||||
1 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
|
|
|
|
|
|
|
a2b2 |
a2b2 2 |
|
a b a b |
|
2a b a b |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
2 |
1 |
|
|
|
|
|
|
1 |
1 |
2 |
2 |
|
|
|
|
1 |
1 |
2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a2b2 |
a2b2 |
a2b2 |
a2b2 |
a2b2 |
a2b2 |
2a b a b |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
2 |
2 |
|
2 |
|
|
1 |
|
2 |
|
2 |
1 |
|
|
|
1 |
1 |
|
|
2 |
|
2 |
|
|
1 |
1 |
2 |
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
a2 |
a2 |
b2 b2 |
|
a b a |
b 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
1 |
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
a2 a2 |
|
b2 |
b2 |
|
|
|
|
|
a b a b |
|
a b a b |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
1 |
2 |
2 |
|
|
|
|
1 |
1 |
|
2 |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a b a b |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 a2 |
a2 |
|
b2 |
|
b2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a b a b |
|
||||||||||||||||||||||
a2 |
a2 |
b2 |
b2 |
2 a2 |
a2 |
|
b2 |
|
b2 |
|
|
|
a2 |
a2 |
|
b2 |
b2 |
|||||||||||||||||||||||||||||||
1 |
2 |
1 |
|
2 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
2 |
|
|
|
1 |
|
2 |
|
1 |
1 |
2 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 a1 b1 2 a1 b2 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
a12 a22 |
b12 b22 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a1 b2 |
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
a12 a22 |
b12 b22 |
|
|
|
a1 b1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Teńsizlik |
kelip shıǵadı. |
Egerde |
a1b2 a2b1 |
|
bolsa |
teńlik |
orınlı |
|
boladı. |
|||||||||||||||||||||||||||||||||||||||
Teńsizlik dálillendi.
6-mısal. Eger a 0,b 0,c 0 sanları bar bolsa,
a b c a2 b2 c2 9abc
teńsizligin dálilleń.
Sheshılıwı: Koshi teńsizligi boyınsha tómendegishe teńsizliklerdi dúzemiz. a b c 33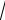 abc
abc
a2 b2 c2 33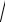 a2b2c2
a2b2c2
Eki teńsizlikdi oń hám shep jaqlarin bir-birine kóbeytemiz. Nátiyjede
a b c a2 b2 c2 93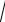 a2b2c2 9abc
a2b2c2 9abc
Nátiyjede joqarıdaǵı biz dálillemekshi bolǵan teńsizlik kelip shıǵadı. Teńsizlik dálillendi.
7-mısal. Eger x 0, y 0, z 0 bolsa
xy yz zx 
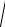 3xyz x y z
3xyz x y z
teńsizlikti dálilleń.
Sheshılıwı:
xy yz zx 
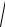 3xyz x y z berilgen teńsizliktı kvadratqa kóteremiz.
3xyz x y z berilgen teńsizliktı kvadratqa kóteremiz.
16
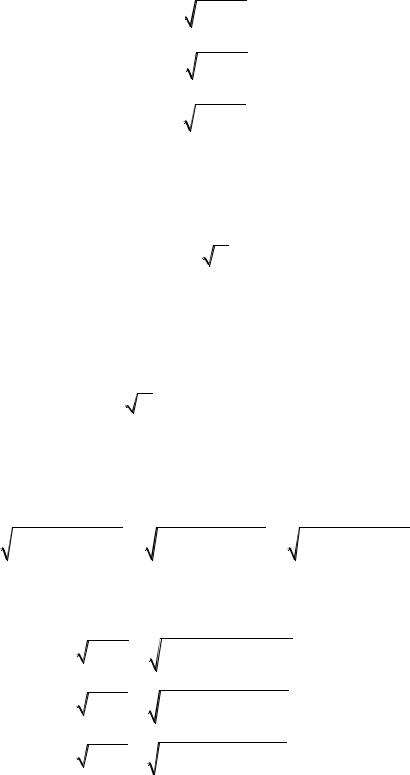
xy yz zx 2 3xyz x y z
xy 2 2xy2 z yz 2 2 xy yz zx zx 2 3x2 yz 3xy2 z 3xyz2
x2 y2 y2 z2 z2 x2 xyz x y z |
(1) |
Koshi teńsizliginen paydalanıp tómendegi teńliklerdi dúzemiz.
x2 y2 x2 z2 |
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
x4 y2 z2 |
x2 yz |
x2 yz, |
||||
2 |
|||||||||
|
|
|
|
|
|
|
|
||
y2 z2 x2 y2 |
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
x2 y4 z2 |
xy2 z |
xy2 z, |
||||
2 |
|
||||||||
|
|
|
|
|
|
|
|
||
z2 x2 z2 y2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
x2 y2 z4 |
xyz2 |
xyz2 |
||||
2 |
|
||||||||
|
|
|
|
|
|
|
|
||
Aqırǵı úsh teńsizlikti qossaq, (1) teńsizlik kelip shıǵadı. Teńsizlik dálillendi.
|
|
|
|
|
|
n 1 n |
|||
8-mısal. n natural sanlar ushın n! |
2 |
|
|
teńsizliktı dálilleń. |
|||||
|
|
|
|
|
|
|
|
|
|
|
n 1 n |
|
|
n 1 |
|
|
|||
|
|
|
|
||||||
Sheshılıwı: n! |
|
|
n n! |
|
|
|
(1) |
||
|
|
|
|||||||
|
2 |
|
|
|
|
2 |
|
|
|
n N san bolǵanlıqtan sonǵı teńsizlikti tómendegishe túrlendiremiz.
n 1 |
|
1 |
|
n 1 n |
|
1 |
1 2 3 ... n |
|
2 |
|
n |
2 |
n |
||||
|
|
|
|
|
||||
Bul teńliktı teńsizliktıń oń jaǵı menen almastıramız.
|
|
|
|
|
|
|
|
|
|
1 |
1 2 3 ... n |
|
|
|
|
|
||||||
|
|
|
|
|
n n! |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Nátiyjede orta arifmetikalıq hám orta |
geometriyalıq mánisler arasındaǵı |
|||||||||||||||||||||
qatnasqa tiykarlanıp (1) teńsizlik |
n 2 sanları ushın dálillendi. |
|
|
|
|
|||||||||||||||||
9-mısal. Oń a,b,c sanları ushın abc 8 shárt qanaatlandırılsa, onda |
||||||||||||||||||||||
|
|
a2 |
|
|
|
|
|
|
b2 |
|
|
|
|
|
c2 |
|
|
|
4 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 a3 |
1 b3 |
|
|
|
|
|
1 b3 |
1 c3 |
|
|
|
|
1 c3 |
1 a3 |
3 |
|
||||
Teńsizlikti dálilleń.
Sheshılıwı: Orta arifmetikalıq hám orta geometriyalıq mánisler boyınsha Koshi teńsizliginen paydalanıp,
|
|
|
|
|
|
|
|
|
|
|
2 a2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 a3 |
1 a 1 a2 a |
|
, |
||||||||||||
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 b2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 b3 |
1 b 1 b2 b |
|
, |
||||||||||||
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 c2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
1 c3 |
1 c |
1 c2 c |
|
|
|||||||||||
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Qatnaslardı alamız. Endi tómendegi teńsizliktı dálillesek jetkilikli boladı:
17
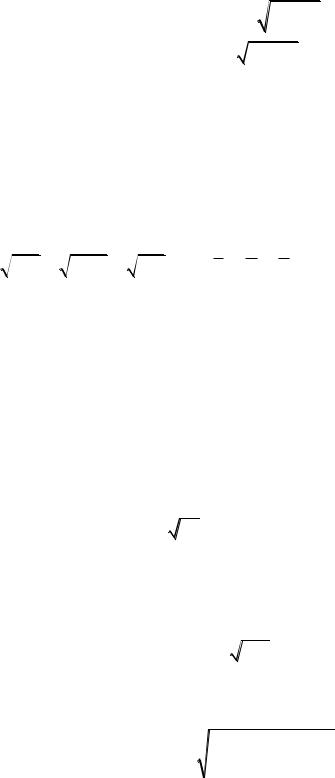
4a2 |
|
4b2 |
|
4c2 |
4 |
|
|
|
|
|
|
|
|
|
|
2 a2 2 b2 |
2 b2 2 c2 |
2 c2 2 a2 |
3 |
||||
3 a2 2 c2 b2 2 a2 c2 2 b2 2 a2 2 b2 2 c2
a2b2 b2c2 c2a2 2 a2 b2 c2 a2b2c2 8 72
Bul teńsizlik tómendegi teńsizliklerdi aǵzama-aǵza qosiwdan kelip shıǵadı.
a2b2 b2c2 c2a2 33 |
abc 4 48, |
2 a2 b2 c2 6 3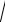 a2b2c2 24
a2b2c2 24
Demek joqarıdaǵılardan teńsizliktıń dálilleniwi payda boldı. Teńsizlik dálillendi. 10-mısal. Eger 0 a b c shárt orınlansa, onda tómendegi teńsizlikti
dálilleń.
a 3b b 4c c 2a 60abc
Sheshılıwı: Orta arifmetikalıq hám orta geometriyalıq mánisler boyınsha
berilgen Koshi teńsizliginen tómendegishe paydalanamız:
a 3b b 4c c 2a a b b b b c c c c c 2a
11
4 4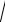 ab3 55
ab3 55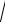 b c4 33
b c4 33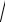 a2c 60a12 b20 c15
a2c 60a12 b20 c15
|
|
2 |
|
|
|
|
|
1 |
|
1 |
|
|
|||||
60abc |
|
c15 |
|
|
|
60abc |
c12 |
|
c |
20 |
|
|
|||||
1 |
|
|
1 |
|
1 |
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
a |
12 |
b |
20 |
|
|
a |
12 |
b |
20 |
|
||||||
|
1 |
|
|
|
1 |
|
||
c |
|
c |
|
|
||||
12 |
20 |
|
||||||
60abc |
|
|
|
|
|
|
60abc |
|
|
|
|
||||||
a |
b |
|
|
|||||
|
c c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Bunda |
|
, |
|
|
1 boladı. Teńsizlik dálillendi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Shınıǵıwlar. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1. Eger a,b,c R hám a2 |
b2 c2 |
1 bolsa, onda tómendegi teńsizliktı dálilleń. |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bc |
|
|
|
|
|
|
ac |
|
|
|
ab |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a a3 |
|
|
|
|
|
b |
b3 |
|
c |
c3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2. Eger a 0,b 0 bolsa |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizlikti dálilleń. |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|||||
3. |
Eger a ,a ,a ,a ,a 0 |
bolsa |
|
|
|
a2 |
a2 a2 |
a2 |
a2 |
a |
a a |
a |
||||||||||||||||||||||||||||||||||||
|
|
1 |
2 |
3 |
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
4 |
5 |
1 |
2 |
3 |
4 |
5 |
|
||||||||||||
teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4. Eger a 0,b 0,c 0 bolsa |
a b c |
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
abc teńsizlikti dálilleń. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. Eger a 0,b 0,c 0 bolsa |
|
a |
|
b |
|
|
c |
3 teńsizlikti dálilleń. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
c |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6. Teńsizliktı dálilleń. |
a b c d |
|
|
|
|
|
a2 b2 c2 d 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
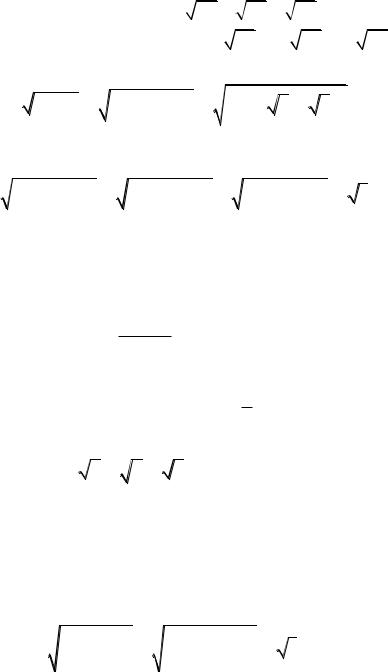
7. Eger a 0,b 0,c 0 bolsa, onda tómendegi teńsizliktı dálilleń.
a2 ab |
|
b2 bc |
|
c2 ac |
0 |
|
a b |
b c |
a c |
||||
|
|
|
8.Eger a 0,b 0,c 0 bolsa, a b c 
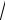 ab
ab 
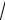 bc
bc 
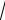 ac teńsizliktı dálilleń.
ac teńsizliktı dálilleń.
9.Eger a 0,b 0,c 0 bolsa, a3 b3 c3 a2 
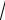 bc b2
bc b2 
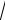 ac c2
ac c2 
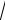 ab
ab
10. Eger a 0,b 0 sanları bar bolsa,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
c x 2 b c2 |
|||||||||||||||||||||
|
|
|
x2 a |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
a |
b |
||||||||||||||||||||||
teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11. Eger a,b,c 0 |
hám a b c 1onda tómendegi teńsizlikti dálilleń. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
a b c 2 b a c 2 c a b 2 |
|
|
|||||||||||||||||||||||||
|
|
3 |
|||||||||||||||||||||||||||
12. Eger a,b,c 0 |
hám a2 b2 |
c2 |
1 onda tómendegi teńsizlikti dálilleń. |
||||||||||||||||||||||||||
|
|
|
|
|
|
bc |
|
|
|
ac |
|
|
|
ab |
|
|
5 |
|
|||||||||||
|
|
|
|
|
a a3 |
|
b |
b3 |
|
c c3 |
2 |
|
|
|
|
|
|
|
|||||||||||
13. Eger a 0 bolsa, onda tómendegi teńsizlikti dálilleń.
a3 b3 3ab2 4 2
14. Eger a,b,c R bolsa, onda tómendegi teńsizlikti dálilleń.
a b 4 b c 4 a c 4 74 a4 b4 c4
15. Eger x, y, z 0 hám |
x y z 3 bolsa, onda tómendegi teńsizlikti dálilleń. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
y z xy xz yz |
||||||||||||||||||||||||
16. Eger a 0,b 0,c 0 bolsa, onda tómendegi teńsizlikti dálilleń. |
||||||||||||||||||||||||||||||||
a3 b3 c3 15abc 2 a b c a2 |
|
b2 c2 |
||||||||||||||||||||||||||||||
|
|
|
a2 |
|
|
|
b2 |
|
c2 |
|
|
|
ab bc ac |
|||||||||||||||||||
17. Eger a,b,c 0 bolsa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
7 dálilleń. |
|||||||
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
2 |
b |
2 |
c |
2 |
||||||||||||||||
|
|
|
b |
|
|
|
|
c |
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
||||||||
18. Eger a,b,c 0 bolsa, onda tómendegi teńsizlikti dálilleń. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
a |
|
b |
|
c |
|
|
|
|
ab bc ac |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
3 1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a2 b2 c2 |
|
||||||||||||||||||||||
|
|
b c a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
19. Egerde n natural san bolsa, tómendegi teńsizlikti dálilleń.
n 1 n 2n !!
20. Egerde n natural san bolsa, tómendegi teńsizlikti dálilleń.
n! |
2 |
|
n 1 2n 1 n |
|
|
|
|
|
|
|
6 |
|||
|
|
|
|
|
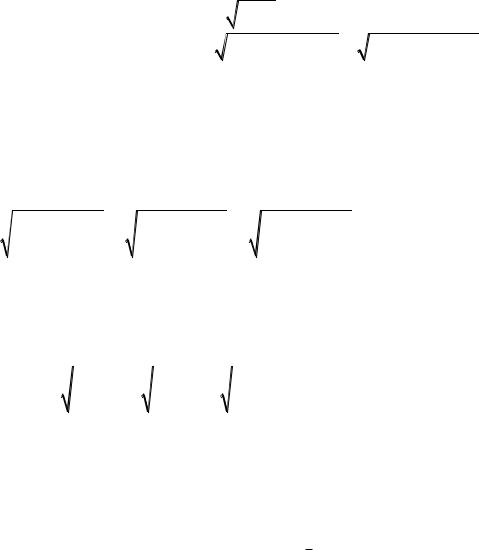
21. Egerde n natural san bolsa, tómendegi teńsizlikti dálilleń.
19
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n 3n 1 2 4 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n ! |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
22. Eger x, y, z 0 hám x y z 2 bolsa, |
|
|
|
x3 y y3 z z3 x |
|
xy3 yz3 zx3 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ni dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
23. Eger a,b,c 0 bolsa, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a b |
|
b c |
|
a c |
4 |
|
|
|
a |
|
|
|
|
b |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni dálilleń. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
b |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
c |
|
a |
|
|
b |
|
|
|
b c |
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
24. Oń a,b,c sanlardıń kóbeymesi birge teń bolsa, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1, 2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
a |
|
0,64 |
|
|
|
|
|
b |
|
0,64 |
|
c |
|
0,64 |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||
teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
25. Oń |
a,b sanlar ushın |
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
64 |
|
|
teńsizlikti dálilleń. |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 a b 3 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
|
3ab2 |
|
|
|
|
|
|
3a2b b3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
26. Oń a,b,c sanlar ab bc ca 1 teńlikti qanaatlandirsa, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
6b 3 |
1 |
|
6c 3 |
1 |
6a |
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
abc |
|
|
|
|
|
|
||||||||||
teńsizlikti dálilleń.
27. Eger x 0 hám n-oń putin san bolsa, onda tómendegi teńsizliktı dálilleń.
xn |
|
1 |
1 x x2 ... x2n |
2n 1 |
28. Eger a, b sanları oń hám hár qiyli sanlar bolsa, onda tómendegi teńsizliktı
n
dálilleń. an an1b an2b2 ... abn1 bn n 1 ab 2
29. Eger a 0, b 0, 0 p 1 sanları ushın tómendegi teńsizlikti dálilleń.
a b p a1 p a pb
30.Haqiyqiy oń x, y, z sanlar ushın shártdi xyz 1qanaatlandirilsa tómendegi
teńsizlikti dálilleń. |
x5 |
|
y2 |
|
z5 |
1 |
x5 y2 z2 |
y5 z2 x2 |
z5 x2 y2 |
3-§. Teńsizliklerdi dálillewde Matematikalıq indukciya metodınan paydalanıw
Matematikalıq induktsiya metodı teoremalardı, tastıyıqlawlardı hám teńsizliklerdı dálillewde keń túrde paydalanıladı.
İnduktsiya - «alıp keledi» degendi ańlatıwshı latın sózi.
Oqıwshı dáslepki waqıtlarda matematikalıq túsiniklerdi baqlaw, tájiriybe arqalı qabıl etiwge beyimlengen boladı; tájriybe hám baqlaw arqalı matematikalıq shınlıqtı úyreniw induktsiya dep ataladı. Ulıwma túrde induktsiya
20

dep dara tastıyıqlawlardan ulıwma tastıyıqlawlardı keltirip shıǵarıwǵa aytıladı. İnduktsiya tolıq, tolıq emes hám matematikalıq induksiya bolıp bólinedi.
Eger múmkin bolǵan dara jaǵdaylardıń birewinde qaldırmay qaraǵannan ulıwma juwmaq shıǵarılsa bul tolıq induktsiya boladı. Mısalı: ekinshi onlıqtaǵı ápiwayı sanlardı anıqlaw ushın ondaǵı barlıq sanlardı tómendegishe jazıwǵa boladı:
11 |
1 11; 12 |
1 |
2 |
2 |
3; 13 |
1 13; 14 |
1 |
2 |
7; 15 |
1 3 |
5; |
||||
16 |
1 |
2 |
2 |
2 |
2; 17 |
|
1 17; |
|
|
|
|
|
|
|
|
18 |
1 |
2 |
3 |
3; 19 |
1 19; 20 |
1 2 |
2 |
5 |
|
|
|
|
|||
Ekinshi onlıqta barlıǵı 4 ápiwayı san bar eken.
Egerde ulıwma juwmaq dara jaǵdaylardı tolıq qaramastan shıǵarılǵan bolsa, onda tolıq emes induktsiya boladı. Tolıq emes induktsiya tiykarında shıǵarılǵan juwmaqtıń durıslıǵına iseniwge bolmaydı.
Mısalı. у х2 х 41 úsh aǵzalıǵı mánislerinde ápiwayı san,
al x=40 mánisinde 412 quramalı san boladı.Solay etip biziń pikirimiz bir neshe dara jaǵdaylarda durıs bolıp, ulıwma alǵanda durıs bolmay shıqtı.
Endi soraw tuwıladı: bazı bir tastıyıqlawlar bir neshe dara jaǵdaylar ushın durıs, biraq barlıq dara jaǵdaylardı qarap shıǵıw múmkin emes, sonda bul tastıyıqlawdıń durıslıǵın qalay biliwge boladı. Bul soraw matematikalıq induktsiya metodı járdemi menen sheshiledi.
Matematikalıq induktsiya metodı
Matematikalıq induktsiya metodınıń tiykarı tómendegi printsipke tiykarlanǵan: Eger bazıbir tastıyıqlaw
1) n |
1 bolǵanda durıs hám |
|
2) usı tastıyıqlawdıń qanday da bir erikli n |
k mánisinde durıslıǵınan |
|
n k 1 |
bolǵanda da durıs bolatuǵınlıǵı kelip |
shıqsa, onda ol tastıyıqlaw |
qálegen natural n sanı ushın durıs boladı. Usı printsipke tiykarlanǵan dálillew metodı matematikalıq induktsiya metodı dep ataladı.
Endi biz Matematikalıq induksiya metodı járdeminde teńsizliklerdi dálillewdı úyrenemiz.
1-mısal: Eger n |
1 |
bolǵanda |
1 |
|
|
|
|
|
|
1 |
|
|
... |
|
1 |
|
13 |
|
teńsizlikti |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
n 1 |
|
|
|
n |
2 |
2n |
24 |
||||||||||||||||||||||||||
dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sheshılıwı: 1) Joqarıdaǵı tastıyıqlaw boyınsha dáslep |
n |
2 bolǵanda |
||||||||||||||||||||||||||||||||
mánisi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
1 |
|
|
7 |
|
|
14 |
13 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
1 |
2 |
2 |
3 |
4 |
|
12 |
|
24 |
24 |
|
|
|
|
|
|
|
|||||||||||||||
Teńsizlik orınlanadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) n k 1da |
|
1 |
|
|
|
1 |
|
|
... |
|
1 |
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k |
|
1 |
|
k |
2 |
|
|
2k |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
