
Tensizliklerdi dalillew usillari
.pdfTEŃSIZLIKLERDI DÁLILLEW
USÍLLARÍ
(Oqıw-metodikalıq qollanba)
Nókis-2019
1
Dúziwshiler: N.Djumabaev, M.Urazbaeva, E.Oteniyazov
Bul oqıw -metodikalıq qollanba joqarı oqıw orınlarınıń matematika fakulteti talabaları, akademiyalıq licey, kásip-óner kolledjleri, ulıwma bilim beriw mektepleri hám matematika páni tereńnen oqıtılatuǵın qánigelestirilgen mektep oqıwshıları hám oqıtıwshılar ushın «Teńsizliklerdi dálillew usılları» temasında jazılǵan bolıp, bul metodikalıq qollanbada teńsizliklerdi dálillewde oqıwshılardıń ózlestiriwi kerek bolǵan mısallar bir neshe usıllar menen dálillenip kórsetilgen.
2

1-§. Teńsizlikler dálillew boyınsha tusınık
1.1 Teńsizlikler boyınsha ulıwma túsinik
Meyli f x g x yamasa f x g x teńsizligi berilgen bolsın. Berilgen
teńsizlikti durıs sanlı teńsizlikke aylandıratuǵın ondaǵı ózgeriwshilerdiń hár qanday mánisleri teńsizliktiń sheshimleri dep ataladı. Ózgeriwshisi bar teńsizlikti sheshiw degenimiz, bul demek, onıń barlıq sheshimlerin tabıw yamasa olardıń joq ekenligin dálillew degen sóz.
Bir ózgeriwshige iye bolǵan eki teńsizliktiń sheshimleri duspa-dus kelse, onda olar teń kúshli teńsizlikler dep ataladı: dara jaǵdayda eki teńsizliktiń ekewi de sheshimlerge iye bolmasa, onda olar da teń kúshli teńsizlikler boladı.
Teńsizliklerdi sheshiw waqtında ádette berilgen teńsizliklerdi ádewir
ápiwayıraq biraq berilgen teńsizlikke teń kúshli bolǵan teńsizlikler menen almastıradı; kelip shıqqan teńsizlikti taǵı da ádewir ápiwayıraq biraqta berilgen teń kúshli bolǵan teńsizlikler menen almastıradı hám t. b. Bunday almastırıwlar mına tómendegi tasqıyıqlawlarǵa tiykarlanıp ámelge asırıladı.
1. Eger teńsizliktiń bir jaǵındaǵı qosılıwshını qarama-qarsı belgisi menen
f x |
h x |
g |
x |
h x ekinshi |
jaǵına kóshirsek, onda berilgenge |
teń |
|
kúshli bolǵan teń |
6x |
12 sizlik kelip shıǵadı. Eger h x ańlatpa |
x X larda |
||||
aniqlanǵan bolsa, |
f x g x hám |
teńsizlikler teń kúshli. Mısalı x2 5x |
6 |
||||
hám x2 |
5x |
6 |
0 teńsizlikleri. |
|
|
|
|
2. Eger bir ózgeriwshige iye bolǵan teńsizliklerdiń eki jaǵın da birdey oń sanǵa kobeytsek yamasa bólsek, onda berilgen teńsizlikke teń kúshli bolǵan teńsizlik kelip shıǵadı. Mısalı 3x2 6x 9 hám x2 2x 3 0 teńsizlikleri.
3. Eger bir ózgeriwshige iye bolǵan teńsizliklerdiń eki jaǵın da birdey teris sanǵa kóbeytsek yamasa bólıp, sonıń menen bunda teńsizlik belgisin qaramaqarsı belgige ózgertsek, onda berilgen teńsizlikke teń kúshli bolǵan teńsizlik kelip shıǵadı. Mısalı hám x 2 teńsizlikleri.
2 hám 3-lerge tıykarlanǵan halda tómendegi tastıyıqlawdı keltırıp ótsekte boladı.
4. Eger teńsizliktiń eki jaǵin da ózgeriwshilerdiń barliq mánislerinde oń mániske iye bolatuǵn qanday da bir ańlatpaǵa kóbeytsek yamasa bólsek, onda
berilgen teńsizlikke teń kúshli bolǵan teńsizlik kelip shıǵadı. Mısalı Eger hámme |
||||
x X larda |
h x 0 bolsa, |
f x g x |
hám |
f x h x g x h x |
teńsizlikler teń kúshli boladı.
5. Eger teńsizliktiń eki jaǵın da ózgeriwshilerdiń barlıq mánislerinde teris mániske iye bolatuǵın qanday da bir ańlatpaǵa kóbeytsek yamasa bólıp, sonıń menen bunda teńsizlik belgisin qarama-qarsı belgige ózgertsek, onda berilgen
teńsizlikke teń kúshli bolǵan teńsizlik kelip shıǵadı. Mısalı Eger hámme x X
larda h x 0 bolsa, f x |
g x hám f x h x g x h x teńsizlikler teń |
|
4 |

kúshli boladı. Demek teńsizliklerdı sheshıwde joqarıdaǵı tastıyıqlawlardan paydalansaq teńsizliktıń anıq sheshımlerin tapqan bolamız.
1.2 Sanlı teńsizliklerdı dálillew
Sanlı teńsizliklerdı dálillewde tómendegishe qásiyetlerdı keltırıp ótemiz hám usılar boyınsha dálilleymız.
Qálegen a hám b sanlar ushın tómendegi úsh qatnasdan tek ǵana birewi orınlı:
1.a b 0, a b
2.a b 0, a b
3.a b 0, a b.
|
|
|
|
Sanlı teńsizlikler tómendegishe qásiyetlerge iye: |
|
|
|
||||||||||||||||||||||||||||||||||||
- |
Eger a |
|
b hám b |
c bolsa onda a c ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
- |
Eger a |
|
b bolsa onda a |
|
|
m |
b |
m ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
- |
Eger |
a1 |
|
b1,a2 |
|
b2,...,an |
|
bn, bolsa a1 |
a2 |
|
|
|
|
... |
an |
|
b1 |
b2 |
... |
bn |
|||||||||||||||||||||||
|
orınlı |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- |
Eger |
a |
|
b |
bolsa, |
|
m |
0 |
|
ushın |
sanı |
am |
|
|
bm, |
m |
0 sanı ushın |
am bm |
|||||||||||||||||||||||||
|
teńsizlikleri orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
- |
Eger a1 |
|
b1 |
|
0, a2 |
|
|
b2 |
|
|
|
0, ..., an |
bn |
|
|
0 bolsa a1a2...an |
b1b2...bn orınlı |
||||||||||||||||||||||||||
- |
Eger a |
|
b |
0 bolsa ax |
|
bx orınlı. bunda x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
- |
Eger a |
|
1 hám x |
|
|
y |
0 bolsa, onda ax |
|
|
|
ay , 0 |
|
|
a |
|
1 hám x |
y |
0 bolsa |
|||||||||||||||||||||||||
|
ax |
ay |
teńsizlikleri orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Teńsizliklerde dálillewde qollanılatuǵın usıllardıń bırı bul ayırmanıń |
|||||||||||||||||||||||||||||||||||||||
|
belgisin baxalaw usılı. Bul usıldıń maǵanası tómendegilerden ibarat boladı: |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x; y; z) g x; y; z |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Teńsizlikleriniń |
durıslıǵın |
|
|
anıqlaw |
|
|
|
ushın, |
|
|
olardıń |
ayırmasın, |
||||||||||||||||||||||||||||||
|
f (x; y; z) g (x; y; z) |
|
ti |
duzedi |
hám |
|
bul ayırmanıń |
oń |
bolatuginlıǵın |
||||||||||||||||||||||||||||||||||
|
dálilleydi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1-Mısal. Eger x 0, y 0 |
bolsa , onda x y |
|
|
|
|
|
bolatuǵinlıǵın dálilleniz. |
|||||||||||||||||||||||||||||||||||
|
|
xy |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sheshiliwi. Bulardıń ayırmasın duzemiz: x y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
xy 0 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Bunnan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|
|
x y 2 |
|
xy |
|
( |
x y )2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
teńsizligi, x |
|
penen y tiń teris emes qálegen mánislerinde, durıs |
||||||||||||||||||||||||||||||||||
|
( x |
y )2 0 |
|
||||||||||||||||||||||||||||||||||||||||
|
boladı. Demek , x y |
|
|
|
|
, sonıń menen bunda tek ǵana x y bolgan jágdayda |
|||||||||||||||||||||||||||||||||||||
|
xy |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ǵana teńlik kelip shıǵadı.
5

2-mısal. |
a2 |
b2 2 |
4ab a b 2 teńsizlikti dálilleń. |
||||
Sheshılıwı: Berilgen teńsizlikti tómendegishe jazamız. |
|||||||
|
|
|
|
a b 2 a b 2 |
4ab a b 2 |
||
Eger a |
b bolsa, onda teńlik kelip shıǵadı. Eger a b bolsa, onda a b 2 0 |
||||||
bolǵanlıqtan, teńsizliktıń eki jaǵın |
a |
b 2 qa bólemız. |
|||||
Nátiyjede |
|
a |
b 2 |
4ab |
|||
teń kushli |
|
|
|
|
|
|
|
|
|
|
a2 |
2ab b2 |
4ab , a2 2ab b2 0 |
||
Bunnan |
a |
b 2 |
0 kelip shiǵadı. Teńsizlik dálillendi. |
||||
3-mısal. |
ab |
bc |
ca 2 |
3abc(a |
b |
c) teńsizlikti dálilleń. |
|
Sheshılıwı: Teńsizlikti dálillew ushın teńsizliktıń oń jaǵın shep jaǵına ótkeremiz.
a2b2 |
b2c2 |
|
c2a2 |
|
|
2a2bc |
|
|
2ab2c |
|
|
2abc2 |
|
|
|
3a2bc |
3ab2c |
|
|
3abc2 0 |
||||||||||||||||||||||||||||||||||||||||||||
yamasa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2a2b2 |
|
|
|
|
2b2c2 |
|
2c2a2 |
|
2a2bc |
2ab2c |
|
2abc2 |
0 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a2 b2 |
|
|
2bc c2 |
|
b2 a2 |
|
|
|
2ac c2 |
|
|
|
|
|
c2 a2 |
|
2ab b2 |
0 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
a b |
c |
2 |
|
|
|
b a |
|
|
c |
2 |
|
|
|
|
c |
|
a |
b |
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Teńsizlik a,b,c |
sanları ushın orınlı. Eger |
a b c |
bolsa teńlik belgisi kelıp |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
shúıǵadı. Teńsizlik dálillendi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
4-mısal. Eger x |
|
|
|
|
|
|
|
0 sanları ushın |
|
|
x |
|
y |
24 |
|
|
|
|
|
teńsizligin dálilleń. |
||||||||||||||||||||||||||||||||||||||||||||
0, y |
|
|
|
|
|
|
xy |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
y |
|
|
|
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Sheshılıwı: teńsizlikti tómendegishe turlendiremiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
x |
|
y |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
24 |
|
xy |
|
|
|
|
|
|
|
24 |
|
xy |
|
|
|
|
|
24 xy |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
y |
|
|
x |
|
|
4 |
|
y |
|
|
|
|
4 |
|
x |
|
|
|
|
|
4 y |
|
|
4 x |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Nátiyjede |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
x |
|
|
y |
|
24 |
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
xy |
|
|
|
|
|
|
0 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
y |
x |
|
|
|
|
4 y |
4 |
x |
|
|
|
|
|
|
4 |
|
y 4 |
x |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
teń belgisi tek ǵana x |
|
|
y de, x, y qalǵan mánıslerinde teńsizlik orınlanadı. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5-mısal. a2 4b2 |
3c2 |
14 2a 12b 6c teńsizlikti dálilleń. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sheshılıwı: a2 4b2 |
3c2 |
14 2a 12b 6c 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
a2 2a 1 4b2 12b 9 3c2 6c 3 1 a 1 2 2b 3 2 3 c 1 2 1
a 1 2 2b 3 2 3 c 1 2 1 0
sonǵı teńlik a,b,c qálegen mánısınde teńsizlik orınlı ekenin dálilleydi.
6

6-mısal. |
Eger |
|
1 |
|
1 |
|
2 |
|
|
hám ac |
0 |
|
|
a |
|
b |
|
|
|
|
|
|
c |
b |
|
4 bolsa, teńsizliginıń |
|||||||||||||||||||||||||||
|
a |
|
|
|
c |
|
|
b |
|
|
2a |
|
|
b |
|
|
|
|
|
2c |
b |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
orınlı ekenın dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Sheshılıwı: |
1 |
|
1 |
|
2 |
teńliginen b nı tawıp, berilgen teńsizlikke aparıp qoyamız. |
|||||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
c |
|
|
|
b |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
2ac |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
2ac |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
a a c |
|
|
2ac |
|
|
|
a 3c |
|
||||||||||||||||||||||||||||
|
|
|
|
|
a c |
|
|
|
|
|
|
(1) |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
2a b |
2a |
|
|
|
2ac |
|
2a a c |
|
|
|
|
2ac |
|
|
|
|
2a |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
2ac |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
c b |
|
|
|
|
|
|
|
|
|
|
|
|
c a c |
|
|
|
|
|
|
2ac |
|
|
3a c |
|
|
||||||||||||||||||||||||
|
|
|
|
a c |
|
|
|
|
|
|
|
|
|
(2) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
2c b |
2c |
|
|
|
2ac |
|
2c a c |
|
|
2ac |
|
|
|
|
2c |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(1) hám (2) lerdi qosamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
|
c b |
|
|
|
a 3c 3a c |
, |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
b |
|
2c |
|
b |
|
|
|
2a |
|
|
|
|
|
|
|
|
2c |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
c b |
|
|
2ac 3 a2 |
c2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
b |
2c |
|
b |
|
|
|
|
|
|
|
|
|
2ac |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
c |
b |
|
1 |
3 |
|
a |
|
|
|
c |
|
|
|
|
4, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
b |
2c |
|
b |
|
2 |
|
|
|
c |
|
|
|
a |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Sebebi |
ac |
0 . |
|
Teńlikke |
|
|
tek |
|
|
ǵana a |
|
b |
|
|
c |
|
|
bolǵanda |
erisemiz. Teńsizlik |
||||||||||||||||||||||||||||||||||
dálillendi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7-mısal. Eger a b c 0 bolsa a3 |
|
b3 |
|
c3 3abc teńsizligin dálilleń. |
|||||||||||||||||||||||||||||||||||||||||||||||||
Sheshılıwı: a3 b3 |
c3 |
3abc ańlatpasın a3 |
b3 |
ǵa keltiremiz. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
a3 b3 c3 3abc a3 3a2b 3ab2 |
b3 c3 3ab2 |
3abc |
||||||||||||||||||||||||||||||||||||||||||||||||||
a b 3 3ab a b c c3
a b 3 c3 kublardıń qosındısı boyınsha jayamız.
7

a b 3 c3 3ab a b c a b c
a b 2 a b c c2 3ab a b c
a b c a2 2ab b2 ac bc c2 3ab
a b c a2 b2 c2 ab bc ac
12 a b c 2a2 2b2 2c2 2ab 2bc 2ac
12 a b c a b 2 a c 2 b c 2 .
Sonǵı teńlik |
|
a b c 0 boyınsha teris emes. Eger a b c bolsa teńlik |
|||||||||
qanaatlandıradı. |
Demek bul teńlik a,b,c lar ushın teńsizliktıń orınlı bolıwın |
||||||||||
dálilleydi. |
|
|
|
|
|
|
|
|
|
|
|
8-mısal: S |
|
1 |
|
|
2 |
|
... |
n |
|
1 |
dálilleń. |
|
83 |
92 |
|
7 n 2 7 n 3 |
|
||||||
82 |
|
93 |
|
7 |
|
||||||
Sheshılıwı: ulıwma aǵzası ushın tómendegishe teńsizlikti keltireyik.
|
n |
|
n |
|
|
1 |
|
|
|
|
|
|
|
7 n 6 n |
|
1 |
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
7 n 2 7 n 3 |
7 n 3 |
|
7 n 2 |
7 n 6 n |
6 n |
7 n |
|||||||||||||||||||||
Nátiyjede |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
82 |
83 |
7 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
92 93 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
.................. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
7 n 2 7 n 3 |
|
|
|
6 n |
7 n |
|
|
|
|
|
|
||||||||||||||
Joqarıdaǵı teńsizliklerdi |
qossaq |
|
S |
|
1 |
|
|
|
|
|
1 |
|
|
1 |
kelip |
shıǵadı. |
Teńsizlik |
|||||||||||
|
7 |
|
|
|
7 n |
7 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
dálillendi.
9-mısal: a2 b2 a4 b4 a3 b3 2 teńsizlikti dálilleń. Sheshılıwı: teńsizliktiń eki jaǵın apiwayılastıramız.
a b 2 a b 2 a2 b2 a b 2 a2 ab b2 2
Eger a b bolsa teńlik orınlı. Eger a b bolsa, onda a b 2 0 bolǵanlıqtan
8
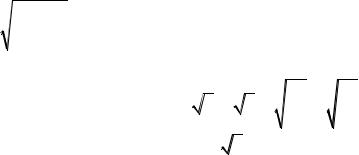
a b 2 a2 b2 a2 ab b2 2
teńsizligin dálillew qaladı. |
|
|
|
|
|
a2 b2 2ab a2 b2 a2 b2 ab 2 |
|
|
|||
a2 b2 2 2ab a2 b2 a2 b2 2 a2b2 2ab a2 b2 |
|
||||
a2b2 0, a,b nıń qálegen mánisinde orınlı. Teńsizlik dálillendi. |
|
||||
10-mısal: |
a 0,b 0,c 0 |
hám |
p-qálegen |
sanları |
ushın |
a b c 0, a c b 0,b c a 0 |
|
teńsizlikleri |
orınlı |
bolsa |
|
pa2 1 p b2 |
pc2 0 teńsizligin dálilleń. |
|
|
||
Sheshılıwı: teńsizlikti kvadrat teńsizlik kórinisine alıp kelemiz. |
|
||||
|
pa2 1 p b2 pc2 |
c2 p2 a2 b2 c2 |
p b2 |
|
|
|
c2 p2 a2 b2 c2 p b2 |
0 |
(1) |
|
|
Teńsizlik qálegen p sanı ushın orınlı bolıwı kerek. с2 0 bolıp, teńsizlik orınlı bolıwı ushın p qarata berilgen kvadrat úsh aǵzalısınıń diskriminantı teris mániske iye bolıwı kerek.
Da2 b2 c2 2 4b2c2 a2 b2 c2 2bc a2 b2 c2 2bc
a2 b c 2 a2 b c 2 a b c a b c a b c a b c
a b c a b c b c a c a b .
bizge berilgen
a b c 0, a c b 0, b c a 0
teńsizliktiń shártlerin esapqa alǵan halda sonǵı teńlikten
a b c a b c a c b b c a 0 . (2)
Nátiyjede (2) boyınsha D 0 bolıwı kelip shıǵadı. Bul (1) teńsizliktiń p nıń qálegen mánisinde teńsizliktı qanaatlandırıwın dálilleydi.
|
|
|
|
|
|
|
|
|
|
|
Shınıǵıwlar |
|
|
|
|
|
|
|||||||
1. |
|
|
a2 |
|
1 |
teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
a4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a b |
|
|
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
|
|
|
|
|
|
|
|
teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. 1 2a4 a2 |
2a3 teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
b2 |
|
|
4. Eger |
a 0, b 0, sanları ushın |
|
a |
|
b |
|
|
|
teńsizligin dálilleń. |
|||||||||||||||
|
b |
a |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Eger a 0 sanı ushın a3 2 a2 |
2 |
|
|
|||||||||||||||||||||
a teńsizligin dálilleń. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
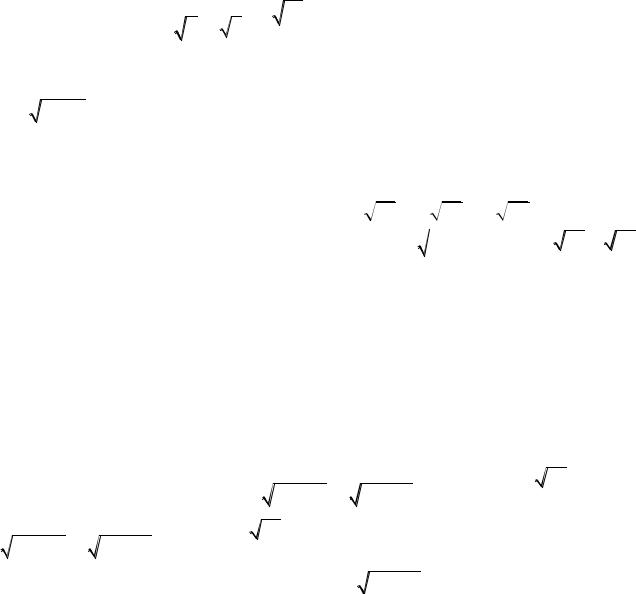
6. Eger a 0,b 0, ay bx 0 |
hám |
x y |
bolsa |
a b xy |
|
ax by |
teńsizliginıń |
||||||||||||||||||||||||||||||||||||
|
ay bx |
a b |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
orınlı bolıwın dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7. Eger a 2 bolsa |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
teńsizligin dálilleń. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
a2 |
4a 4 |
a3 |
|
8 |
|
||||||||||||||||||||||||||||||||||||||
8. Eger |
a 0,b 0,c 0, |
bolsa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
6abc ab a b bc b c ca c a 2 |
a3 b3 c3 teńsizligin dálilleń. |
||||||||||||||||||||||||||||||||||||||||||
9. Eger a 1 bolsa a3 1 a2 |
a teńsizlikti dálilleń. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
abc 0 bolsa |
1 |
|
1 |
|
|
|
1 |
|
|
|
a8 b8 c8 |
|
|
|
|||||||||||||||||||||||
10. Eger |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizliginıń orınlı bolıwın |
|||||||||||||||||||||||
|
|
a |
|
b |
|
c |
|
|
a3b3c3 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x 0, y 0, |
|
x |
|
|
|
y |
|
|
|
2 4 |
|
|
|
|||||||||||||||||||||||||||
11. Eger |
|
|
|
|
|
|
xy teńsizligin dálilleń. |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
12. Eger a 0, b 0 bolsa, onda a2 b2 c2 |
ab ac bc teńsizlikti dálilleń. |
||||||||||||||||||||||||||||||||||||||||||
13. |
a2 3 |
|
|
2 teńsizligin dálilleń. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
a2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
14. Eger |
|
a |
|
c |
, bolsa |
|
a b |
|
c d |
|
dálilleń. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
b |
|
|
|
d |
|
|
b |
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
15.Egerde c, d oń sanlar bolıp a c d,b c d , bolsa ab bc ad dálilleń.
16.a 0, b 0, c 0 sanları ushın a3 b3 c3 a2 
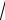 bc b2
bc b2 
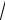 ac c2
ac c2 
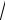 ab dálilleń.
ab dálilleń.
|
|
|
|
|
|
|
17. Egerde a, b, c, d teris emes sanları berılgen bolsa a c |
b d |
|
ab cd |
|||
dálilleń.
18.a2 b2 a4 b4 a3 b3 2 teńsizlikti dálilleń.
19.a b,b c,c 0 bolsa a b b c a c 8abc teńsizlikti dálilleń.
20.x4 y4 z2 1 2x xy2 x z 1 teńsizlikti dálilleń.
21.x12 x9 x4 x 1 0 teńsizlikti dálilleń.
22.Egerde zy yz zx 1 bolsa, x2 y2 z2 1 dálilleń.
23.2x4 1 2x3 x2 teńsizlikti dálilleń.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
x b |
|
|
|
|
|
|
|
||
24. |
a b 0 sanları |
|
ushın |
|
|
|
|
|
|
|
egerde |
x ab , |
hám |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
x2 a2 |
x2 b2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x a |
|
|
|
|
x b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
egerde x |
ab teńsizliklerdi dálilleń. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x2 a2 |
x2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
y2 |
1 |
|
|
|
|
|
x c 2 y2 |
4a2 |
||||||||||||||||||
25. Egerde |
|
a |
|
|
|
b |
|
, |
|
|
hám c |
|
a2 b2 bolsa |
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizliginıń orınlı ekenın dálilleń.
10
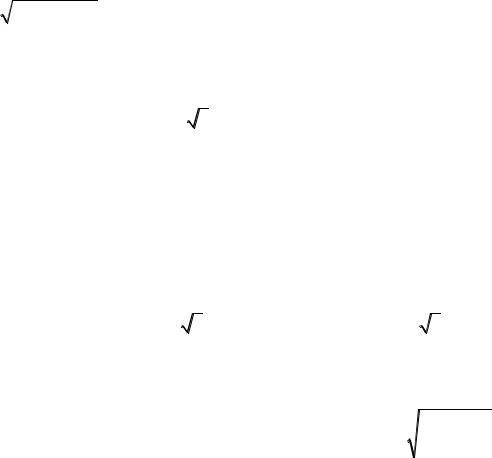
26. x tıń qálegen mánisinde teńsizliktiń orınlı bolıwın dálilleń.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x |
|
|
|
|
|
x 1 |
|
|
|
|
|
|
x 2 |
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
27. Eger a 0, b 0 sanları ushın |
1 a b |
|
1 a b ab |
teńsizlikti dálilleń. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 a b |
|
|
|
|
|
|
|
|||||||||||
28. |
|
Egerde a2 b2 |
|
|
1 hám c2 d 2 |
|
1 bolsa |
|
ac bd |
|
1 teńsizligin dálilleń. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
29. |
|
|
|
a2 b2 c2 |
|
|
|
a |
|
|
|
b |
|
|
|
c |
|
|
teńsizligin dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
30. |
|
1 |
|
|
1 |
... |
1 |
|
2n 1 |
teńsizlikti |
dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1! |
2! |
|
|
n! |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
31. |
|
P |
|
3 7 11... |
4n 1 |
|
|
1 |
|
|
teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
5 9 13... (4 n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
32. a,b,c- sanları ushmúyeshliktıń tárepleri uzınlıqları bolsa |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 b c a b2 (c a b) c2 a b c 3abc |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
teńsizliktı dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 !! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
33. |
|
S |
|
1 |
|
1 3 |
|
|
|
... |
1 Teńsizliktı dálilleń. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
32 |
2! |
|
|
3n |
|
n! |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 1! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
34. Eger x 0 sanı ushın |
x |
|
|
|
4x 4 |
2x 1 2x |
|
|
|
|
x2 1 |
0 teńsizlikti dálilleń. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t t3 2z |
|
3 |
|
|
t 1 t 1 3 2z |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
35. |
|
Eger t 0 |
|
hám t 3 |
|
z t 1 |
bolsa, |
|
|
|
z |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2t3 z |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t 1 3 z |
|||||||||
teńsizlikti dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
36. |
m, n natural sanları ushın tómendegi teńsizlikti dálilleń. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
4n 1 |
|
|
m 2n ! |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
|
|
m |
|
|
|
|
|
|
... m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
m! |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1.3 Teńsizliklerdi qarsıdan dálillew usılı menen dálillew.
Bul usıldiń maǵanası mına tómendegilerden ibarat boladı. Meyli mınaday teńsizliktiń shın ekenligin dálillew kerek bolsın deyik :
f (x; y; z) g(x; y; z) |
(1) |
Bunı kerisinshe uyǵarıp kóreyik, yágnıy ózgeriwshilerdiń qanday da bolmasın bir toparı ushın mına teńsizlik durıs boladı deyik:
f (x; y; z) g(x; y; z) |
(2) |
Tensizliklerdiń qásiyetlerin qolllanıp, (2) teńsizlikti turlendiriwdi orinlaydı. Egerde usı turlendiriwlerdiń nátiyjesinde nadurıs kelip shıqsa, onda bul
(2) teńsizliktiń durıslıgı haqqında boljawımız nadurıs bolıp shıǵadı, al sonıń ushın da (1) teńsizlik durıs boladı.
1-mısal. Eger a 0,b 0,c 0,d 0 bolsa mına teńsizlikti dálilleń:
11
