
Aniq integrallar
.pdf
3). Eger |
0 |
bolsa, |
0 sanına |
n N |
sanın sonday tańlaymız, |
||||||||||||||||||||||||||
|
2n teńsizligi orınlı bolsın. Onda |
|
2n |
|
|
, |
2n |
5 |
|||||||||||||||||||||||
nátiyjede |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
bolǵanda |
|
|
ushın |
|
cos x 1 |
|
hám |
|
x 1 mánislerinde |
|
1 |
1 |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
x |
|
, |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
teńsizliklerin esapqa alıp, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 2 n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
5 |
2 n |
cos x dx |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
cos x |
dx |
|
|
3 |
|
1 |
3 |
dx |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
teńsizliginıń orınlı bolıwın kóremiz. |
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Bul |
teńsizliktiń |
orınlı |
bolıwı |
|
|
|
|
dx |
|
funkciyası |
|
ushın |
menshiksiz |
||||||||||||||||||
|
x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
integrallardı jıynaqlılıǵına arnalǵan Koshi belgisi orınlı emes ekenligin kórsetedi.
Juwmaq: Berilgen qatar 1 bolsa jıynaqlı; 0;1 mánislerinde shártli
jıynaqlı; 0 mánislerinde tarqalıwshı boladı.
Menshiksiz integrallardı jıynaqlılıqqa izertlewde tómendegi tastıyıqlawdı
biliw paydalı boladı. |
|
|
|
|
|
Teorema. Eger g x |
funkciya a;b te absolyut integrallanıwshı bolsa, |
|
b |
|
b |
onda J1 f x dx |
hám J2 f x g x dx menshiksiz integralları yamasa |
|
a |
|
a |
birge jıynaqlı, yamasa birge tarqalıwshı, yamasa birge shártli jıynaqı boladı.
Yaǵnıy absolyut integrallanıwshı funkciyaǵa integral astında ekinshi bir funkciyanı qosıw yamasa alıw integraldıń jıynaqlılıǵına, absolyut hám shártli jıynaqlılıǵına tásirin tiygizbeydi.
§8. Menshiksiz integrallar jıynaqlılıǵınıń Abel hám Dirixle belgileri
Teorema: (Dirixle belgisi).Meyli a; kesindisinde |
f x úzliksiz, al |
g x úzliksiz differenciallanıwshı funkciya bolıp, |
|
x
1) F x f t dt funkciyası a; de shegaralanǵan, yaǵnıy
a
M 0 : x a; F x M .

|
|
2) |
g |
|
x |
|
|
|
funkciyası |
|
a; |
kesindisinde |
|
belgisin saqlaydı, yaǵnıy |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x a; ushın |
g x 0 |
|
|
|
yamasa |
|
|
|
g x 0 |
|
|
|
teńsizliklerinen tek |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
birewi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3) |
lim g |
x 0 . Onda |
|
J f x g x dx |
|
menshiksiz integralı jıynaqlı |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Dálillew: |
a |
|
hám |
|
a |
|
mánislerin |
|
|
alıp, |
bóleklep |
integrallaw |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
formulasınan paydalansaq, |
|
|
|
|
dv f x dx |
|
|
F |
|
|
x |
|
g |
|
|
x |
|
|
|
|
|
F |
|
|
x |
|
g |
|
|
x dx |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
f x g x dx |
u g x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
v F x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
teńligi kelip shıǵadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Onda 1) shártti esapqa alǵanda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
F x g x |
|
|
|
|
M |
|
|
|
|
g |
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F x g x dx M |
|
|
|
|
|
|
|
g x dx |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
teńsizlikleri orınlı boladı. Endi 2) shártten, eger |
|
g x 0 |
|
|
|
bolsa, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g x dx |
g x dx g g , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eger g x 0 |
|
|
bolsa, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g x dx |
|
g x dx g g . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Demek, bul eki jaǵday ushın da |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
g |
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g x dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizligi orınlı. Onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x g x dx |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3- shárttegi shektiń anıqlamasınan 0, |
|
|
a : x |
; |
|
g x |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4M |
|||||||
Demek, , ; |
mánisleri ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x g x dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4M |
|
|
4M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yaǵnıy |
f x g x dx funkciya ushın |
Koshi |
|
belgisindegi shártler |
orınlı. Bul |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
menshiksiz integralı jıynaqlı bolıwı ushın zárúr hám jeterli.
Dálillengen teoremanıń saldarı tómendegi Abel belgisin beredi.

|
|
f x funkciyası |
a, kesindisinde úzliksiz, |
|
x dx |
||||||
Saldar: Eger |
f |
||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
menshiksiz integral |
jıynaqlı, al |
g x |
funkciyası |
a; kesindisinde |
|||||||
shegaralanǵan bolıp, |
g x tuwındısı |
x monoton funkciya bolsa, onda |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f x g x dx |
menshiksiz integralı jıynaqlı boladı. |
|
|
|
|
|
|||||
a |
|
|
|
|
|
|
|
|
|
|
|
Haqıyqatında da monoton funkciyalardıń shegi haqqındaǵı teoremaǵa sáykes |
|||||||||||
g x qa qoyılǵan shártler orınlı bolǵanda |
lim g |
x g |
|
shekli shegi bar |
|||||||
|
g1 x g x g |
|
x |
|
|
g1 x |
|
|
|||
boladı. Onda |
belgilewin |
kiritsek, |
funkciyası |
||||||||
a; kesindisinde monoton nolge umtıladı. Onda Dirixle belgisine sáykes |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f x g1 x dx |
menshiksiz |
|
integralı |
|
jıynaqlı. |
Bunnan |
|||||
a |
|
|
|
|
|
|
|
|
|
|
|
f x g x f x g f x g1 x |
teńligi |
x a; |
orınlı |
bolǵanı |
ushın |
||||||
f x g x dx integralı da jıynaqlı degen juwmaqqa kelemiz.
a
Shınıǵıwlar |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. |
Shegaraları |
sheksiz |
menshiksiz integrallardı |
|
ji’ynaqlılıqqa tekseriń |
||||||||||||||||||||||||
1. |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
16. |
(x sin x)dx |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
0 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
x |
2 |
e |
xdx |
|
|
|
|
|
|
||||
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
|
|
dx |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
18. |
xex |
dx |
||||||||||||||||||
|
|
x ln x |
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
|
|
|
dx |
|
|
|
|
|
|
||||||
|
sin xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5. |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
(x 1)dx |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x2 |
1 |
|
|
|
|
|
20. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4x |
2 |
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
6. |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
dx |
21. |
|
|
|
|
|
dx |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
2 |
1 |
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
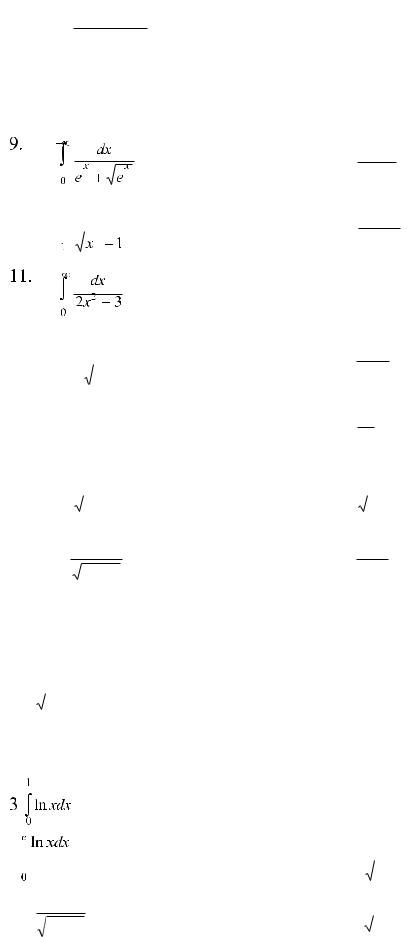
7. |
|
|
4dx |
|
|
|
|
||
|
|
|
||
|
|
x2 |
2x 2 |
|
|
|
|
|
|
8. |
|
5x |
|
|
|
|
|
|
|
|
e |
|
dx |
|
|
0 |
|
|
|
10. |
|
dx |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
12. |
0 |
arcsin xdx |
||
|
||||
|
|
|||
|
|
|
|
|
|
|
1 x2 |
||
13. 0
( e3x 2x)dx
14. |
|
dx |
|
|
|
|
|
|
|
|
|
|
x 1 |
||
|
0 |
|
|
|
|
|
|
15. xdx
2x 1
1
22. x 2ex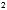 dx
dx
0
23. x3 sin 3xdx
3
1 dx
24.1 x2
xdx
25.0 x 2 4
3x
26. 3xe dx
0
dx
27. 1 x ln x
ex
28. dx
1 x
|
xdx |
|
29. |
|
|
|
|
|
|
|
|
x 5 |
||
|
|
|
x2dx
30. x 9
0
2. Shegaralanbag’an funktsiyalardan ali’ng’an menshiksiz integrallardi’ yesaplan’
1 |
|
|
|
xdx |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
16 |
x ln xdx |
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 x |
|
|
|
|
||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
dx |
|
ln 2 ex |
|
|
|
|||||||||||||
2 |
|
|
17 |
|
|
|
|
|
dx |
|
||||||||||||
x2 2x 3 |
|
|
|
x |
|
|
||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
dx |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
dx |
|
||||
4 |
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x |
2 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
2 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
x dx |
|
|
|
20 |
|
|
xdx |
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
x 1 |
|
||||||||||||
1 |
x |
|
1 |
|
|
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
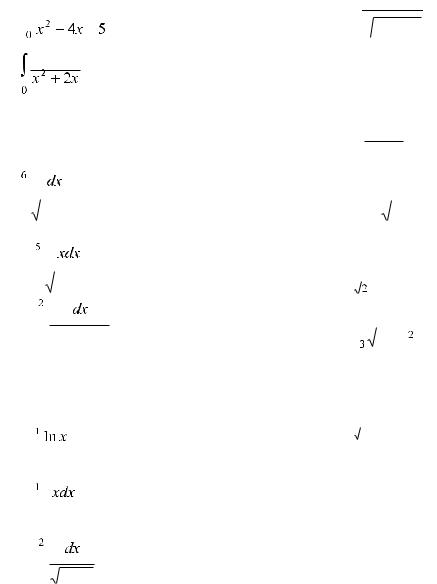
1 |
dx |
|||
6 |
||||
|
|
|
||
2
7 dx
8 |
|
|
3 |
|
|
|
||
8 |
|
x dx |
||||||
2 |
x2 4 |
|
||||||
|
|
|
|
|
|
|
||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
||||||
1 |
|
|
|
|||||
10 |
|
|
|
|
|
|||
|
|
|
|
|
||||
|
|
x2 1 |
||||||
|
|
1 |
|
|
|
|||
11 2 sin 2 x
|
0 |
|
|
|
xdx |
|
||||
12 |
|
|
|
|
||||||
|
|
3x 5 |
||||||||
|
|
|
|
|
|
|||||
|
5 |
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
|||
13 |
|
|
|
|
|
|
dx |
|||
|
|
|
|
x |
|
|||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
x4 |
1 |
||||||||
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
2 x |
|||||
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
||||
4 xdx
21
0  16 x 2
16 x 2
2
22 (tgx ctgx)dx
0
1 x2dx
23 1 x2 1
|
1 |
|
|
|
arcsin 2xdx |
||||||||||||
24 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
1 |
|
|
|
|
1 4x 2 |
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
xdx |
|
|
|
|
|
|||||
25 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
2x 2 4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
9 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
26 |
|
|
|
|
|
|
x |
|
|
dx |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
9 |
x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x2 |
3x |
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
28 |
|
5 |
|
|
|
|
x |
|
|
|
|
|
|||||
|
|
|
|
|
dx |
||||||||||||
|
0 |
|
|
|
x2 5 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
dx ln2(x 1) |
|||||||||||||
29 |
|
|
|
|
|
|
x 1 |
||
1 |
|
|
||
|
|
|
|
|
9 ln( x 3)dx |
||||
30 |
|
|
|
|
|
3x 9 |
|||
3 |
|
|
||
|
|
|
|
|
|
Paydalanılǵan ádebiyatlar dizimi |
|
1 |
Azlarov T.A., Mansurov X.T. |
Matematik analiz |
|
|
1,2 qism“O’qituvchi” 1994, 1995 |
2 |
Xudaybergenov G, Vorisov A, |
Matematik analiz 1,2 qism Karshi 2004 y. |
|
Mansurov X |
|
3 |
İlin V.A., Sadovnichiy V.A., |
Matematicheskiy analiz 1,2 t. M., “Nauka” |
|
Sendov B.X. |
1979 |
4 |
Sa`dullaev A,Xudaybergenov G, |
Matematik analiz kursidan misol va |
|
Mansurov X.T. Varisov A.K. |
masalalar tuplami Toshkent “O’qituvchi” |
|
|
1-2 q. 1993, 1995 |
5 |
Demidovich B.P |
Sbornik zadach i uprajnenii po matemat. |
|
|
Analizu Moskva 1990 |
6 |
Zorich V.A. |
Matematicheskiy analiz 1,2 t. M. “Nauka” |
|
|
1981 |
