
Aniq integrallar
.pdf
joqarǵı yamasa tómengi shegi ózgeriwshi bolǵan anıq integrallardıń shegi bolıwın atap ótemiz.
|
|
|
|
Eger |
f x funkciya |
|
a,b te úzliksiz teris emes anıqlanǵan hám |
x b |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
noqattıń dógereginde shegeralanbaǵan funkciya bolsa, onda f x dx |
menshiksiz |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
integralı |
|
jıynaqlı bolǵan jaǵdayda bul integraldıń mánisin tómennen |
Ox |
|||||||||||||||||||||||||||||
kósheriniń |
[a, b) |
yarım segmenti menen, shep hám oń tárepten x a , |
x b |
|||||||||||||||||||||||||||||
tuwrıları, |
joqarıdan |
y f x funkciyasınıń grafigi menen shegaralanǵan 12- |
||||||||||||||||||||||||||||||
súwrettegi kórsetilgen figuranıń maydanı dep qabıl etiw múmkin. |
|
|
|
|||||||||||||||||||||||||||||
1-mısal |
|
y |
|
1 |
|
|
|
|
funkciyasın |
0;1 segmentinde |
qarastıramız. |
0 1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ushın |
|
|
0, |
|
|
|
|||
shártin |
|
qanaatlandıratuǵın |
hár |
bir |
|
|
segmetinde |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2(1 |
1 ) anıq |
integralın esaplap, |
1 0 |
1 x |
mánisine iye |
||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
dx |
|
|
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
bolamız, |
yaǵnıy |
|
|
|
2. Demek |
14-súwretdegi |
|
shtrixlanǵan |
figuraniń |
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
1 x |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
maydanı 2 ge teń dep qabıl etiw mumkin. Shegaralanbaǵan funkciyalardıń basqa tipleri ushında usıǵan uqsas geometriyalıq maǵana beriwge boladı.
|
|
|
|
|
|
|
|
|
|
|
14- suwret |
|
||||
|
1 |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 mısal. |
|
|
, 0 menshiksiz integralın jıynaqlılıqqa izertleń. |
|||||||||||||
|
||||||||||||||||
|
0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
Sheshiliwi: 0;1 ushın |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
x |
1 |
|
1 |
|
1 |
1 |
, eger 1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 dx |
|
|
|
|
|
|
1 |
|
1 |
|||||
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
ln x 1 |
ln , |
eger 1 |
|
||||||||
|
|
|
|
|
|
|
|
|
bolıp, bunnan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 dx |
1 |
, eger |
1 |
||
|
|
|
||||||
|
|
lim |
|
|
|
1 |
|
|
|
|
x |
|
|||||
|
|
x |
, eger 1 |
|||||
|
|
|
|
|
|
|
|
|

1 |
dx |
menshiksiz integral 1 bolǵanda jıynaqlı hám |
|
|
boladı. Demek |
|
|
1 |
|
x |
|
|||
0 |
|
|
|
|
mánisleri ushın tarqalıwshı boladı.
Anıq integrallarǵa tiyisli bir neshe qásiyetlerdi shegaralanbaǵan funkciyalardiń menshiksiz integralı jaǵdayına ulıwmalastırıw mumkin.
Dara jaǵdayda bunday menshiksiz integrallar ushın Nyuton-Leybnic
formulası tómendegishe ulıwmalasadı. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Meyli |
|
f (x) |
funkciyası |
a,b yarım segmentte úzliksiz hám |
||||||||||||||||||
b , a,b , |
0 |
intervalda |
shegaralanbaǵan bolsın. |
F(x) arqalı |
f (x) |
|||||||||||||||||
funkciyasınıń a,b |
yarım |
segmentindegi |
baslanǵısh |
funkciyasın |
belgilep, |
|||||||||||||||||
a,b ushın Nyuton-Leybnic formulasına sáykes |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx F F a F (x) |
|
|
|
teńligin jazıw mumkin. |
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bunnan |
f (x)dx |
menshiksiz integralı bar bolıwı ushın |
lim F |
sheginiń |
||||||||||||||||||
|
b 0 |
|||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bar bolıwı zárúrli hám jeterli. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Eger usı shek bar bolsa, onda onı |
F b 0 túrinde belgilep |
|
|
|
||||||||||||||||||
b |
|
|
|
|
|
b 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f x dx F x |
|
a |
F b 0 F a |
formulasina iye bolamız. |
|
|
||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Usı formulanı anıq integral ushın Nyuton-Leybnic formulasınıń qarastırılıp |
||||||||||||||||||||||
atırǵan tiptegi menshiksiz integrallarǵa ulıwmalasqanı boladı. |
|
|
|
|||||||||||||||||||
Usıǵan |
uqsas |
a;b da úzliksiz, biraq |
a;a a;b |
intervalda |
||||||||||||||||||
shegaralanbaǵan |
f x funkciyası ushın |
a;b daǵı bazıbir dáslepki funkciyasın |
||||||||||||||||||||
F x arqalı |
belgilep, |
lim F |
|
bunda a b |
shekli shegi bar |
bolǵan |
||||||||||||||||
a 0 |
|
|
||||||||||||||||||||
jaǵdayda Nyuton-Leybnic formulasın |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
f x dx F x |
a |
0 |
F b F a 0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
túrinde jazamız. Bunda F a 0 lim F |
|
|
|
|
|
|
||||||||||||||||
|
|
f x funkciya a;b |
a 0 |
|
|
|
|
|
|
|
|
|
||||||||||
Endi |
tiń shekli sandaǵı |
x1 , x2 , |
noqatlarınan |
|||||||||||||||||||
basqa |
hárbir |
noqatında |
úzliksiz |
bolıp, |
xi , i 1,2, |
m |
noqatlardıń |
jaqınında |
||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
shegaralanbaǵan bolsa, onda |
f x dx |
|
|
menshiksiz integralı ushın |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
x1 |
|
|
|
x2 |
|
|
|
b |
|
|
|
|
||||
|
|
|
|
f x dx f x dx f x dx |
f x dx |
|
|
|||||||||||||||
|
|
|
|
a |
|
a |
|
|
|
x1 |
|
|
|
xm |
|
|
|
|
||||
teńligi orınlı boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

|
Eger |
|
|
de |
|
úzliksiz |
hám |
|
|
|
ushın |
a; x1 , x1; x2 , |
|
||||
|
|
a;b |
|
|
|
|
|
|
|
f |
|
x |
|
|
|
|
|
kesindilerinde |
dáslepki |
funkciyası |
F x |
bar |
bolsa, |
onda Nyuton-Leybnic |
|||||||||||
formulasınan paydalanıp aqırǵı teńlikti |
|
|
|
|
|
|
|
||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x dx F x1 |
0 F a |
|
F x2 |
0 F x1 0 |
|
F xm 0 F b túrinde |
|||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jazıwǵa boladı. Onda |
F |
|
x |
funkciya |
a;b |
|
|
|
|
|
|
||||||
|
|
|
te úzliksiz ekenliginen hám |
|
|||||||||||||
|
|
F xi 0 F xi 0 0, |
i 1,2, |
|
|
|
|
|
|||||||||
teńligin esapqa alıp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f (x)dx F (x) b |
F (b) F (a). |
|
|||||||||||
a
túrindegi Nyuton-Leybnic formulasına iye bolamız.
§4. Menshiksiz integrallarda ózgeriwshilerdi almastırıw |
|
|
|
|||||||||||
Eger f x funkciya |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a;b |
|
te úzliksiz, |
al x |
|
t |
|
funkciya |
; |
|
te |
|||
úzliksiz differenciyalanıwshı, |
|
qatań |
monoton |
hám |
|
a, |
lim t |
b |
||||||
|
|
|
|
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
shártleri orınlı bolıp, f x dx, |
f t t dt |
integralarınıń keminde birewi |
||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jıynaqlı bolǵanda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
x dx f t t dt |
|
|
|
|
|
|
(*) |
||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńligi orınlı boladı. Usı teńlik menshiksiz integrallarda ózgeriwshilerdi almastırıw formulası dep ataladı.
Haqıyqatında da meyli , , t bolsın. Onda 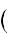
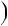 b
b
boladı. Endi anıq integralda ózgeriwshilerdi almastırıw formulasınan paydalanıp, |
|||||||
|
|
|
|
|
|
|
|
f x dx |
f t t dt |
teńligin jazamız. t funkciyası qatań monoton |
|||||
a |
|
|
|
|
|
|
|
hám ; te úzliksiz ekenliginen, onıń keri funkciyası a;b te qatań monoton |
|||||||
|
|
|
|
|
|
t t dt |
|
hám úzliksiz ekenligi kelip shıǵadı. Onda |
lim |
f |
shektiń shekli |
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ekenliginen |
lim f x dx |
shegi shekli hám (*) teńligi orınlı ekenligi kelip shıǵadı. |
|||||
|
b 0 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
Eskertiw. t funkciyası |
, , |
|
kesindide qatań kemeyiwshi, |
||||
|
|
|
|
|
|
||
úzliksiz differencialanıwshı hám |
a lim t |
b lim t |
bolǵan jaǵdayda |
||||
|
|
|
t 0 |
|
|
t b 0 |
|
ǵana orınlı boladı.
Bul jaǵdayda anıq integral qásiyetine sáykes bolǵanda
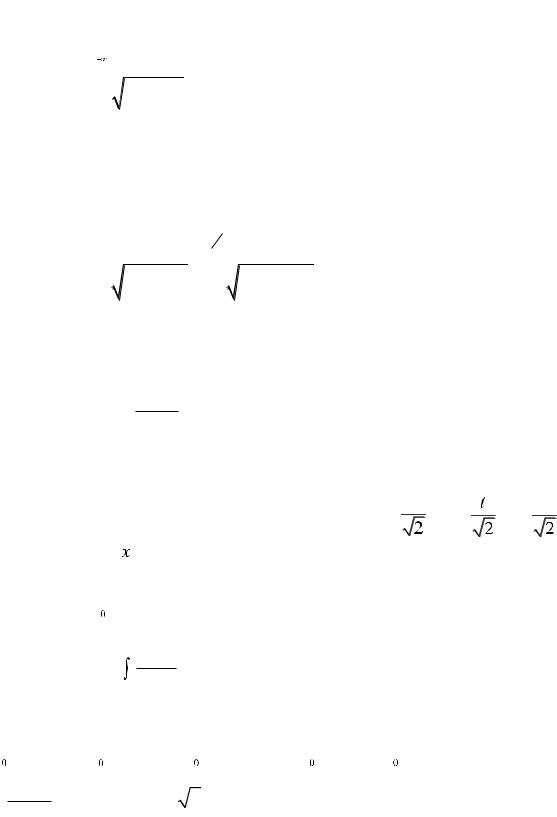
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g t dt g t |
dt |
|
|
teńliginen paydalanadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
integralın esaplań. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1-mısal. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Sheshiliwi: |
|
x tgt, 0 t |
|
|
formulaǵa sáykes ózgeriwshilerdi almastırsaq, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dx |
|
|
dt |
boladı hám x 0 t 0; x t |
bolǵanı ushın |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
costdt sin t |
|
2 |
1. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 1 3 |
|
|
tg2t 1 3 |
|
|
0 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 |
1 |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2-mısal. |
0 |
|
|
|
|
|
|
|
|
|
integralın esaplań. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x4 |
|
1 |
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 dx |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Sheshiliwi: |
|
x |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
|
t; |
|
|
|
|
|
|
|
|
|
x t |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
dt |
|
2 |
arctg |
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 t |
|
|
|
|
|
|
|
t |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
dt d x |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3-mısal. |
|
|
|
|
|
|
|
|
|
integralın esaplań. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
x |
|
|
|
||||||
|
|
|
Sheshiliwi: |
t |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
4 |
1 |
|
|
|
|
|
1 |
||||||||||
|
|
|
0 |
x |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
t2 1 |
|
|
|
|
dt |
t 2 |
|||||||||
|
|
t |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
dt |
|
|
|
||||||||
|
1 t |
4 |
t |
4 |
|
1 |
|
|
|
|
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 t . |
||||||||||||
|
|
|
4dx |
|
t |
2 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
dt 2 . |
|
|
||||||||||
|
x |
1 |
|
4 |
|
1 |
|
|
|||||||||||||||
0 |
|
|
|
|
|
0 t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x t 0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|||||||
dt |
x 0 t |
|
t |
1 |
t |
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dx |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
Endi |
|
|
|
|
|
|
teńligin esapqa alıp |
|||||||||||
|
4 |
|
4 |
1 |
||||||||||||||
|
|
x |
1 |
|
t |
|
|
|
|
|
|
|
|
|
|
|||
§5. Teńsizliklerdi integrallaw
Menshiksiz integrallarǵa baylanıslı kóplegen máselelerde qarastırılıp atırǵan integrallardıń mánislerin tabıw integrallardı esaplawǵa baylanıslı qıyınshılıqlarǵa
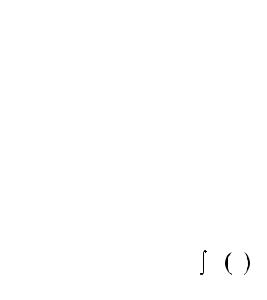
alıp keliwi múmkin. Bunday jaǵdaylarda menshiksiz integrallardıń jıynaqlı bolıwın kórsetiw menen shegaralanadı, al integraldıń mánisin tabıw talap etilmeydi.
Usıǵan baylanıslı menshiksiz integrallardıń jıynaqlılıq belgileri úyreniledi.
1-teorema. (menshiksiz integrallardıń jıynaqlı bolwınıń zárúrli shárti) Eger
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x dx |
menshiksiz integralı jıynaqlı bolsa, onda |
a;b ushın f x dx |
||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
shegaralanǵan boladı. Yaǵnıy M 0 |
sanı tabılıp a;b ushın |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x dx |
|
M |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizligi orınlı boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bul teoremadaǵı tastıyıqlawdıń |
|
durıslılıǵı |
f x dx |
menshiksiz integralı |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jıynaqlı bolǵanı ushın |
lim |
f |
x |
|
dx shekli sheginiń bar bolıwınan kelip shıǵadı. |
|||||||||||||||||
|
|
b 0 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-teorema. (Koshi belgisi) |
|
f x dx |
menshiksiz integralı jıynaqlı bolıwı |
|||||||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ushın qálegen 0 |
sanına sonday |
|
a;b sanı bar bolıp, |
, |
|
|
;b |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
mánislrinde |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x dx |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizliginiń orınlı bolıwı zárúr hám jeterli. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||
Dálilleniwi: (Zárúrligi) |
Meyli |
|
|
f x dx |
menshiksiz |
integralı |
|
jıynaqlı |
||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bolsın. Onda F f x dx |
funkciyasınıń b 0 |
da shekli shegi bar boladı. |
||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 sanına |
||||
Onda funkciyaniń shegi bar bolıwınıń Koshi belgisine sáykes |
||||||||||||||||||||||
sonday |
a,b sanı bar boladı da , ,b ushın |
|
|
|
|
|
|
|||||||||||||||
|
|
F ( ) F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
f (x)dx |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizligi orınlanadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Jeterliligi: 0 |
|
|
|
|
a,b sanı bar |
|
|
|
|
|
||||||||||||
sanı |
ushın |
bolıp |
f x dx |
|
||||||||||||||||||
|
, ,b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizligi |
|
mánislerinde |
orınlı |
bolsın. |
Bul |
teńsizlik |
||||||||||||||||
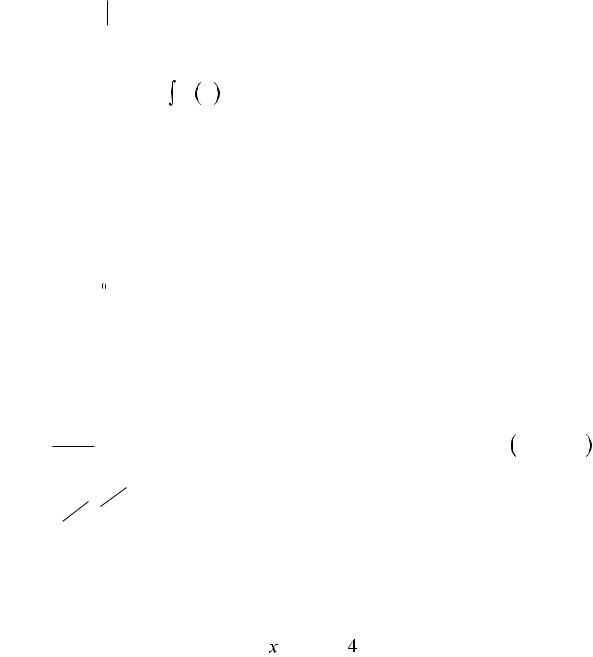
|
F ( ) F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
teńsizligine teń kushli, yaǵnıy |
F ( ) f x dx |
funkciyası |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
ushın |
b 0 |
da shekli shegi bar bolıwı haqqıdaǵı Koshi belgisi orınlanǵan. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
||
Onda |
|
lim F ( ) lim |
f |
|
|
x |
dx |
shekli |
|
shegi |
|
bar. Bul f x dx |
|
menshiksiz |
|||||||||||||||||||||||||||||||||||
|
b 0 |
|
|
|
|
|
|
|
|
b 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
integraldiń jıynaqlı bolıwın kórsetedi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eskertiw: |
|
f x dx |
menshiksiz |
integralı |
|
|
tarqalıwshı |
|
boladı, |
eger |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
menshiksiz |
integrallar |
ushın |
Koshi belgisi orınlanbaǵan bolsa, yaǵnıy sonday |
||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
0 |
|
sanı |
|
|
|
tabılıp, |
|
|
a,b |
sanına |
, |
,b |
sanları |
bar |
bolıp |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f x dx |
|
teńsizligi orınlı bolsa. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Mısal. |
|
|
|
|
|
|
|
|
|
|
dx integralın jıynaqlılıqqa tekseriń. Bunda 1 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sheshiliwi: 1 sanına sonday n N sanı bar boladı da n |
|||||||||||||||||||||||||||||||||||||||||||||
teńsizligi orınlanadı. Onda |
|
n |
|
da |
|
2 n |
|
mánislerin alsaq, |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2n sin2 x |
|
|
|
|
|
sin2 x |
|
|
|
|
1 |
|
|
|
|
|
1 2n |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
2n |
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|
dx |
2n |
|
|
sin |
|
xdx |
4n |
|
|
1 cos 2x dx |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
n |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 n |
|
|
|
|
4 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
yaǵnıy |
|
|
|
|
|
bolǵanda, |
|
1 |
|
|
sanı |
|
ushın |
|
|
n N |
|
sanı |
bar |
bolıp |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n |
, |
|
|
|
|
2n |
; |
|
|
|
|
|
mánislerinde |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizligi orınlı bolǵanı ushın berilgen integral tarqalıwshı boladı.
§6. Teris emes funkciyalardıń menshiksiz integralları.
Teorema 1. |
Eger x a;b |
ushın |
f x 0 |
teńsizligi |
orınlı |
|
b |
|
|
|
|
|
|
bolsa, onda f x dx |
menshiksiz |
integralı |
jıynaqlı |
bolıwı |
ushın |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
F f x dx, a b |
funkciyasınıń joqarıdan |
shegaralanǵan bolıwı |
zárúr |
|||
a |
|
|
|
|
|
|
hám jeterli.

|
|
|
|
|
|
|
b |
x dx |
|
|
|
|
|
|
|
Dálilleniwi. Zárúrligi. Meyli |
f |
menshiksiz integralı jıynaqlı bolsın. |
|||||||||||
Onda 1 , 2 a;b ushın |
|
a |
|
|
|
|
|
|
|
|||||
teńsizliginen |
|
|
|
|||||||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
2 |
|
|
|
|
|
|
F 2 F 1 f |
x dx f |
x dx f x dx 0 |
|
|
|||||||
|
|
|
|
|
|
a |
|
|
a |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizligi |
kelip |
shıǵadı. |
Demek, |
F f x dx ósiwshi |
funkciya. Onda |
|||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
monoton |
funkciyalardiń |
|
shegi |
|
haqqındaǵı |
teoremaǵa |
sáykes |
|||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f (x)dx sup F( ) C |
|
shekli |
shegi |
bar boladı |
hám supremumniń |
|||||||||
b 0 |
a |
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
anıqlamasına sáykes a,b ushın |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
f (x)dx f (x)dx C |
|
|
|
||||||
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizligi orınlı, yaǵnıy |
f (x)dx F ( ) |
funkciyası shegaralanǵan. |
|
|||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jeterliligi: |
Meyli |
F f x dx |
funkciya |
joqarıdan shegaralanǵan |
bolsın, |
|||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńligi orınlı bolsın. F ósiwshi hám |
||||||
yaǵnıy C : a,b f (x)dx C |
||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
joqarıdan |
|
shegaralanǵan |
|
|
funkciya |
bolǵanı |
ushın |
|||||||
lim F F b 0 sup F |
shekli shegi bar boladı. Bunnan menshiksiz |
|||||||||||||
b0 |
|
|
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
integralınıń jıynaqlı bolıwı anıqlaması tiykarında |
f x dx |
integralı jıynaqlı dep |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
juwmaq shıǵaramız. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2-teorema. (Salıstırıw |
belgisi). Eger |
x a;b ushın |
0 f x g x |
||||||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
teńsizligi |
orınlı |
bolsa, onda |
J1 g x dx |
menshiksiz |
integralınıń |
jıynaqlı |
||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
bolıwınan |
J2 f x dx |
menshiksiz integralınıń jıynaqlı bolıwı kelip shıǵadı, al |
||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
J2 integraldıń tarqalıwshı bolıwınan |
J1 integralınıń da tarqalıwshı bolıwı kelip |
|||||||||||||
shıǵadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dálillew: Meyli J1 |
integralı |
jıynaqlı bolsın. Onda anıq integraldıń |
|||||||||||
teńsizliklerge baylanıslı qásiyeti tiykarında |
f x g x teńsizliginen |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x dx g x dx |
|
|
|
|||||
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
teńsizligi a;b ushın orınlı boladı hám 1-teoremaǵa sáykes |
|
|
||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
lim g(x)dx J1 |
sup |
g(x)dx |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
b 0 |
|
|
|
|
a b |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
shekli shegi bar. Bunnan x a;b ushın |
f (x)dx J1 |
teńsizligi orınlı. Onda 1- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teoremaǵa sáykes |
J2 -integralı jıynaqlı degen juwmaq shıǵadı. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Meyli |
|
J2 |
f x dx menshiksiz |
integral |
|
|
tarqalıwshı |
bolsın. |
Onda |
||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J1 g x dx |
jıynaqlı bola almaydı. Sebebi, eger |
J1 |
integral jıynaqlı bolǵanda |
|||||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teoremaniń birinshi bólimine sáykes |
J2 |
integral da jıynaqlı bolar edi. |
|
|
|
|||||||||||||||||||||||||||
Saldar. Eger |
x a,b |
ushın |
f (x) 0 , |
|
g(x) 0 |
teńsizlikleri |
orınlı hám |
|||||||||||||||||||||||||
x b 0 |
da |
f (x) |
|
|
|
|
bolsa, onda |
J1 |
|
hám J2 menshiksiz integralları |
||||||||||||||||||||||
yamasa bir waqıtta jıynaqlı, yamasa bir waqıtta tarqalıwshı boladı. Haqıyqatında |
||||||||||||||||||||||||||||||||
da berilgen shártlerde |
lim |
f (x) |
1 boladı. Onda shektiń anıqlamasına sáykes |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
b 0 g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 a,b : x ,b |
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizligi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dep tayınlap bul teńsizlikti |
x 1/ 2 ,b ushın |
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1 f (x) 3 1 g(x) f (x) 3 g(x) |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
g(x) |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
turinde jazıp alamız. |
f (x) hám g(x) funkciyaları |
a,b yarım segmentinde |
||||||||||||||||||||||||||||||
ayırıqsha noqatlarına iye emes. Onda |
J1 , J2 |
integralları |
jıynaqlı |
bolıwı |
ushın |
|||||||||||||||||||||||||||
f (x) |
hám |
g(x) |
|
funkciyalarınıń |
c,b |
a,b |
yarım segmenti |
boyınsha |
||||||||||||||||||||||||
integrallarınıń jıynaqlı bolıwı zárur hám jeterli boladı. Demek, eger |
J1 |
integral |
||||||||||||||||||||||||||||||
jıynaqlı bolsa, onda salıstırıw belgisinen hám sońǵı teńsizliktiń oń tárepin esapqa |
||||||||||||||||||||||||||||||||
alǵan |
halda |
|
J2 |
integralı |
jıynaqlı, al |
eger |
|
J2 |
integralı |
jıynaqlı |
bolsa |
sońǵı |
||||||||||||||||||||
teńsizliktiń shep tárepinen hám salıstırıw belgisinen |
J1 integralı da jıynaqlı degen |
|||||||||||||||||||||||||||||||
juwmaq shıǵadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Eger |
J1 |
integral jıynaqlı bolmasa, |
onda |
salıstırıw |
belgisinen |
hám |
sońǵı |
||||||||||||||||||||||||
teńsizliktiń shep tárepin esapqa alǵan halda |
J2 integralı tarqaluwshı, al eger J2 |
|||||||||||||||||||||||||||||||
integralı jıynaqlı bolmasa sońǵı teńsizliktiń oń tárepinen hám salıstırıw belgisinen J1 integralı da tarqaluwshı dep juwmaq shıǵaradı.
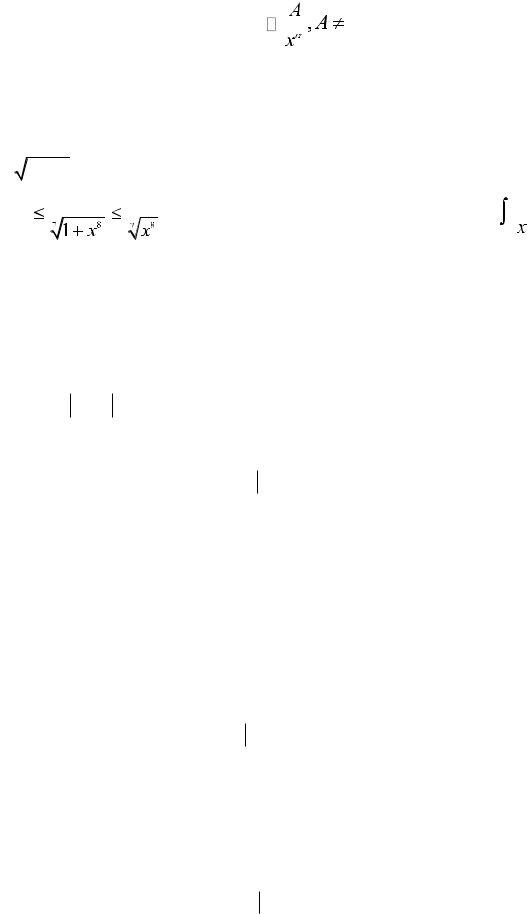
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dara jaǵdayda |
x da f (x) |
|
|
|
|
|
0 |
bolsa, |
onda |
f (x)dx |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 mánislerinda |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|||||
menshiksiz |
|
integralı |
|
|
jıynaqlı, |
al 1 mánislerinda |
||||||||||||||||||||||
tarqalıwshı boladı. Bunda |
|
f (x) |
funkciyası |
|
a, |
|
segmentinde |
a |
ushın |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
anıq integral maǵanasında integrallanıwshı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1-mısal. |
|
sin x |
|
dx |
integralın jıynaqlılıqqa tekseriń. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
7 1 x8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Sheshiliwi: |
0 |
sin4 |
x |
1 |
|
teńsizligi x 1 mánislerinde orınlı hám |
|
dx |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
8/7 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
integralınıń |
jıynaqlı |
bolıwınan salıstırıw belgisi |
tiykarında |
berilgen |
integral |
|||||||||||||||||||||||
jıynaqlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§7. Menshiksiz integrallardıń absolyut hám shártli jıynaqlılıǵı.
|
b |
1-anıqlama. |
J f (x)dx menshiksiz integralı absolyut jıynaqlı dep |
|
a |
b
ataladı, eger G f (x) dx integralı jıynaqlı bolsa.
a
Teorema. Hár qanday absolyut jıynaqlı integral jıynaqlı boladı hám
|
|
|
|
b |
b |
|
|
|
|
|||
|
|
|
|
f (x)dx |
|
f (x) |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
|
|
|
|
|||
teńsizligi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
Dálilleniwi: G integralı jıynaqlı bolǵanı ushın Koshi belgisine sáykes |
|
|
||||||||||
teńsizligi orınlı |
boladı. |
Menshiksiz |
integraldiń anıqlamasına |
sáykes |
f (x) |
|||||||
funkciyası shetki noqatları |
|
|
|
|
|
|
|
|
|
|
|
|
|
, bolǵan kesindide integrallanıwshı, sonıń ushın |
|||||||||||
|
|
|
|
|
f (x) |
|
||||||
bul funkciya usı |
kesindide |
absolyut |
integrallanıwshı boladı, |
yaǵnıy |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
funkciyası da anıq integral maǵanasında integrallanıwshı. Endi anıq integraldı bahalaw qaǵıydasına sáykes
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|||||||||||
|
f (x)dx |
|
|
f (x) |
|
dx |
|
|
|||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizligi orınlı bolǵanı ushın |
f (x)dx funkciyası Koshi belgisi shártlerin |
||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||
qanaatlandıratuǵınlıǵın kóremiz. Bul J |
integralı jıynaqlı bolıwı ushın zárur hám |
||||||||||||||
jeterli. Endi anıq integraldı bahalaw qaǵıydasın paydalanıp, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
||||||||||||
|
|
|
f (x)dx |
|
f (x) |
|
dx |
||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
a |
|
|
|
|
a |
|||||||

teńsizligin jazıw mumkin. Bul teńsizlik |
|
|
a,b ushın orınlı bolıwı málim. J |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
hám G integralları jıynaqlı ekenligin esapqa alıp keyingi teńsizlikte |
b 0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
shekke ótsek, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
|
f (x) |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizligine iye bolamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2- anıqlama. J |
integralı jıynaqlı, bıraq G integral tarqalıwshı bolsa, onda |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
J integralı shártli jıynaqlı dep ataladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Mısal. |
|
|
|
|
dx |
integralın jıynaqlılıqqa hám absolyut jıynaqlılıqqa tekseriń. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
||||||||||||
1). |
Eger |
|
1 |
|
|
|
bolsa, |
|
|
onda |
|
x 1 |
|
|
mánislerinde |
0 |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
teńsizliginen |
hám |
|
|
|
|
|
|
|
menshiksiz integralınıń jıynaqlı |
bolıwınan, salıstırıw |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
belgisine |
sáykes G |
|
|
|
|
|
|
|
|
|
|
dx |
integralınıń |
jıynaqlı |
|
bolıwın |
kóremiz, |
yaǵnıy |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
berilgen integral absolyut jıynaqlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2). Eger 0;1 bolsa, onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
cos x |
|
|
|
u |
|
|
|
|
du |
|
|
|
dx |
|
|
sin x |
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
dx, |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
x |
|
|
|
cos xdx dv v |
sin x |
|
|
|
x |
|
1 |
|
|
1 |
x1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
bunda lim |
|
|
|
|
|
0; |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
hám |
|
|
|
menshiksiz |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
integralınıń |
jıynaqlı |
bolǵanı ushın |
|
|
1 |
|
|
|
dx |
|
|
integralınıń |
absolyut |
jıynaqlı |
||||||||||||||||||||||||||||||||||||||||||
|
|
x1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
bolıwınan bul integraldıń ozi de jıynaqlı ekenligin kóremiz. |
|
1 cos 2x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||
Endi |
|
|
|
dx |
|
|
integralın tekseremiz. |
|
|
cos x |
cos x |
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
teńsizliginen hám
1
tarqalıwshı boladı.
1 |
|
integralınıń tarqalıwshı ekenliginen |
||||
|
dx |
|||||
x |
||||||
|
|
|
|
|
||
Demek, 0,1 mánislerinde |
|
|
|
|||
|
|
|
|
x |
|
|
|
|
|
1 |
|
||
|
|
cos x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
dx integralı |
|
|
|
||||
|
|
x |
|
|
||
1 |
|
|
|
|
|
|
integral shártli
jıynaqlı.
