
Aniq integrallar
.pdf
5. |
1 ( 1 ) |
iymeginiń |
|
1 3 |
|
segmentine |
sáykes |
keliwshi |
doǵası |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
uzınlıǵın tabıń.(J. 2 |
1 |
ln 3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aylanba |
betliktiń |
maydanı: 1. |
x a cos3 t, y a sin3 t |
|
parametrli teńlemesi |
||||||||||||||||||||||||||||||||||||||||
menen berilgen astroydanıń y x |
tuwrisı dógereginde aylanıwında payda bolǵan |
||||||||||||||||||||||||||||||||||||||||||||
betlikktiń betiniń maydanın tabıń. |
|
|
3 a2 |
1)). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
(J. |
|
|
|
|
|
|
(4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. (x 2)2 y2 1 dóńgelegi OY |
kósheri dógereginde aylanıwında payda bolǵan |
||||||||||||||||||||||||||||||||||||||||||||
tordıń betiniń maydanın tabıń. (J. 8 2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3. |
|
|
y x |
|
x |
|
,0 x a |
iymeginiń OX |
kósheri dógereginde aylanıwında payda |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
bolǵan betlikktiń betiniń maydanın tabıń. (J. |
4 a2 |
(21 3 |
2ln |
|
3 |
13 |
). |
|
|
||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
243 |
|
|
|
|
|
|
|
|
|||
4. |
y2 2 px, 0 x a |
parabolası OX |
|
kósheri dógereginde aylanıwında payda |
|||||||||||||||||||||||||||||||||||||||||
bolǵan betlikktiń betiniń maydanın tabıń. (J. 2 (( p 2a) |
|
|
|
|
|
p2 )). |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
5. x3 y 3 |
|
a 3 astroydası OX |
kósheri dógereginde aylanıwında payda bolǵan |
||||||||||||||||||||||||||||||||||||||||||
betlikktiń betiniń maydanın tabıń. (J . |
12 |
a2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
y a ch x , |
|
x |
|
b iymegi |
OX hám OY |
kósherleri dógereginde aylanıwında |
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
payda |
|
|
|
bolǵan |
|
|
|
betliklerdiń |
|
|
|
betiniń |
|
|
maydanın |
tabıń. |
|||||||||||||||||||||||||||||
(J. a(2b ash 2b); |
2 a(a bsh b ach b)). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Deneniń |
kólemin |
tabıń. 1. |
y b( x)23 |
|
, 0 x a |
teńlemesi menen |
berilgen |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
iymek sızıǵı neyloyd dep ataladı. Neyloyd OX |
kósheri dógereginde aylanǵanda |
||||||||||||||||||||||||||||||||||||||||||||
payda bolǵan betlk penen shegaralanǵan deneniń kólemin tabıń. |
(J. |
3 |
ab2 ). |
||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|||
2. y 2x x2, y 0 |
sızıqları |
menen |
|
shegaralanǵan figura OY |
kósheri |
||||||||||||||||||||||||||||||||||||||||
dógereginde aylanǵanda payda bolǵan deneniń kólemin tabıń. (J. 2 2 ). |
|
||||||||||||||||||||||||||||||||||||||||||||
3. Biyikligi h , ultanınıń maydanı S bolǵan piramidanıń kólemin tabıń. (J. |
1 |
S h) |
|||||
|
|||||||
|
|
|
|
|
3 |
||
4. Tómende berilgen sızıqlar menen shegaralanǵan figuralar OX |
|
hám OY |
|||||
kósherleri dógereginde aylanıwınan payda bolǵan denelerdiń kólemlerin tabıń. |
|||||||
1. y ex , x 0, x 1, y 0. (J . |
(e2 1) |
, 2 |
2. y x3, y 1, x 0. (J. |
6 |
, 3 ) ; |
||
|
|
||||||
2 |
|
|
7 |
5 |
|||

3. y |
1 |
, x 1, x 1, y 0. (J . ( 2) , ln 2). 4. |
|
y sin x, 0 x |
|
2 |
|
|
|||||||
|
|
2 |
|
||||||||||||
|
1 x2 |
|
4 |
|
|
|
|
|
|
|
, y 0. (J. |
2 , 2 |
|
) |
|
5. |
y ln x, y 0, x e |
sızıqları |
menen |
shegaralanǵan |
figuranıń |
||||||||||
y 1, x 1, x 1, y 1 |
tuwrılarınıń |
hárbiriniń |
dógereginde |
aylanıwında |
|||||||||||
payda bolǵan denelerdiń kólemlerin tabıń. (J. e, |
|
(e2 3) |
(e2 5) |
, (4 e)). |
|
|
|||||||||
|
|
|
, |
|
|
|
|
|
|||||||
2 |
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. (x 2)2 y2 1 dóńgelegi OY kósheri |
dógereginde |
aylanıwında payda |
|||||||||||||
bolǵan tordıń kólemin tabıń. (J . ).
Anıq integraldıń fizikalıq qollanıwları: 1.Birlik massalar jaylastırılǵan ush materiallıq noqatlar sistemasınıń awırlıq orayı usı noqatlar tóbeleri bolǵan ushmúyeshliktiń medianalarınıń kesilisiw noqatında bolıwın dálilleń.
2. Konustıń qaptal betiniń maydanın tabıń. (J. Rl)
3. x2 y2 r |
2, y 0 dóńgeleginiń awırliq orayınıń koordinatasın tabıń.(J.(0, |
4r |
)). |
||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
4. |
y |
|
r 2 x2 , r x r tómengi yarım |
tegislikte jaylasqan yarım |
|||||||
sheńberiniń awırliq orayınıń koordinataların tabıń. |
(J.(0, |
2r |
)). |
|
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Massası |
|
m bolǵan hám y 2x, x 3, y 0 |
tuwrıları menen shegaralanǵan |
|||||||
úshmúyeshliginiń OY kósherine baylanısli inerciyaıq momentin esaplań. |
|||||||||||
6. |
Massası |
|
m bolǵan x2 y2 r2 |
sheńberiniń OY kósherine |
baylanısli |
||||||
inerciyaıq momentin esaplań. |
|
|
|
|
|
|
|
||||
7. Massası m bolǵan 0 x a, 0 y b tuwrımúyeshli plastinanıń OY |
kósheriniń |
||||||||||
dógereginde múyeshlik tezliginde aylanǵandaǵı kinetikalıq energiyasın esaplań.
8. Yarım kósherleri a hám b bolǵan birtekli elliptikalıq plastinkanıń simmetriya |
||||||||||
|
ab3 |
|
a3b |
|
|
|
|
|||
kósherlerine baylanıslı inerciyalıq momentlerin esaplań.(J. |
|
|
, |
|
|
) . |
|
|
|
|
4 |
|
4 |
|
|
|
|
||||
9. Biyikligi h , ultanınıń radiusı r bolǵan birtekli konustıń |
|
ultan tegisligine |
||||||||
baylanıslı statikalıq momentin hám inerciyalıq momentin tabıń. (J . |
r 2h2 |
|
r 2h3 |
|||||||
|
, |
|
|
). |
||||||
|
|
|||||||||
|
|
|
|
12 |
|
30 |
|
|||
10. Koordinata basına jaylastırılǵan e1 elektr zaryadı ózi menen bidey tańbali e2 elektr zaryadın iterip x a noqatınan x b noqatına ótkeredi. e2 zaryadın
x a |
|
noqatınan |
x b noqatına ótkeriwde |
F kúshiniń islegen jumisin tabıń. |
||||
(J . ke e |
( |
1 |
|
1 |
) . |
|
|
|
|
|
|
|
|||||
1 |
2 |
|
a |
b |
|
|
||
11. Eger prujinanı |
x metrge sozatuǵın kúsh |
F kx hám prujinanı 0,01 metrge |
||||||
sozıw |
ushın |
10N |
kúsh kerek ekenligi málim. Bunda k prujnanıń qattılıǵına |
|||||
baylanısli proporcionallıq koefficient. Prujinanı 0,05 metrge sozıw ushın isleniwi kerek bolǵan jumıstı esaplań. (J. 0,125 kgm).
MENSHIKSIZ INTEGRALLAR
§1. Menshiksiz inyegrallardıń qásiyetleri hám esaplaw usılları
b |
|
|
Eskertiw. f x dx túrindegi menshiksiz |
integrallar qarastırıladı. f x |
|
a |
|
|
funkciya a;b kesindisinde úzliksiz. Bunda a |
shekli noqat, b shekli noqat |
|
yamasa hám a;b ushın |
f x funkciyasınıń a; segmetinde |
|
anıq integralı anıqlanǵan bolsın.
Anıq integral túsinigin integrallıq qosındılar shegi retinde anıqlaǵanda integrallaw kesindisi shekli hám bul kesindide integral astındaǵı funkciya shegaralanǵan funkciya bolıwı zárúr edi. Usı eki shártlerden keminde birewi orınlanbasa, onda anıq integraldıń integrallıq qosındılar shegi retindegi anıqlaması maǵanaǵa iye bolmaydı.
Usıǵan baylanıslı anıq integral túsinigin ulıwmalastırıw máselesi kelip shıǵadı. Solardan biri bolǵan menshiksiz integrallar túsinigin qarastıramız.
1 . Integrallaw shekleri sheksizlik bolǵan menshiksiz integrallar.
|
1 -anıqlama. Meyli |
f (x) |
funkstiya a x kesindide úzliksiz bolsın. |
||
Onda |
bul |
funkstiya |
a |
||
teńsizligin |
qanaatlandıratuǵın |
|
|||
|
|||||
ushın |
hár |
bir |
a, segmentinde |
||
úzliksiz funkciya boladı hám bunnan
f (x)dx
a
11- suwret
integralınıń bar bolıwı kelip shıǵadı. Bul integral óziniń joqarǵı shegi bolǵan ge
|
|
|
|
baylanıslı hám |
a kesindide anıqlanǵan funkciya boladı. Eger |
f (x)dx |
|
|
|
|
a |
|
|
|
|
integralınıń shekli shegi bar bolsa, onda bul shekti |
|
|
|
f (x)dx |
túrinde |
||
|
|
a |
|
belgileydi hám |
f (x) funkciyasınıń ( a dan ke shekemgi) sheksiz kesindi |
||
|
|
|
|
boyınsha menshiksiz integralı dep delinedi. Bul jaǵdayda |
f (x)dx menshiksiz |
||
|
a |
|
|
integralı jıynaqlı dep ataladı.

|
|
Eger da |
f (x)dx integralınıń shegi bar bolmasa yamasa bul |
|
a |
|
|
integraldıń shegi sheksizlik bolsa, onda f (x)dx simvolı hesh bir sanlı mánis
a
penen baylanıstırılmaydı. Usı jaǵdayda da f (x)dx integralına menshiksiz
a
integral delinedi, biraq bul jaǵdayda menshiksiz integraldı tarqalıwshı dep aytamız. Solay etip
|
|
f (x)dx lim |
|
|
|
|
|
|
f (x)dx . |
|
|||
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
Usıǵan uqsas x b |
sheksiz kesindide uzliksiz |
f (x) funkciyasınıń |
||||
b |
|
b |
f (x)dx lim |
b |
|
|
|
f (x)dx menshiksiz integralı |
f (x)dx |
turinde anıqlanadı hám |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Barlıq haqıqıy sanlar kósherinde úzliksiz f x funkciya úshın |
|
f (x)dx |
|
|
|
|
|
a |
|
|
menshiksiz integralı |
f x dx |
|
f x dx |
|
|
|
|
|
a |
|
a |
|
|
|
Bunda a qálegen háqıqıy san. |
f x dx |
hám |
||
|
|
|
|
|
|
|
|
|
|
f x dx teńligi menen anıqlanadı.
f x dx menshiksiz integralları
a
jıynaqlı bolsa, |
onda |
f x dx menshiksiz integralı jıynaqlı delinedi, eger |
||
|
|
|
|
|
|
|
|
|
|
f x dx |
|
|
f x dx menshiksiz integrallarınıń keminde birewi tarqalıwshı |
|
hám |
|
|||
|
|
a |
|
|
|
|
|
|
|
bolsa, onda |
f x dx |
menshiksiz integralı tarqalıwshı dep ataladı. |
||
|
|
|
|
|
Bul keltirilgen jıynaqlı menshiksiz integrallardıń anıqlamalarınan menshiksiz integrallar integrallıq qosındılardıń shegi emes, al joqarı yamasa tómengi shegi ózgeriwshi bolǵan anıq integrallardıń bul shekler sheksizlikke úmtılǵandaǵı shegi ekenligin atap ótemiz.
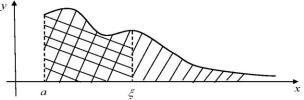
Geometriyalıq kózqarastan f x dx integralınıń sanlı mánisi x a , x
a
tuwrıları menen oń hám shep tárepten shegaralanǵan, tómennen ox kósheriniń
a, kesindisi menen hám joqarıdan y f x funkciyasiniń grafigi menen shegaralanǵan iymek sızıqlı trapeciyanıń maydanına teń bolıwı málim. Bunda
y f x |
funkciya |
a, |
yarım |
tuwrıda úzliksiz |
hám teris emes. |
Eger |
|
|
|
|
|
|
|
f x dx |
menshiksiz integralı jıynaqlı bolsa, onda onıń mánisin tómennen |
ox |
||||
a |
|
|
|
|
|
|
kósheri, shep tárepten |
x a |
tuwrısı |
hám joqarıdaǵı |
y f x funkciyasınıń |
||
grafigi menen shegaralanǵan 11-súwrettegi shtrixlanǵan figuranıń maydanı retinde qabıl etedi. Usıǵan uqsas geometriyalıq maǵananı
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
x dx |
hám f x dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
integralları úshın da keltiriw múmkin. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
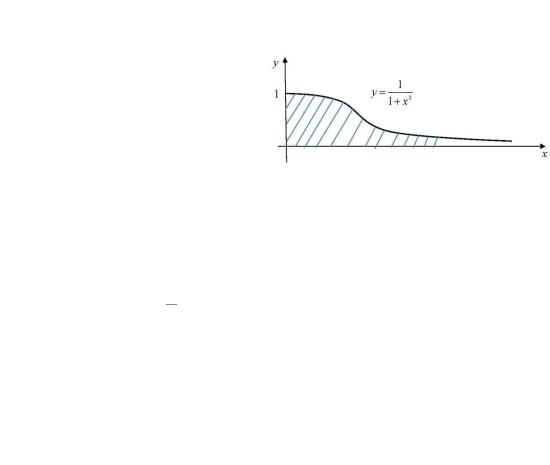
1-mısal. |
|
|
|
|
|
|
menshiksiz |
|
integralın |
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
0 |
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
jıynaqlılıqqa izertleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12- suwret |
|
|||
Sheshiliwi: 0 úshın |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
arctgx |
|
|
arctg hám |
lim arctg |
|
bolǵanı ushın berilgen integral |
|||||||||||||||
2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
jıynaqlı |
|
hám onıń mánisi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
ge teń, yaǵnıy 0 1 x2 |
|
2 . |
Geometriyalıq |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ge teń. |
|
|
|
|
|
||||||
kózqarastan shtrixlanǵan figuranıń maydanı |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 -mısal. cos xdx menshiksiz integralın jıynaqlılıqqa izertleń. |
|
|
|
|||||||||||||||||||||
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
sin |
|
lim sin |
||||||
|
|
|
|
|
|
|
|
cos xdx sin x |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Sheshiliwi: |
|
|
|
|
|
ushın |
|
|
|
0 |
|
|
|
hám |
|
shegi bar |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0
bolmaǵanlıǵı ushın berilgen menshiksiz integral tarqalıwshı.
1
3 -mısal. 2xdx integralın jıynaqlılıqqa izertleń.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Bunnan |
|||||||||||||
Sheshiliwi: |
|
|
|
|
|
|
|
|
|
|
|
úshın |
segmetinde |
|
|
2 dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,1 |
|
|
|
|
|
|
|
|
|
|
|
|
ln 2 ln 2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 . |
|||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
bolǵanı ushın berilgen integral jıynaqlı hám |
2x dx |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln 2 |
|
||
|
ln |
|
ln |
|
|
|
|
|
ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4 -mısal. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
integralın jıynaqlılıqqa izertleń. Bunda |
|
|
|
-bazıbir háqıqıy san. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 , |
|
eger 1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Sheshiliwi: 1; ushın |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
eger 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
1 |
, |
|
eger 1 ln , |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
bolǵanlıqtan |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
. |
Demek, |
|
|
|
menshiksiz integralı |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
eger |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 mánislerinde jıynaqlı hám 1 mánislerinde tarqalıwshı boladı. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5 -mısal. |
|
|
|
|
|
|
|
|
|
|
|
|
integralınıń |
jıynaqlı bolıwın kórsetiń hám onıń mánisin |
||||||||||||||||||||||||||||||||||||||||||||||||||||
1 x x2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tabiń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Sheshiliwi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, R |
|
|
|
|
|
|
hám |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ushın |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg 2 1 arctg |
2 1 |
||||||||||||||||||||||||||
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2x 1 |
|
|
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 x |
x |
|
|
|
3 |
|
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
boladı. Endi |
|
|
lim arctg |
|
|
|
|
|
|
|
; |
lim arctg |
|
|
|
|
|
|
|
|
bolǵanı ushın |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, yaǵnıy berilgen integral jıynaqlı hám |
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x x |
2 |
|
|
3 |
|
||||||||||
1 x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Eskertiw. |
|
|
|
|
f x dx |
menshiksiz |
|
|
integralınıń |
|
jıynaqlılıǵı |
|
f x dx |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
||
menshiksiz integralınıń jıynaqlılıǵı menen teń kúshli boladı. Bunda |
c a; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
qálegen san. Sebebi a c teńsizligin qanaatlandıratuǵın ushın |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x dx f x dx f x dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
teńligi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
§2. Sheksiz kesindiler boyınsha menshiksiz integrallardıń qásiyetleri |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 . |
Eger |
|
|
|
|
f (x) |
|
|
|
|
|
hám g(x) |
|
funkciyalarınıń a; kesindisi |
boyınsha |
||||||||||||||||||||||||||||||||||||||||||||||||
menshiksiz |
|
|
|
integralları |
|
|
jıynaqlı |
bolsa, |
|
|
|
onda |
|
|
|
, R |
|
|
|
sanlarında |
||||||||||||||||||||||||||||||||||||||||||||||

|
f |
|
x |
|
g |
|
x |
funkciyasınıń |
|
|
a; |
kesindi boyınsha menshiksiz integralı da |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
jıynaqlı hám |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
f x g x dx f x dx g x dx |
|
|
||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
a |
|
|
|
teńligi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Dálillew: a; ushın anıq integraldıń sızıqlılıq qásiyeti tiykarında |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x g x dx f x dx g x dx |
|
|
||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
a |
|
|
|
boladı. Bul teńliktiń oń tárepi |
|
shekli shekke iye, sebebi |
f (x) hám |
|||||||||||||||||
g(x) |
funkciyalarınıń a; kesindisi boyınsha menshiksiz integralları jıynaqlı. |
|||||||||||||||||||
Onda bul teńliktiń shep tárepiniń de |
shekli shegi bar hám |
1 |
teńligi |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Dálillengen qásiyet |
|
;a |
|
hám |
|
; |
kesindileri boyınsha alınǵan |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f (x) |
hám |
|
g(x) funkciyalarınıń |
menshiksiz |
integralları |
jıynaqlı |
bolǵan |
|||||||||||||
jaǵdaylar ushında orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 . Eger |
F x funkciyası |
a; kesindisinde úzliksiz |
f (x) |
tıń |
a, |
|||||||||||
kesindisindegi |
|
baslanǵısh funkciyası |
|
bolsa, |
onda a |
shártin |
||||||||||||||
qanaatlandıratuǵın ushın |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( ) F (a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
f (x)dx F (x) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
Nyuton-Leybnic formulası orınlı. Demek, f (x)dx menshiksiz integralı jıynaqlı
a
bolıwı ushın
Eger lim F ( )
shekli sheginiń bar bolıwı zárur hám jeterli boladı. shekli shegi bar bolsa, onda
|
f (x)dx lim F ( ) F (a) |
|
|
a |
|
|
boladı. lim F ( ) F ( ) |
belgilewin kiritip |
|
|
|
|
|
|
|
|
||
|
|
|
f (x)dx F ( ) F (a) F (x) |
|
|
a |
|
a |
|
||
teńligine iye bolamız. Usı teńlik ulıwmalasqan Nyuton-Leybnic formulası dep ataladı. Usıǵan uqsas sáykes shártler orınlı bolǵanda

a |
a |
|
|
|
|
|
f (x)dx F(a) F( ) F(x) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f (x)dx F ( ) F ( ) F (x) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
túrindegi ulıwmalasqan Nyuton-Leybnic formulaların alıw múmkin. |
|
|
|
|
|||||||||||||||
|
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1- mısal. |
|
dx integralın esaplań. |
|
|
|
|
|
|
|
|
|
|||||||
|
1 x2 |
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
0 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||
arctgx |
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|||||||
|
|
dx arctgxd(arctgx) |
|
|
arctg |
x |
|
|
|
|
(arctg |
( ) arctg |
0) |
|
|
. |
|||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
1 x2 |
0 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
8 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3.Bóleklep integrallaw. Meyli u x , v x funkciyaları [a; ) kesindisinde |
||||||||||||||||||
anıqlanǵan, a; segmentte úzliksiz tuwındılarına iye. Bunda a; . Eger
lim u v u v shekli shegi bar, |
|
|
||||||||||||
|
menshiksiz integralı |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
vu dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jıynaqlı bolsa, onda |
|
menshiksiz integralı da jıynaqlı hám |
||||||||||||
|
uv dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uv dx |
uv |
|
0 vu |
dx |
|
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
bóleklep integrallaw formulası orınlı. |
|
|
|
|
|
|
a; segmentte úzliksiz bolǵanı |
|||||||
Haqıyqatında da u x , v x funkciyaları |
||||||||||||||
ushın a; mánisinde |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
uv dx |
uv |
|
0 |
|
vu dx |
|
|
|||||
|
|
|
|
|
|
|||||||||
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
anıq integral ushın bóleklep integrallaw formulası orınlı. Onda
|
|
|
|
|
|
|
|
|
|
dx u |
|
|
|
|
|
uv |
v u a v a vu dx |
|
|
||||
a |
|
|
|
|
a |
|
|
hám bul teńliktiń oń tárepi |
|
shekli shekke iye. Bul shek |
|
||||
|
|
uv |0 |
|||||
|
|
|
|
|
|
||
teń bolǵanı ushın, lim |
|
|
|
shekli shegi bar, yaǵnıy |
|
uv dx |
|
|
uv dx |
|
|
|
|||
a |
|
|
|
a |
|
||
integral jıynaqlı hám bóleklep integrallaw formulası orınlı.
vu dx qa
a
menshiksiz
Mısal. xe xdx menshiksiz integraldı esaplań.
0 |
|
|
|
Sheshiliwi: xe |
|
dx xe |
|
| 0 |
e |
x |
x |
| |
|
1 . |
x |
x |
dx e |
|
0 |
||||||
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
§3. Shegaralanbaǵan funkciyalardıń |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
menshiksiz integralları |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
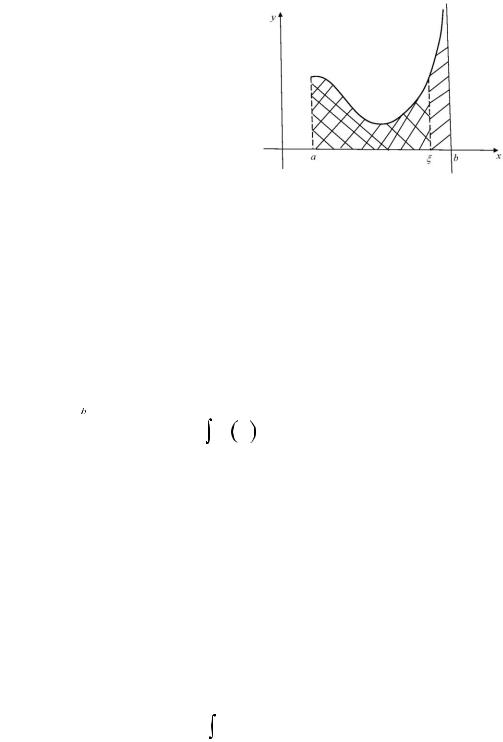
Meyli |
f |
x |
funkciya |
a;b |
|
yarım |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
segmentte |
úzliksiz, |
bıraq |
|
x b |
|
|
noqattıń |
|
|
|
|
|
|
||||||||
|
dógereginde |
shegaralanbaǵan |
bolsın. |
|
Onda |
|
|
|
|
|
|
|||||||||||
|
|
|
|
a;b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x funkciya |
te úzliksiz bolǵanı ushın |
|
|
|
|
|
|
||||||||||||||
|
hárbir |
a; a;b te |
integrallanıwshı |
hám |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13- suwret |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x dx |
integral |
óziniń |
joqarǵı sheginiń a b kesindisinde |
anıqlanǵan |
|||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
funkciyası boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eger |
limb 0 |
f x dx |
shekli shegi |
|
bar bolsa, onda bul shekti |
|
f x dx |
||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
túrinde |
belgileymiz |
hám |
|
shegaralanbaǵan |
funkciyanıń |
|
|
ti boyınsha |
|||||||||||||
|
|
a;b |
|
|||||||||||||||||||
|
menshiksiz integralı dep ataymız, yaǵnıy |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
f x dx lim |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
f |
x |
dx . |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
b 0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
Bul teńliktiń |
oń tárepindegi |
shek |
bar |
bolsa |
hám |
shekli |
bolsa, onda |
||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx menshiksiz integralı jıynaqlı delinedi, al eger teńliktiń oń tárepindegi |
|||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
shek bar bolmasa yamasa sheksizlik bolsa onda |
f (x)dx |
menshiksiz integralı |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
tarqalıwshı |
dep |
ataladı. Usıǵan |
uqsas |
|
a,b yarım |
intervalda |
uzliksiz, bıraq |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
x a |
noqat dógereginde |
|
shegaralanbaǵan |
f (x) |
funkciya ushın |
f (x)dx |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
menshiksiz integral túsinigi kiritiledi hám ol |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
lim |
f (x)dx |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
a 0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
teńligi |
menen anıqlanadı. Eger bul |
teliktiń oń tárepindegi shek bar hám shekli |
|||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bolsa, |
onda f (x)dx |
menshiksiz |
|
|
integralı |
|
jıynaqlı, al |
eger |
teńliktiń oń |
||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
tárepindegi shek bar bolmasa yamasa sheksizlik bolsa, onda f (x)dx |
|
menshiksiz |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a, x b |
|||||
|
integralı tarqalıwshı |
dep |
ataladı. |
a,b |
|
|
intervalda úzliksiz |
hám |
||||||||||||||
|
noqatlarınıń dógereginde shegaralanbaǵan |
|
f (x) |
funkciyanıń menshiksiz integralı |
||||||||||||||||||

|
|
|
|
b |
|
c |
b |
|
|
|
|
|
|
|
|
f (x)dx f (x)dx f (x)dx |
|
|
|
||||
|
|
|
|
a |
|
a |
c |
|
|
|
|
teńligi menen anıqlanadı. Bunda c a,b |
qálegen noqat. Eger bul teńliktiń oń |
||||||||||
|
|
c |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tárepindegi |
f (x)dx |
hám |
f (x)dx menshiksiz integralları |
jıynaqlı bolsa, |
|||||||
|
|
a |
|
|
c |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
c |
|
|
b |
onda f (x)dx menshiksiz integralı jıynaqlı, al eger f (x)dx |
hám f (x)dx |
||||||||||
a |
|
|
|
|
|
|
|
a |
|
|
c |
|
|
|
|
|
|
|
|
|
b |
|
|
menshiksiz integrallardan keminde biri tarqalıwshı bolsa, |
f (x)dx |
menshiksiz |
|||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
integralı tarqalıwshı dep ataladı. |
|
|
|
|
|
|
|
||||
Meyli f(x) funkciya a,b segmentiniń |
x c noqatınan basqa noqatlarında |
||||||||||
uzliksiz |
al |
x c |
noqatınıń dógereginde shegaralanbaǵan bolsın. Bul jaǵdayda |
||||||||
b |
|
|
|
|
b |
c |
|
b |
|
|
|
f (x)dx |
menshiksiz integralı |
f (x)dx |
f (x)dx f (x)dx |
|
|
||||||
a |
|
|
|
|
a |
a |
|
c |
|
|
|
teńligi menen anıqlanadı |
hám |
bul |
teńliktiń oń |
tárepindegi hárbir |
menshiksiz |
||||||
|
|
|
|
|
|
|
|
b |
|
|
|
integral |
jıynaqlı |
bolsa, onda shep |
tárepindegi |
f (x)dx |
menshiksiz integralı |
||||||
|
|
|
|
|
|
|
|
a |
|
|
|
jıynaqlı boladı. Al, eger teńliktiń oń tárepindegi menshiksiz integrallardan keminde birewi tarqalıwshı bolsa, onda onıń shep tárepindegi menshiksiz integral da tarqalıwshı boladı.
|
f x funkciya shekli |
a;b |
intervalınıń shekli sandaǵı |
xk , k |
|
|
|||||||||
|
1,m |
||||||||||||||
noqatlarınan |
basqa |
noqatlarda |
anıqlanǵan jaǵdayda, |
a x0 x1 x2 |
|
xm b |
|||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
shárti |
orınlı |
dep |
esaplap |
f x dx |
menshiksiz |
|
|
integralın |
|||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
xk 1 ; xk , k 1, 2, |
|
intervalları |
boyınsha |
f x funkciyanıń |
menshiksiz |
||||||||||
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
integrallarınıń |
qosındısı |
retinde anıqlaymız. |
Eger |
f |
k 1,2, , m |
||||||||||
|
x dx, |
|
|
|
|
|
|||||||||
xk 1
menshiksiz integrallarınıń hárbiri jıynaqlı bolsa, onda berilgen menshiksiz integral
xk |
|
|
k 1,2, ,m |
menshiksiz integrallarınıń |
jıynaqlı boladı. Al, eger f |
|
x dx, |
|
keminde birewi tarqalıwshı bolsa, onda berilgen menshiksiz integral tarqalıwshı boladı.
Keltirilgen anıqlamalardan shegaralanbaìan funkciyalardıń shekli kesindisi boyınsha menshiksiz integralı integrallıq qosındınıń shegi emes, al
