
Aniq integrallar
.pdf
2-mısal. x a(t sint), y a(1 cost), 0 t 2 cikloydasınıń bir arkası
OX kósheriniń dógereginde aylanıwında payda bolǵan aylanba betliktiń maydanın tabıń.
Sheshiliwi. (S) formulasına sáykes, |
|
|
|
|
|
|
2 |
|
t |
|
64 |
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
P(L) 2 a |
2 |
(1 cost) |
(1 cost) |
2 |
sin |
2 |
tdt 8 a |
2 |
|
3 dt |
|
a2. |
||||
|
|
|
|
sin |
2 |
|
3 |
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3-mısal. r = 5(1 + sin q), 0 q teńlemesi |
menen |
berilgen |
iymek sızıǵı |
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
polyarlıq kosher dógereginde aylanıwında payda bolǵan betliktiń betiniń maydanın tabıń.
Sheshiliwi. (D) formulasına sáykes,
|
|
|
2 |
|
2 |
P 10 (1 sin )sin |
25(1 sin )2 |
25cos2 d 5 |
2 |
(1 sin )3 sin d |
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
3 |
|
|
|
|
54 |
2 76 |
|
|
|
|||
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
2 (sin |
|
cos |
|
) sin |
|
cos |
|
d |
|
|
. |
|
|
||
2 |
2 |
2 |
2 |
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
8-§. Anıq integraldıń fizikalıq qollanıwları |
|||||||||||||
1.Ózgeriwshi kúshtiń jumisı. Ózgeriwshi F(t) kúshiniń [a,b] segmentinde
b
islegen jumısı A F (t)dt formulası járdeminde tabıladı (1-§ tı qarań).
a
1-mısal. Sırtqı kúshlerdiń, massası m bolǵan deneni jerdiń betinen kosmostıń jer orayınan R ge teń qashıqlıqtaǵı noqatına shıǵarıw ushın, orınlawı zárúr bolǵan minimal jumısın esaplań.
Sheshiliwi. Máseleni sheshiw jolın apiwayılastırıw maqsetinde denege jerden basqa kosmos obektleri tásir etpeydi dep esaplaymız. Sonda massası m bolǵan
denege jer tárepinen dene menen jer orayı |
arasındaǵı r |
qashıqlıǵınan |
ǵárezli |
|||
bolǵan pútkil álemlik tartılıw kúshi |
F |
Mm |
tásir |
etedi. Bunda |
|
|
|
T |
|
r2 |
|
|
|
gravitaciyalıq turaqli, M jerdiń massası. Sonıń menen birge deneni jerdiń betinen kóteriw ushın oǵan FT kúshine qarama-qarsı baǵıtlanǵan sıtqı FS kúshi menen tásir etiliwi hám FS FT shárti orınlı bolıwı tiyis. Sonda minimal jumıs FS FT sheklik jaǵdayında islenedi. Onda jerdiń radiusın Rj , jer betinen dene ótkeriliwi
tiyisli bolǵan kosmos noqatına |
|
shekemgi |
qashıqlıqtı |
R arqalı belgilep, |
izlenip |
|
|||||||
atırǵan minimal jumıstıń A |
R |
F (r)dr |
R |
F (r)dr |
|
1 |
|
1 |
|
1 |
|
|
|
R |
|
|
|
, |
|||||||||
|
|
|
|
|
Mm |
|
dr Mm( |
|
|
|
) |
||
|
S |
T |
|
|
|
|
|
||||||
R |
|
R |
|
R |
r2 |
|
|
Rj |
R |
|
|||
|
j |
|
j |
|
j |
|
|
|
|
|
|
|
|

|
|
A Mm( |
1 |
|
|
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
yaǵnıy |
|
|
|
|
|
Rj |
R |
|
|
|
|
bolıwın |
kóremiz. |
Bunnan |
berilgen |
deneni |
jerdiń |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
betinen sheksiz uzaqlastırılǵan kosmos noqatına jiberiw ushın |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
A lim A Mm lim( |
1 |
|
|
|
1 |
) |
Mm |
|
jumısin islew talap etiliwin kóremiz. |
||||||||||||||||||||||
|
R |
|
|
|
|
R |
R |
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Materiallıq noqattıń qozǵalısına baylanıslı máseleler. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2-mısal. Materiallıq noqattıń OX |
kósherı boyınsha tuwrı sızıqlı qozǵalıs |
||||||||||||||||||||||||||||||
teńlemesi |
S S (t) , |
t [t |
0 |
|
,t ] |
túrinde berilgen bolsa, onda materiallıq noqattıń |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
háreketin |
kúzetiw waqıtıniń |
|
baslanǵısh |
t0 |
momentinen waqıttıń |
t1 |
momentine |
||||||||||||||||||||||||
shekemgi |
|
waqıt |
intervalinda |
ótken |
jolı |
S S(t1) S(t0) |
formulası |
menen |
|||||||||||||||||||||||
anıqlanadı. Eger |
materiallıq |
|
noqattıń tezliginiń waqittan ǵarezli boliw nızamı |
||||||||||||||||||||||||||||
v (t), t [t0,t1] |
málim |
|
bolsa, |
|
onıń |
waqıtıniń baslanǵısh t0 |
momentinen |
||||||||||||||||||||||||
t t1 momentine shekemgi waqıt intervalında basıp ótken jolın tabıń. |
|
|
|
||||||||||||||||||||||||||||
Sheshiliwi. |
Tuwrı |
|
sızıqlı |
|
qozǵalıstaǵı |
materiallıq |
noqattıń |
tezligi |
|||||||||||||||||||||||
v (t) |
dS (t) |
, |
|
t [t 0 ,t1] bolǵanı ushın, materiallıq noqattıń basıp ótken jolı |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S S(t) S(t0 ) |
|
ge |
teń |
|
boladı, eger háreket baǵıtı turaqlı bolsa. Ulıwma |
||||||||||||||||||||||||||
jaǵdayda |
materiallıq |
|
noqattıń |
OX |
|
kósherı |
boyınsha |
teń |
ólshewli bolmaǵan |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
||
qozǵalıstıńda háreket baǵıtı turaqlı |
bolmasa, onda ótilgen joldı, |
S |
|
|
(t) |
|
dt |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
||
formulası járdeminde esaplaydı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3-mısal(tuwrı sızıqlı emes qozǵalıs). Sırǵanamastan OX |
kósherı boyınsha |
|||||||||||||||||||||||||||||
domalap |
|
baratuǵın |
radiusı |
|
r |
ge |
teń |
dóńgelekte |
M |
noqatı |
belgilengen. |
||||||||||||||||||||
Dóńgelektiń bir tolıq aylanıwında M noqatı ótken jolın tabıń. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Sheshiliwi. Meyli waqittıń |
t 0 baslanǵısh momentinde M |
noqatı tómengi |
|||||||||||||||||||||||||||||
awhalında |
|
OXY |
|
|
koordinatalar |
|
sisteması |
basında |
bolsın. |
M |
noqatınıń |
||||||||||||||||||||
koordinataları menen burılıw múyeshi arasındaǵı ǵárezlilik, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
y r(1 cos ), |
x r( sin ), 0 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
túrinde jazıladı. Bul formulalar menen anıqlanatuǵın iymek sızıq cikloyda arkası
bolıwı málim. Al bizler izlep otırǵan jol usı arkanıń uzıliǵına teń, yaǵnıy |
||||||
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S |
d |
2r(1 cos )d 2r sin |
||||
2d 8r. |
||||||
0 |
0 |
0 |
|
|||
3. Materiallıq sızıqlar hám plastinkalardıń inerciyalıq hám statikalıq momentleri. 1. Materiallıq noqattıń radiusı r ge teń sheńber boyınsha teń
ólshewli qozǵalısındaǵı múyeshlik tezligi menen v sızıqlı tezligi v r

teńligi arqalı baylanısadı. Tegislikte |
massası m bolǵan A materiallıq noqatı |
berilgen bolsın. Bul noqat bazıbir l |
kósheriniń dógereginde orayı O l noqatıda |
bolǵan, radiusı r ge teń sheńber boyınsha aylanǵanda onıń kinetikalıq energiyası
E |
mv2 |
|
|
mr2 2 |
túrinde ańlatıladı. Eger A materiallıq noqatınıń bunday aylanba |
||||||
|
|
|
|||||||||
2 |
2 |
|
|
|
|
|
|
||||
qozǵalısın xarakterleytuǵın |
I mr 2 shamasın kiritsek, onda kinetikalıq energiya |
||||||||||
E |
I 2 |
|
túrindegi ápiwayı kórinisine iye boladı. Usı kiritilgen |
I mr2 |
shamasına |
||||||
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
||
A materiallıq noqatınıń l |
|
kósherine (O noqatına) baylanıslı inerciyalıq momenti |
|||||||||
dep ataladı. A |
materiallıq noqatınıń l |
kósherine baylanıslı statikalıq momenti |
|||||||||
dep A noqatı menen l |
kósherine shekemgi qashıqliqtıń d |
shaması menen A |
|||||||||
noqatına jaylastırılǵan massanıń kóbeymesine aytıladı hám Ml |
arqalı belgilenedi, |
||||||||||
yaǵnıy |
|
Ml md . Eger |
tegislikte |
OXY dekart koordinatalar |
sisteması |
||||||
belgilengen hám |
A(x, y) |
noqatına m massası jaylastırılǵan bolsa, onda A(x, y) |
|||||||||
materiallıq noqatınıń koordinata kósherlerine hám koordinata basına baylanıslı
inerciyalıq |
momentleri |
sáykes |
|
|
túrde |
IOX |
my2 , |
IOY |
mx2 |
hám |
||||||||||||||||||
I |
O |
m(x2 y2 ) ,al koordinata kósherlerine baylanıslı statikalıq momenleri sáykes |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
túrde MOX |
my, |
MOY mx |
formulaları járdeminde tabıladı. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2. Eger massaları sáykes |
mk , k 1,n |
bolǵan n |
materiallıq noqatlar sistemasın |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
radiusları sáykes |
rk , k 1, n |
bolǵan sheńberler boyınsha belgilengen |
l kosheri |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dógereginde turaqlı |
múyeshlik tezliginde aylandırılsa, onda bunday qozǵalıstaǵı |
|||||||||||||||||||||||||||
noqatlar sistemasınıń qosındı kinetikalıq energiyası |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
m v2 |
n m |
2r2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
E |
|
k |
k |
|
|
|
k |
|
k |
|
|
|
|
|
(1) |
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
|
|
|
|
|
|
|
|
|||||||
túrinde jazıladı. |
|
Eger |
noqatlar |
sistemasınıń |
bunday |
aylanba |
qozǵalısın |
|||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xarakterlewshi I m r2 |
shaması kiritilse, onda qosındı kinetikalıq energiyanı |
|||||||||||||||||||||||||||
|
|
E I 2 |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ápiwayı |
|
|
túrinde |
jazıw |
múmkin. Usı |
kiritilgen |
|
|
shamasına |
|||||||||||||||||||
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
materiallıq |
noqatlar |
sistemasınıń |
berilgen |
l |
kósherine |
baylanıslı |
inerciyalıq |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
momenti dep ataydı. Demek, massaları sáykes |
|
mk , k 1,n |
|
bolǵan |
Ak , k 1, n |
|
||||||||||||||||||||||
materiallıq noqatlar sistemasınıń belgilengen l |
|
kósherine |
baylanıslı |
inerciyalıq |
||||||||||||||||||||||||
momenti bul sistemaǵa kiritilgen hárbir noqattıń usı |
l |
|
kósherine |
baylanıslı |
||||||||||||||||||||||||
inerciyalıq momentleriniń qosıdısına teń boladı. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
mk , k 1, n |
|
|
|
|
|
|
|
|
||||||||||
Massaları |
sáykes |
|
bolǵan |
Ak , k 1, n |
|
|
materiallıq |
noqatlar |
|||||||||||||||
sistemasınıń belgilengen |
l |
kósherine baylanıslı |
statikalıq momenti |
|
dep usı |
||||||||||||||||||
noqatlardıń hár birinen |
l |
kósherine baylanıslı statikalıq momentleri qosındısına |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
aytamız. Bunday Ak , k 1,n |
materiallıq noqatları |
sisteması berilgen jaǵdayda |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
mk , k 1,n |
|
massaları |
awırlıq |
orayı |
dep |
atalatuǵın |
C(xC , yC ) |
|
noqatına |
||||||||||||||
jámlenedi. Usı |
|
C(xC , yC ) |
awırlıq |
orayınıń l kósherine |
baylanıslı |
statikalıq |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
momenti |
Ak , k |
1,n |
|
materiallıq |
|
noqatlar sistemasınıń |
l |
kósherine |
baylanıslı |
||||||||||||||
statikalıq momentine teń boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Eger tegislikte |
OXY |
dekart koordinatalar sisteması belgilengen bolsa, onda |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
joqarıda |
keltirilgen |
anıqlamalarǵa |
|
sáykes |
massaları sáykes |
mk , k 1,n |
bolǵan |
||||||||||||||||
|
|
|
|||||||||||||
Ak (xk , yk ), k 1, n |
materiallıq noqatlar sistemasınıń koordinata kósherlerine hám |
||||||||||||||
koordinata basına baylanıslı inerciyalıq momentleri sáykes túrde |
|
||||||||||||||
I |
|
|
n |
m y |
2 |
, |
I |
n |
|
hám |
I |
|
m (x2 y2 ) |
||
|
|
|
2 |
|
|
|
|
||||||||
OX |
|
|
k k |
|
OY |
m k xk |
|
O |
|
k k |
k |
||||
|
|
k 1 |
|
|
|
|
|
k 1 |
|
|
|
|
k 1 |
|
|
formulaları járdeminde, al statikalıq momentleri bolsa, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
mk xk |
|
|
|
|
|
|
|
|
|
|
|
MOX mk yk , MOY |
|
|
|||||
|
|
|
|
|
|
|
|
|
k 1 |
|
|
k 1 |
|
|
|
formulaları járdeminde tabıladı. Materiallıq noqattıń statikalıq momenti hám materiallıq noqatlar sistemasınıń awırlıq orayınıń anıqlamalarına sáykes
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
MOX mk yk myC M XC , MOY mk xk mxC MYC , |
m mk |
|||||||||||||||||||||
k 1 |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
|||
teńlikleri |
orınlı. |
Bunda |
M XC , |
MYC |
awırlıq |
|
|
orayınıń sáykes OX , OY |
||||||||||||||
kósherlerine |
baylanısli |
statikalıq |
momentleri. |
Bunnan |
C(xC , yC ) |
awırlıq |
||||||||||||||||
orayınıń koordinataları ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
mk yk , |
|
|
|
|
||
|
|
|
|
M |
|
|
mk xk , |
, |
yC |
MOX |
|
|
|
|
|
|||||||
|
|
|
x |
|
|
k 1 |
|
k 1 |
|
|
|
|
|
|
||||||||
|
|
|
OY |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||||
|
|
|
c |
m |
|
|
|
|
|
m |
|
|
|
mk |
|
|
|
|
||||
|
|
|
|
|
mk |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
formulalarına iye bolamız. |
|
|
|
y f (x), |
|
|
a x b |
|
|
|
|
|||||||||||
3. Meyli L materiallıq iymegi |
|
|
teńlemesi |
menen |
||||||||||||||||||
berilgen |
bolsın. |
Bunda |
f (x) |
|
funkciyası |
|
|
[a,b] |
segmentinde |
úzliksiz |
||||||||||||
differenciallanıwshı funkciya. Eger |
L |
iymegine |
|
|
bólistirilgen |
massanıń |
sızıqlı |
|||||||||||||||
tıǵızlıǵı birge teń dep esaplasaq, onda |
L materiallıq |
iymeginiń massası usı |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
iymektiń S (L) |
uzınlıǵına teń boladı. Endi [a,b] segmentin T {xk , k |
0, n} |
||||||||||||||||||||
maydalaymız, |
(T ) bul maydalawdıń maydalıǵı bolsın. Sonda [a,b] segmentiniń |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
bul maydalanıwına L |
iymeginiń |
T {L , k 1, n} maydalanıwı sáykes keledi. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
L |
|
k |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Lk {y f (x), xk 1 |
x xk } , |
|
|
|
xk |
|
|
|
|
|
|
|
|
|
||||||||
|
|
hám S(Lk ) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Bunda |
|
|
|
|
|
2 |
dx , |
k 0, n . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ( f (x)) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk 1 |
|
|
|
|
|
|
|
|
|
|
|
(T ) |
|
|
|
|||||||||||||||||||||||
Bunnan |
T {xk , k |
0, n |
} maydawınıń |
maydalıǵı |
|
jeterli kishi bolǵanda |
||||||||||||||||||||||
S(L ) m |
|
|
1 ( f (x ))2 x |
, k 0,n boladı. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
k |
|
|
k |
|
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eger |
(T ) 0 da |
S (L ) 0 sa, |
onda |
L |
iymeginiń |
hárbir L |
bólegin |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
A |
k |
(x |
k |
, f (x |
k |
)) |
túrindegi materiallıq noqat dep qabıl etiw múmkin. Sonlıqtan L |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||||
iymeginiń |
|
OX |
hám |
OY |
kósherlerine hám |
koordinata |
|
basına baylanıslı |
||||||||||||||||||||
inerciyalıq momentlerin sáykes |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
I k |
|
m ( f (x ))2 ( f (x ))2 |
1 ( f (x ))2 x , I k |
|
m x x2 |
1 ( f (x ))2 x , |
||||||||||||||||||||||
OX |
|
|
|
k |
|
|
k |
|
|
k |
|
k |
k |
OY |
k k |
|
k |
|
|
|
k |
|
k |
|||||
I |
|
|
m (x2 |
( f (x ))2 ) |
túrlerinde hám OX |
hám OY |
|
kósherlerine baylanıslı |
||||||||||||||||||||
O |
|
|
|
|
k |
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
statikalıq momentlerin sáykes |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Mk |
|
f (x )m f (x ) 1 ( f (x ))2 x , Mk |
|
x m x |
1 ( f (x ))2 x |
|
|
|
|
||||||||||||||||||||||||||
|
|
OX |
|
|
|
|
k |
|
k |
k |
k |
|
k |
|
OY |
|
k k |
k |
|
|
|
|
|
k |
k |
|
|||||||||
túrlerinde |
|
ańlatıw múmkin. Sonda |
|
L |
iymeginiń |
koordinata |
kósherlerine hám |
||||||||||||||||||||||||||||
koordinata basına baylanıslı inerciyalıq momentleri, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
I |
OX |
|
|
I k |
|
|
( f (x ))2 1 ( f (x ))2 x , I |
OY |
|
|
I k |
|
|
x2 1 ( f |
(x ))2 x , |
|
|||||||||||||||||||
|
|
X |
|
|
k |
k |
|
k |
|
Y |
|
k |
|
|
|
|
|
k |
k |
|
|||||||||||||||
|
|
|
|
k 1 |
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I (x2 ( f (x ))2) 1 ( f (x ))2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
O |
|
|
|
|
|
k |
|
|
|
|
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
al koordinata kósherlerine baylanıslı statikalıq momentleri bolsa, |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
M |
OX |
|
|
I k |
|
|
f (x ) 1 ( f |
(x ))2 x , M |
OY |
|
|
I k |
|
x |
k |
1 ( f (x ))2 |
x |
k |
|||||||||||||||||
|
|
|
|
X |
|
k |
k |
|
k |
|
|
|
Y |
|
|
|
|
k |
|
|
|||||||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
boladı. |
|
f (x) funkciyası [a,b] segmentide úzliksiz differenciallanıwshi bolǵanı |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ushın |
f (x) 1 ( f (x))2 , x |
1 ( |
|||||
funkciyaları |
usı |
segmentte úzliksiz |
|||||
Onda joqarıdaǵı |
juwıq teńliklerinde |
||||||
iymektiń OX , OY |
kósherlerine |
hám |
|||||
momentleri, |
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
f (x))2 , ( f (x))2 |
1 ( f (x))2 , x2 |
1 ( f |
|||
hám sonıń ushın integrallanıwshi boladı.
(T ) 0 da shekke otip, materiallıq koordinata basına baylanıslı inerciyalıq
b
IOX f 2(x) |
1 ( f (x))2 dx, |
IOY x2 1 ( f (x))2 dx , |
IO (x2 f 2 (x)) 1 ( f (x))2 )dx |
||||||||
a |
|
a |
|
|
|
a |
|
|
|
||
formulalarına hám OX , OY kósherlerine baylanıslı statikalıq momentleri |
|||||||||||
|
b |
|
|
|
|
|
b |
|
|
|
|
|
MOX |
f (x) 1 ( f (x)) |
2 |
dx, |
|
|
2 |
dx |
|||
|
|
MOY x 1 ( f (x)) |
|
||||||||
|
a |
|
|
|
|
|
a |
|
|
|
|
formulalarına sáykes anıqlanıwı múmkinligin kóremiz. Endi L materiallıq iymeginiń C(xC , yC ) massalar orayınıń koordinataların tabıw ushın

|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|||
MOX |
|
|
|
|
|
|
|
|
|
|
|
C M XC , MOY x |
|
|
|
|
|
C MYC |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||||
teńliklerinen paydalanıp, |
m S (L) |
bolǵanı ushın, |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 1 |
|
( f (x))2 dx |
|
|
|
|||||
xC |
M |
|
a |
|
|
|
|
M |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
OY |
|
|
|
|
|
, y OX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
b |
|
|
|
|
|
b |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||||||
formulalarına iye bolamız. Bul formulalardan ekinshisin |
2 ge kóbeytip, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
C b |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 y |
|
1 ( f (x))2 dx 2 |
f (x) 1 ( f (x))2 dx |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
túrinde jazsaq, 1 ( f (x))2 dx S(L) |
|
teńligi |
L {y f (x), a x b} iymeginiń |
||||||||||||||||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
uzınlıǵı, al 2 f (x) 1 ( f (x))2 dx P(L) |
|
|
formulası |
bolsa |
usı |
L iymegi OX |
|||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
kosheri dógereginde aylanǵanda payda bolǵan betliktiń betiniń |
P(L) maydanın |
||||||||||||||||||||||||||||||
tabıw formulası ekenligin esapqa alsaq, |
2 yCS(L) P(L) |
teńligine iye bolamız. |
|||||||||||||||||||||||||||||
Bul teńlik L iymegi ózi menen kesilispeytuǵın, biraq bir tegislikte jatıwshı kosher dógereginde aylanǵanda payda bolǵan betliktiń betiniń maydanı bul aylanıwdaǵı L iymeginiń massalar orayı sızgan sheńberdıń uzınlıǵın hám L iymeginiń óziniń
S (L) uzınlıǵınıń kóbeymesine teń degen maǵana beredi. Usi natiyje mexanikada
Guldenniń birinshi teoreması dep ataladı.
1-mısal. Uzınliǵı d ǵa teń bolǵan birtekli sterjenniń ortasına baylanıslı inerciya momentin, statikalıq momentin hám massalar orayınıń koordinataların tabıń.
Sheshiliwi. Sterjenniń ortasına baylanıslı inerciya momenti degende onıń qaq ortası arqalı ótetuǵın hám sterjenge perpendikulyar bolǵan qálegen kósherge baylanıslı inerciya momenti túsiniledi. Bizler sterjendi qaq ortası koordinata
basında bolatuǵınday etip OX kósheriniń |
|
d |
x |
d |
kesindisine jaylastıramız. |
|
|
||||
|
2 |
2 |
|
||
Sonda sterjenniń ortasına baylanıslı inerciya momentin esaplaw ushın onıń OY kósherine baylanıslı inerciya momentin esaplaw jeterli boladı, yaǵnıy
d
2
IOY d x2 
|
|
|
2 |
Endi |
m |
bolǵanı ushın |
|
|
d |
||
|
|
|
|
|
|
|
|
|
|
|
|
d |
dx |
|
f (x) 0, x [ |
d |
, d ] |
|
2 |
||
|
|
|||||||
|
|
|||||||
|
|
|
|
2 2 |
|
d |
||
|
|
|
|
|
|
|
2 |
|
|
md 2 |
|
|
|
|
|
||
IOY |
|
|
|
boladı. |
|
|
||
12 |
|
|
||||||
|
|
|
|
|
|
|||
x2dx d 3 . 12

Bunda m sterjenniń massası. f (x) 0, x [ |
d |
|
|
d |
] bolǵanı ushın |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
d |
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 f 2(x) |
1 |
|
|
|
2 |
0dx 0, |
IO IOX |
IOY IOY .Statikalıq momentleri: |
||||||||||||||||||||||||||||
IOX |
( f (x))2 dx |
||||||||||||||||||||||||||||||||||||
|
d |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
f (x) 1 ( f (x))2 dx 0 , |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
MOX |
MOY |
x 1 ( f |
|
|
dx |
|
|
|
|
||||||||||||||||||||||||||||
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
d |
|
|
|
|
|
|
|
|
C |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|d 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
xdx |
|
|
|
|
0. Awırlıq orayı |
x |
y |
0 boladı. |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
d |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Meyli |
G {(x, y) : a x b, 0 y f (x)} |
|
|
iymek sızıqlı trapeciyası berilgen |
||||||||||||||||||||||||||||||||
bolsın. |
Bunda |
|
f (x) |
funkciyası |
[a,b] segmentinde |
úzliksiz |
funkciya. G |
||||||||||||||||||||||||||||||
trapeciyasina |
|
m massa |
ǵa teń tıǵızlıqta bolistirildi. Kelip shıqqan materiallıq |
||||||||||||||||||||||||||||||||||
trapeciyasınıń |
|
OY kósherine baylanıslı inerciyalıq momentin esaplaw máselesin |
|||||||||||||||||||||||||||||||||||
qarastıramız. |
|
|
[a,b] |
segmentin |
T {x |
a |
b a |
|
|
k, k 0,n} usılında maydalap, |
|||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
{ k , k 1, n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
}, |
k k [xk 1, xk ], k 1, n |
, |
|
|
tańlawın júzege asıramız. Sonda |
||||||||||||||||||||||||||||||||
[a,b] segmentiniń |
T |
usılında maydalanıw |
|
|
|
usılına |
materiallıq trapeciyanıń |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Gk {(x, y) : xk 1 x xk , 0 y f (x)}, k 1,n |
|
|
maydalanıwı |
sáykes |
|||||||||||||||||||||||||||||||||
keledi. T maydalawınıń (T ) maydalıǵı |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
jeterli |
kishi bolsa, |
Gk , k 1, n |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
trapeciyaları |
|
|
ultanı |
|
biyikligi |
f (xk ) , k 1, n |
teń bolǵan jińishke |
||||||||||||||||||||||||||||||
tuwrımúyeshliklerden parqı júdá kem boladı. Usınday |
k materiallıq |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
tuwrımúyeshliklerdiń massası |
f ( k ) xk , k 1, n |
|
|
ǵa |
teń hám |
OY |
kósheri |
||||||||||||||||||||||||||||||
dógeregindegi aylanba qozǵalısındaǵı bul tuwrımúyeshliklerdiń noqatlarınıń sızıqlı
|
shama menen vk k , |
|
|
|
|
|
|
|
|
|
|
||||||||||
tezligi |
k 1, n |
ǵa |
teń. |
Onda |
|
G |
|
materiallıq |
|||||||||||||
|
|
|
|
|
|
|
n m v2 |
|
2 |
n |
f ( |
) |
2 |
|
|||||||
trapeciyasınıń kinetikalıq energiyasın |
E |
|
|
|
k k |
|
|
|
|
x |
túrinde |
||||||||||
|
|
|
|
|
|
|
|
k |
k |
k |
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
k 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
||||
jazıw múmkin. Bul teńlikte (T ) 0 |
da shekke ótsek, joqarıda |
f (x) |
funkciyası |
||||||||||||||||||
[a,b] |
segmentinde úzliksiz bolǵanı |
ushın |
x2 f (x) |
|
funkciyasıda |
[a,b] |
|||||||||||||||
segmentinde úzliksiz hám |
E lim 2 |
n |
f ( ) 2 x |
|
|
2 |
b x2 f (x)dx |
teńligi |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n 2 |
k 1 |
|
|
k |
k |
k |
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|

b
orınlı boladı. |
Endi |
IOY |
2 |
|
|
belgilewin kiritip, kinetikalıq energiyanı |
|||
x |
f (x)dx |
||||||||
|
|
|
|
|
|
||||
|
|
|
|
a |
|
|
|
|
|
ıqsham E |
2 |
IOY |
túrinde jazamız. Bunda IOY materiallıq trapeciyanıń OY |
||||||
2 |
|||||||||
kósherine baylanısli inerciyalıq momenti dep ataladı, al materiallıq trapeciyanıń |
|||||||||
tıǵızlıǵı, yaǵnıy birlik maydanǵa tuwrı keletuǵın massa bolıp, |
|||||||||
|
|
|
|
|
|
m |
|
m |
|
|
|
|
|
|
b |
||||
|
|
|
|
|
|
S (G) |
|
|
|
f (x)dx
a
formulası menen anıqlanǵan. Demek, iymek sızıqlı materiallıq trapeciyanıń OY kósherine baylanıslı inerciyalıq momenti ushın
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
x2 f (x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
I |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
OY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
formulasına iye bolamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Materiallıq |
|
trapeciyanıń statikalıq momenlerin esaplawdı |
1 bolǵan jaǵday |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ushın |
|
qarastıramız. Bunday jaǵdayda |
Gk , k 1,n |
|
|
materiallıq trapeciyalardıń |
||||||||||||||||||||||||
S (G |
) |
maydanları hám sáykes |
m |
|
massaları |
ushın |
|
S(G ) m |
k |
f ( |
k |
) x |
||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
k |
||
teńligi |
orınlı |
|
boladı |
hám |
olardıń massalar |
orayınıń |
koordinatalarý |
retinde |
||||||||||||||||||||||
x |
|
, y |
1 f ( ) , |
|
k 1, n |
noqatların aladı. |
Sonda |
G , |
|
materiallıq |
||||||||||||||||||||
C |
|
k |
C |
|
2 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
trapeciyalarınıń OX |
hám |
OY |
kósherlerine |
baylanıslı |
statikalıq momentlerı |
|||||||||||||||||||||||||
sáykes |
|
|
|
|
|
|
|
|
( f ( )2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
M |
|
|
|
k |
|
xk , M |
f ( ) x |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
OX |
|
|
|
2 |
|
|
|
|
OY |
|
|
k |
|
k |
|
k |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
túrinde jazıladı. Onda |
G materiallıq trapeciyasınıń statikalıq momentleri ushın |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
M |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
f ( ) x , |
M |
|
f ( ) x |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
OX |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 k 1 |
|
k |
|
k |
OY |
|
|
|
k |
|
k |
k |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
||||
ańlatpalarına |
iye |
bolamız. |
f (x) |
|
funkciyası |
[a,b] segmentinde |
úzliksiz |
hám |
||||||||||||||||||||||
keyingi |
teńliklerdiń |
oń |
|
tárepi |
f 2 (x) |
hám |
|
xf (x) |
funkciyalarınıń [a,b] |
|||||||||||||||||||||
segmentin T |
|
maydalaw usılındaǵı integrallıq qosındıları bolıwın kórip, |
(T ) 0 |
|||||||||||||||||||||||||||
shekke |
ótsek, |
|
G |
materiallıq trapeciyasınıń koordinata |
kósherlerine baylanıslı |
|||||||||||||||||||||||||
statikalıq momentleri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

|
|
|
|
|
|
|
|
|
1 |
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|||
|
|
|
|
|
MOX |
|
f |
2 (x)dx, |
MOY xf (x)dx |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||
formulaları járdeminde anıqlanadı degen |
juwmaqqa |
kelemiz. |
G |
materiallıq |
|||||||||||||||||||||||
trapeciyasınıń |
C(xC , yC ) |
|
awırlıq orayınıń koordinataları |
m S (G) |
bolǵanı ushın |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
||
|
|
|
|
xC |
|
MOY |
|
|
xf (x)dx |
yC |
|
MOX |
|
1 f 2 (x)dx |
|
|
|||||||||||
|
|
|
|
|
a |
, |
b |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
m |
|
f (x)dx |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
f (x)dx |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
formulalarına sáykes tabıladı. Bul formulalardan ekinshisin 2 ge kóbeytip, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 yC f (x)dx f 2 (x)dx |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
||
teńligine |
iye |
|
bolamız. |
Bunda |
f (x)dx S (G) |
iymek |
sızıqlı |
trapeciyanıń |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||
maydanı, |
b |
|
|
|
|
|
|
|
|
|
|
bolǵanı |
ushın, |
V (G) 2 yC S(G) |
teńligine iye |
||||||||||||
|
f |
2 |
(x)dx V (G) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bolamız, |
yaǵnıy G |
|
iymek sızıqlı trapeciyasınıń |
OX |
kósheri |
dógereginde |
|||||||||||||||||||||
aylanıwınan payda bolǵan deneniń kólemi onıń maydanı menen bul aylanıwda massalar orayı sızǵan sheńberdiń uzınlıǵınıń kóbeymesine teń boladı. Usı nátiyje Guldenniń ekinshi teoreması dep ataladı.
1-mısal. Massası m ǵa teń bolǵan G {(x, y): |
0 x a, 0 y 1 x2} iymek |
sızıqlı trapeciyası formasındaǵı plastinkanıń OY |
kósherlerine baylanıslı inerciya |
momentin, koordinata kósherlerine baylanıslı statikalıq momentlerin hám massalar orayınıń koordinataların tabıń.
Sheshiliwi. OY kósherlerine baylanıslı inerciya momenti:
|
|
|
a |
|
|
|
x 3 |
|
|
x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x2 (1 x2 )dx |
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
IOY |
|
|
|
|
|
|
m 3 |
| 0 |
5 |
| 0 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||
m |
0 |
|
|
|
|
|
|
|
ma (5 3a ) |
, |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5(3 a2 ) |
|
|
|
|
|
|
|
||||||
|
|
b |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
(1 x2 )dx |
|
|
x |a0 |
x |
|0a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
koordinata kósherlerine baylanıslı statikalıq momentleri: |
|
|
|
|
|
|
||||||||||||||||||||||||||
MOX |
1 |
|
f 2 (x)dx 1 a (1 x ) |
dx |
a(15 10a2 |
|
3a4 ) |
, |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
0 |
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
||||
|
|
a |
a |
x(1 x |
2 |
)dx |
|
x 2 |
|
|
|
|
x4 |
|
|
a |
2 |
(2 a |
2 |
) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
a |
|
a |
|
|
|
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
MOY |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
xf (x)dx |
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
massalar orayınıń koordinataları;

|
MOY |
3a(2 a2 ) |
|
MOX |
(15 10a2 3a4) |
|
|
||||||||
xC |
|
|
|
, |
yC |
|
|
|
|
|
|
|
|
|
|
m |
4(3 a2) |
|
m |
|
10(3 a2) |
|
|
|
|
||||||
2-mısal. |
(x d )2 y2 |
r 2, 0 r d |
sheńberi OY |
kósheri |
dógereginde |
||||||||||
aylanǵanda kelip shıqqan betliktiń maydanın tabıń. |
|
|
|
|
|
||||||||||
Sheshiliwi. Bunday betliklerdi matematikada tor |
dep ataydı. |
Berilgen |
|||||||||||||
sheńberdiń |
massalar orayı |
(d ,0) |
noqatı |
boladı. |
Usı |
|
noqat |
OY |
kósheri |
||||||
dógereginde aylanǵanda kelip shıǵatuǵın sheńber uzınlıǵı |
S (L) 2 d |
ǵa teń, al |
|||||||||||||
berilgen sheńberdiń uzınlıǵı |
2 r . Guldenniń birinshi teoreması tiykarında tordıń |
||||||||||||||
betiniń |
maydanı P(L) 2 y S(L) 2 d 2 r 4 2dr |
boladı. |
|
|
|||||||||||
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
Shınıǵıwlar
Berilgen sızıqlar menen shegaralanǵan figuralardıń maydanın esaplań:
1. x 2y 4 0, x y 5 0, y 0. (J.13,5) ; |
2. y 6x, x 4, |
y 0. (J. 48) |
3. y x2 3y, y 2 x2. (J. 2 2); 4. y x2, x y2. (J. 1) |
5. |
|
3 |
3 |
|
y x2 8x 18, y 2x 18. (J. 36); 6. y x2 10x 16, y x 2. (J. 4,5). 7. y x, y x12 , y 0, x 3, (J. 76).
8. Polyar kósheri hám a , a 0 Arhimed spiralınıń birinshi oramı menen
shegaralanǵan figuranıń maydanın tabıń. |
(J. 4 |
3a2 ) . |
|
|
||||
|
3 |
|
|
a2 |
||||
|
a cos3 |
|
|
|
||||
|
|
|
|
|
|
|||
9. |
|
úsh japıraqlı pozanıń maydanın tabıń. |
(J. |
|
). |
|||
|
4 |
|||||||
|
|
|
|
|
|
|
|
|
10. x a cos3 t, y asin3 t, 0 t 2 astroydası menen shegaralanǵan figuranıń maydanın tabıń.
3
|
Doǵa uzılıǵın esapań. 1. y x |
|
yarım kubikalıq parabolasınıń 0 x 5 |
|||||||||
|
2 |
|||||||||||
segmentine sáykes keliwshi doǵasınıń uzınlıǵın tabıń. |
(J. |
335 |
). |
|
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
27 |
|
|
|
2. |
a , a 0 |
Arhimed spiralınıń |
birinshi |
oramınıń |
uzınliǵın tabıń. |
|||||||
(J. a( 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 2 |
1)). |
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3. |
x et cost, y et sin t, 0 t ln |
parametrli |
teńlemesi |
menen berilgen |
||||||||
iymek sızıǵınıń uzınlıǵın tabıń. (J . 2( 1)). |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
y ln cos x 3 |
funkciyası frafiginiń |
0 x |
|
segmentine sáykes keliwshi |
|||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
doǵası uzınlıǵın tabıń. (J. ln( 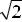 1)).
1)).
