
Aniq integrallar
.pdf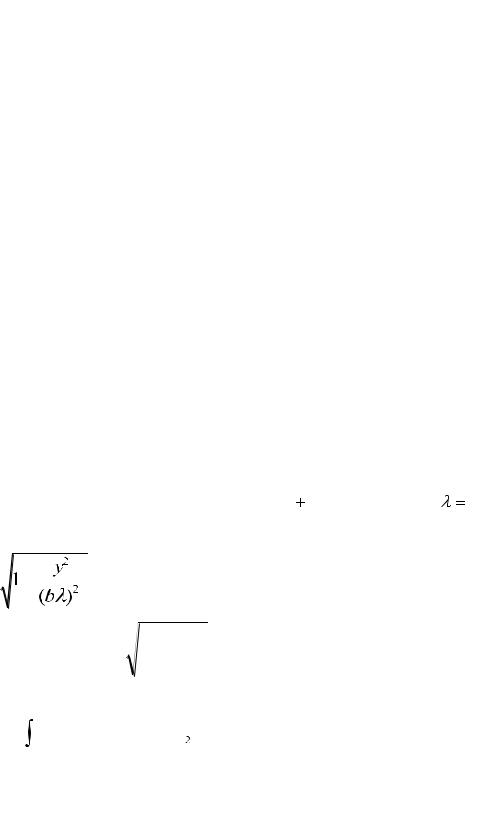
túrinde |
|
ańlatıw |
|
|
|
|
|
|
|
n |
|
2 |
|
|||
|
mumkin. Onda 0 V (Q ) V (q ) S s |
(M |
m ) x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
T |
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
teńligi |
orınlı |
hám |
|
M sup f (x) |
belgilewin |
kiritsek, |
(T ) |
bolǵanda |
||||||||
|
|
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(M |
m ) x2 |
|
2 M (b a) |
teńsizligi |
orınlı |
|
boladı. |
Endi |
nı |
||||||
|
|
|
|
k |
k |
|
k |
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T ) bolǵanda |
|
|
|
|
|
|||
4 M (b a) |
|
|
|
|
|
|||||||||||
|
|
túrinde tańlasaq, |
0 V (Q ) V (q ) |
|
||||||||||||
teńsizligine iye bolamız. Bul G iymek sızıqlı trapeciyası OY kóseri dógeregihde aylanǵanda payda bolatuǵın denesi kublanıwshı bolıwı ushın sárúr hám jeterli.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
||||
|
|
|
|
|
hám V (Q ) |
|
|
|
|
|
|
|
|
|
|
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
2 xf (x)dx |
||||||||||||||||
Onda V (q ) |
|
|
|
|
qosındılarınıń |
|
|
daǵı shekleri |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
integralına |
teń |
bolǵanı |
|
|
|
ushın |
|
denesiniń kólemin |
|
V ( ) 2 xf (x)dx |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
formulası járdeminde esaplaw múmkin boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y2 |
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1-mısal. |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 ellipsoydınıń kólemin tabıń. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
a2 |
|
|
b2 |
|
c2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Sheshiliwi. |
Ellipsoydtı |
OYZ |
|
|
tegisligine |
parallel bolǵan |
|
x x0 |
tegisligi |
||||||||||||||||||||||||||||||||||
menen |
kesemiz. Sonda |
|
kesimde |
|
|
|
y2 |
z2 |
1, |
x x0 |
, |
|
|
|
|
x2 |
ellipsı |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
1 2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c ) |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b )2 |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||||||
boladı. |
|
|
|
|
|
Bul |
ellipstiń |
maydanın |
|
tabıw |
|
ushın |
onıń |
|
I-aktanttaǵı |
||||||||||||||||||||||||||||
z c |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
, |
x x0 bóleginiń maydanın 4 ke kóbeytiw jeterli. Sonda, |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
y b sin t, y 0 t 0 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
S (x0 ) 4c 1 |
|
|
dy |
dy b costdt, y b |
t |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b ) |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S (x0 ) cb (1 x0 ) . |
|
|
|
|
|
||||||||||||||||||
4cb 2 cos2 tdt cb |
(1 x0 ) , yaǵnıy |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
x2 |
4 |
|
|
|
|
|
|||||
Onda |
ellipsoydtıń |
kólemi |
V 2 S (x)dx 2 bc (1 |
|
|
)dx |
|
abc. |
Bunnan, |
||||||||||||||||||||||||||||||||||
a |
2 |
||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a b c r dara jaǵdayında shardıń V |
4 |
r3 kólemi kelip shıǵadı. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2-mısal. |
|
x a(t sin t), y a(1 cost) |
parametrli |
teńlemesi |
menen |
||||||||||||||||||||||||||||||||||||||
berilgen iymek sızıǵı cikloyda dep ataladı. Cikloydanıń bir arkası |
OX |
kósheri |
|||||||||||||||||||||||||||||||||||||||||
dógereginde aylanıwında payda bolǵan deneniń kólemin tabıń. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
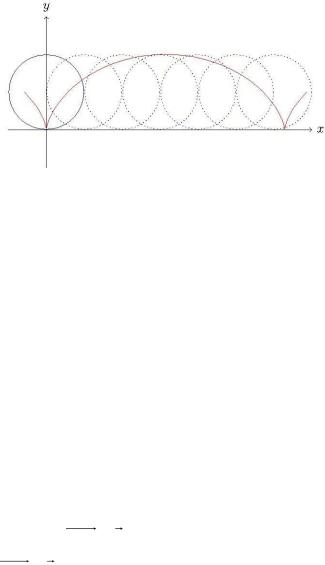
Sheshiliwi. Cikloydanıń bir arkasına t parametriniń [0,2 ] segmentindegi mánisleri sáykes keledi. Onda dx a(1 cost)dt bolǵanı ushın,
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
10- súwret |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
a |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
||
V y2dx a2 |
|
(1 cost)3dt a2 (1 3cost 3cos2 t cos3 t)dt |
||||||||||||||||
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
1 cos 2t |
|
|
|
|
|
||||
a |
2 |
(1 |
3cost 3 |
(1 sin2 t) cost)dt |
||||||||||||||
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
0 |
|
3 |
|
|
|
3 |
|
|
|
sin3 t 2 |
|
|||
a3 (t 3sin t |
|
|
|
|
|
|
2 3 |
|||||||||||
|
|
t |
|
|
sin 2t sin t |
|
) |0 |
5 a . |
||||||||||
2 |
4 |
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. Anıq integral járdeminde iymekliktiń uzınlıǵın esaplaw. Meyli úsh ólshewli
keńislikte OXYZ |
tuwrımúyeshli dekart koordinatalar sisteması tańlanǵan |
hám |
|||||||||||||||||||
[ , ] |
segmentinde |
x x(t), y y(t), z z(t) |
úzliksiz |
funkciyaları anıqlanǵan |
|||||||||||||||||
bolsın. Bunday jaǵdayda |
[ , ] |
segmentiniń |
úsh |
ólshewli keńislikke |
úzliksiz |
||||||||||||||||
sáwlelendiriliwi |
|
berilgen |
delinedi. |
t [ , ] |
mánisine |
sáykes |
keliwshi |
||||||||||||||
x(t), y(t), z(t) sanlar |
úshligin |
keńisliktegi M (t) noqatınıń koordinatası |
retinde |
||||||||||||||||||
yamasa |
OM r(t) |
vektorınıń |
koordinatası |
retinde |
qarastırıw |
múmkin, |
yaǵnıy |
||||||||||||||
OM r(t) (x(t), y(t), z(t)) |
. Eger t |
waqıt retinde qabıl etilse, onda |
|
|
|
||||||||||||||||
|
|
|
x x(t), |
y y(t), z z(t) , |
t [ , ] |
|
|
|
|
|
|
(1) |
|||||||||
teńlemeleri |
M (t) |
noqatınıń qozǵalıs |
nızamın |
anıqlaydı. Bul |
jaǵdayda |
t |
nıń |
||||||||||||||
[ , ] |
segmentindegi múmkin bolǵan mánislerine saykes keliwshi keńisliktegi |
||||||||||||||||||||
noqatlar kópligin (1) nızamına sáykes qozǵalıwshı |
M (t) noqatınıń |
izi |
retinde |
||||||||||||||||||
qarastırıwǵa |
|
boladı. |
Meyli |
E |
usınday |
noqatlar |
kópligi |
bolsın. |
|
Eger |
|||||||||||
t ,t |
2 |
[ , ], t |
1 |
t |
mánislerine |
keńisliktiń |
hárqıylı |
M (t1), M (t2 ) |
noqatları |
||||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
sáykes kelse hám t1 t2 teńsizligi orınlı bolsa, onda “ M (t2 ) E |
noqatı |
||||||||||||||||||||
M (t1) E |
noqatınan keyin” yamasa “ M (t1) E |
noqatı M (t2 ) E |
noqatınan |
||||||||||||||||||
aldın” dep aytamız. Usınday ornatılǵan noqatlardıń jaylasıwı |
E kópliginde de |
||||||||||||||||||||
tártip ornatadı. Bunday tártiplesken |
E kópligine |
ápiwayı iymek dep |
ataladı. |
||||||||||||||||||
ápiwayı iymekti L háribi menen belgileymiz hám onıń teńlemesin |
|
|
|
||||||||||||||||||

L {x x(t), y y(t), z z(t), t [ , ]} |
|
(2) |
|||||
koordinatalıq túrinde yamasa |
|
|
|
|
|
|
|
L {r r(t), t [ , ]} |
|
|
|
(3) |
|||
vektorlıq túrinde jazadı. Bunda |
r (x, y, z), |
r(t) (x(t), y(t), z(t)) . |
(2) |
hám (3) |
|||
teńlemelerde t nı L iymeginiń parameteri dep ataydı. Parametrdiń |
t hám |
||||||
t mánislerine sáykes keliwshi keńisliktiń |
M ( ) hám M ( ) noqatları sáykes |
||||||
L iymeginiń bası hám sońı dep ataladı. |
|
|
|
|
|
||
Dara jaǵdayda, eger |
L iymegi OXY |
tegisligine tiyisli iymek bolsa, onda |
|||||
onıń teńlemesi L {x x(t), y y(t), t } |
koordinatalıq kórinisinde yamasa |
||||||
L {r r(t), t [ , ]} |
|
vektorlıq |
túrinde |
jazadı. |
|
Bunda |
|
r (x, y), r(t) (x(t), y(t)) . |
[ , ] segmentinde |
úzliksiz bolǵan |
y f (x) |
||||
funkciyasınıń grafigin |
OXY |
tegisligindegi |
L {x t, y f (t), |
t } |
|||
iymegi retinde qarastırıw múmkin.
Ápiwayı iymektiń anıqlamasına sáykes (1) sáwlelendiriwi biektiv sáwlelendiriw
boladı, yaǵnıy |
t |
parametriniń hárbir t [ , ] mánisine birden-bir |
M (t) L |
|||||||
noqatı sáykes keledi hám kerisinshe hárbir M L noqatına birden-bir |
t [ , ] |
|||||||||
mánisi sáykes qoyılǵan.Eger t |
parametriniń t1,t2 [ , ] mánisleri bar bolıp, |
|||||||||
M (t1) M (t2 ) |
teńligi orınlı bolsa, onda (1)-sáwlelendiriw óz-ara bir mánisli |
|||||||||
bolmaydı. Bunday jaǵdayda L iymegin parametrlew ushın [ , ] |
segmentin |
|||||||||
|
|
|
|
|
|
|
||||
T {tk , k 0, n} |
usılında |
k [tk 1,tk ], k 1, n} dara kesindilerine sonday |
||||||||
maydalaymiz, |
|
natiyjede |
harbir |
x x(t), y y(t), z z(t) , |
t [tk 1,tk ] , |
|||||
k 1, n úzliksiz sáwlelendiriwi biektiv sáwlelendiriw bolıp olardıń harbiri sáykes
|
|
|
|
|
|
|
Lk {x x(t), |
y y(t), z z(t), tk 1 t tk } , k 1, n |
|
|
|
||
ápiwayı iymegin anıqlasın. |
Sonda L iymegi Lk 1 iymeginiń sońı Lk , |
k 1,n , |
||||
iymeginiń basi bolatuǵın, ápiwayı iymekliklerge bólingen boladı hám harbir Lk bólegi L iymeginiń ápiwayı doǵası dep ataladı. Usı jaǵdayda da L iymegi (2) teńlemesi járdeminde parametrlengen dep aytadı. Bir L iymegi bir neshe usılda parametrleniwi múmkin. Ádette L iymeginiń berilgen (2) parametrleniwindegi t parametrin ekinshi bir parametriniń úzliksiz hám qatań ósiwshi funkciyası túrinde ańlatıwdan kelip shıǵatugın parametrlewleri qarastırıladı. Demek, eger L iymegi
(3) túrindegi t parametrine baylanıslı teńlemesi menen birge ekinshi bir s

parametrine baylanıslı |
L {r1 |
r1(s), 1 s 1} túrinde de berilgen bolsa, onda |
||||||
s s(t) |
funkciyası |
[ , ] |
segmentinde |
uzliksiz, qatań ósiwshi hám |
||||
s( ) 1, s( ) 1, r1(s(t)) r(t), t [ , ] |
shártlerine boysınıwı tiyis. Sonda |
|||||||
[ |
, ] |
segmentinde |
s s(t) |
funkciyasına |
keri bolǵan t t(s) |
funkciyası |
||
1 |
|
1 |
|
|
|
|
|
|
hám s [ 1, 1] ushın r1(s) r(s(t)) teńligi orınlanadı. |
|
|||||||
Eger |
(3) |
teńlemesindegi t |
parametri ornına |
L iymeginiń óziniń |
s s(t) |
|||
doǵasınıń uzınliǵı alınsa, onda onıń teńlemesi L {r r(s), 0 s l(L)} |
túrinde |
||||||||||||
jazıladı hám L iymeginiń tabiyi |
teńlemesi dep, |
al |
s |
parametri bolsa tabiyi |
|||||||||
parametr dep ataladı. |
|
|
|
|
|
|
|
|
|||||
|
|
|
Meyli L |
iymegi (3) |
teńlemesi menen berilgen |
hám t |
parametriniń |
||||||
t |
,t |
2 |
[ , ], t |
1 |
t |
mánislerinde |
r(t1) r(t2 ) |
teńligi |
orınli |
bolsın. |
Onda |
||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
||
x x(t1) x(t2 ), y y(t1) y(t2 ), |
z z(t1) z(t2 ) |
teńlikleri |
orınlı |
bolǵanı |
|||||||||
ushın M1 (x1, y1, z1) |
noqatı |
L iymeginiń óz-ózi menen kesilisiw noqatı boladı. |
|||||||||||
Eger r(t1) r(t2 ) teńligi t1 , t2 |
bolǵanda orınlansa, onda |
L iymegi tuyıq |
|||||||||||
iymek dep, al óz-ózi menen kesilisiw noqatına iye bolmaǵan tuyıq iymegi ápiwayı kontur dep ataladı.
Eger (3) teńlemesindegi funkciyası segmentinde differenciallanıwshı funkciya bolsa, onda L iymegine differenciallanıwshı iymek
dep ataydı. Eger |
r (t0 ) 0 |
bolsa, |
onda |
M 0 L noqatı L iymeginiń ayrıqsha |
||
bolmaǵan noqatı |
dep, al r (t0 ) 0 |
bolsa, |
onda |
M0 L noqatı L iymeginiń |
||
ayrıqsha noqatı dep ataladı. |
|
tuwındısı |
[ , ] |
segmentinde úzliksiz bolsa, |
||
r (t) |
||||||
onda (3) teńlemesi menen |
berilgen L |
iymegine |
úzliksiz differenciallanıwshı |
|||
iymek delinedi. Ayrıqsha noqatına iye emes úzliksiz differenciyallanıwsı iymegi sıypaq iymek dep ataladı. Eger iymek sızıq shekli sandaǵı sıypaq iymeklerden quralǵan bolsa, onda oǵan bolek sıypaq iymek sızıq delinedı. Endi (3)
teńlemesindegi funkciyası segmentinde differenciallanıwshı funkciya bolsın. [ , ] segmentin bazıbir T {tk , k 0, n} usılında maydalasaq, onda tk maydalaw noqatlarına L iymeginiń Mk M (tk ) noqatları sáykes keledi. Bunda
|
|
|
|
||
OMk r(tk ), k |
0, n |
. |
Onda |
M0 , M1, , M |
noqatların |
|
|
|
|
n |
|
M0M1, M1M 2 , , Mn 1Mn , |
kesındıleri menen tutastırıp |
L iymegine ishki |
|||
sızılǵan sınıq sızıq dep atalatuǵın hám Pn |
arqalı belgilenetuǵın sınıq sızıqqa iye |
||||

bolamız. Pn sınıq sızıǵınıń k bólegi bolǵan Mk 1Mk |
kesindisiniń uzınliǵı |
|||||||||||
|
r(t ) r(t |
|
) |
|
ge teń bolıwın kóriw qıyın emes. Onda P |
sınıq sızıǵınıń uzınlıǵı |
||||||
|
|
|
||||||||||
|
|
|
k |
|
|
k 1 |
|
|
|
n |
|
|
|
|
|
n |
|
|
|
qosındısına teń boladı hám onıń mánisi [ , ] segmentin |
|||||
|
n |
|
r(t |
|
) r(t |
) |
||||||
|
|
|
|
k |
|
|
|
k 1 |
|
|
||
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
maydalaw usılınan ǵárezli boladı, yaǵnıy hárqıylı maydalaw usılına hárqıylı n
qosındısı sáykes keledi. Eger Pn sınıq sızıǵınıń uzınlıqları kópligi anıq joqarǵı shegarasına iye bolsa, onda usı anıq joqarǵı shegara L iymeginiń uzınliǵı dep qabıl etiledi. Uzınlıǵı bar bolǵan iymek sızıq tuwrılanıwshı iymek dep ataladı.
Teorema. Eger (3) teńlemesi menen berilgen L iymegi uzliksiz differensiallanıwshi bolsa, onda ol tuwrılanıwshı iymek boladı hám onıń
uzınlıǵı l(L) ( ) sup |
|
|
|
|
|
|
|
teńsizligin qanaatlandıradı. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Dálilleniwi. [ , ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
segmentin bazıbir T {tk , k |
0, n |
} usılında maydalasaq |
||||||||||||||||||||||||||||||||||||||||||||||||||
hárbir k [tk 1,tk ], |
|
k 0, n dara |
|
kesindisinde r(t) |
|
|
funkciyası |
úzliksız |
hám |
|||||||||||||||||||||||||||||||||||||||||||
(tk 1,tk ), |
k 0, n |
|
|
intervallarında |
|
differenciallanıwshı bolǵanı |
ushın |
|
Lagranj |
|||||||||||||||||||||||||||||||||||||||||||
teoremasına sáykes |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tk 1), k |
(tk ,tk 1) |
teńsizligi orınlı. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
r(t) funkciyası |
[ , ] |
|
segmentinde úzliksız bolǵanı |
ushın [ , ] |
segmentinde |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
shegaralanǵan, yaǵnıy |
K 0 : t [ , ] r |
(t) |
K . |
|
Veyershtrass |
|
teoremasına |
|||||||||||||||||||||||||||||||||||||||||||||
sáykes K sup |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
bolıwı múmkin. Onda L iymegine ishki sızılǵan Pn |
sınıq |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
t |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sızıǵınıń uzınlıǵı n |
|
|
|
|
|
|
|
|
|
|
|
|
|
ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
n |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
tk tk 1) K (tk tk 1) K ( ) |
|
|
|
||||||||||||||||||||||||||||||
|
r(tk ) r(tk 1) |
|
r ( k ) ( |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
bahası orınlı. Bunnan |
|
l(L) sup n |
( ) sup |
|
|
|
|
|
|
|
. Teorema dálillendi. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L {r r(t), t } |
||||||||||||||
Teorema(Ózgeriwshi doǵa tuwındısı). |
|
Eger |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
iymegi úzliksiz |
differenciallanıwshı |
|
hám s(t) onıń |
|
ózgeriwshi |
duga |
uzınlıǵı |
|||||||||||||||||||||||||||||||||||||||||||||
bolsa, onda |
s (t) |
|
r (t) |
|
|
|
|
teńligi t [ , ] |
ushın orınlı boladı. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Dálilleniwi. |
t [ , ] |
|
|
|
|
noqatın alıp |
|
t |
ósimin |
sonday beremiz |
nátiyjede |
|||||||||||||||||||||||||||||||||||||||||
t t [ , ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
bolsın. t hám |
t |
|
noqatlarına |
L |
|
iymeginiń M |
hám |
M |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
noqatları sáykes keledi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hám |
|
|
|
|
|
arqalı sáykes |
|
|
|
|
duga |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
d ( M |
M ) |
|
|
|
|
|
|
M M |
|
|
|
M M |
|
||||||||||||||||||||||||||||||||||||||

hám |
|
|
|
|
|
|
|
xorda uzınlıqları belgilense, onda |
s , r ósimleri |
d( M |
|
M |
|
|
) s |
|
, |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
M M |
|
r |
|
|
|
|
bolǵanı |
ushın |
|
|
|
|
r |
|
|
|
s |
|
|
teńsizligi |
orınlı |
|
boladı. Onda |
aldın |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
dálillengen teoremadan |
|
s |
|
|
sup r |
|
(t) |
|
|
|
|
|
|
|
teńsizligi orınlanadı. Bunda E shetki |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
noqatları t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
s sup |
|
|
|
|
t |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
hám t t |
bolǵan kesindi. Bul teńsizliklerden |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t E |
|
|
|
|
|
|
|
|
|
||
qos teńsizligi, al bunnan |
|
s(t) |
|
ósiwshi bolǵanı ushın |
|
|
r |
|
|
s sup |
|
|
|
boladı. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
t |
|
t E |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
r(t) funkciyası |
[ , ] |
segmentinde úzliksiz bolǵanı ushın |
|
|
|
|
|
|
funkciyası da |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
r (t) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
bul |
|
segmentte |
|
úzliksiz. |
|
|
|
|
|
|
|
|
|
|
Onda |
|
|
|
|
|
|
Veyershtrass |
|
|
|
teoremasınan |
|
|
|
E : |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hám |
|
|
|
|
|
|
|
|
|
|
|
|
funkciyası |
|
|
t |
|
noqatında |
úzliksiz |
|
bolǵanı |
ushın |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
s sup |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 shekke ótip |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. Endi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizliginde |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
t |
|
t E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
s (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
teńligine iye bolamız. Teorema dálillendi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Dálillengen teoremaǵa sáykes úzliksiz differenciallanıwshı L |
|
|
|
iymegi |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tuwrılanıwshı |
hám |
onıń |
|
|
s s(t) |
|
uzınlıǵı |
|
ózgeriwshi |
|
doǵasınıń |
|
|
tuwındısı |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
boladı. |
Bunnan |
|
|
|
|
L |
|
iymeginiń |
|
l(L) |
|
uzınliǵın Nyuton-Leybnic |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
s (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
formulası járdeminde, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
l(L) |
|
|
(t)dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s( ) s( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
s (t)dt s(t) | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
tabıw formulasına iye bolamız. Bunda s( ) 0 |
hám s( ) l(L) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Eger |
|
L |
|
iymegi |
|
|
[ , ] |
|
|
|
|
|
|
|
segmentinde |
|
|
úzliksiz |
|
|
|
|
differenciallanıwshı |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x(t), y(t), z(t) |
fukciyaları járdeminde L {x x(t), y y(t), z z(t), t [ , ]} |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
parametrli teńlemesı menen berilgen bolsa, onda |
|
r(t) (x(t), y(t), z(t)) |
|
|
bolǵanı |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ushın (1) formula |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
l(L) |
|
|
|
(t)) |
2 |
|
|
|
|
|
|
(t)) |
2 |
|
|
|
|
|
(t)) |
2 |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(x |
|
|
|
( y |
|
|
|
(z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
túrinde jazıladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Eger |
L |
iymegi |
tegisliktegi |
iymek |
|
|
bolıp |
|
[ , ] |
|
segmentinde |
|
|
úzliksiz |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
differenciallanıwshı |
x(t), |
|
y(t) |
|
|
|
|
funkciyaları |
|
járdeminde |
|
x x(t), |
|
y y(t), |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
t [ , ] |
|
parametrli teńlemesı menen berilgen bolsa, onda (2) formulasın |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l(L) |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x (t)) |
|
|
|
( y (t)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
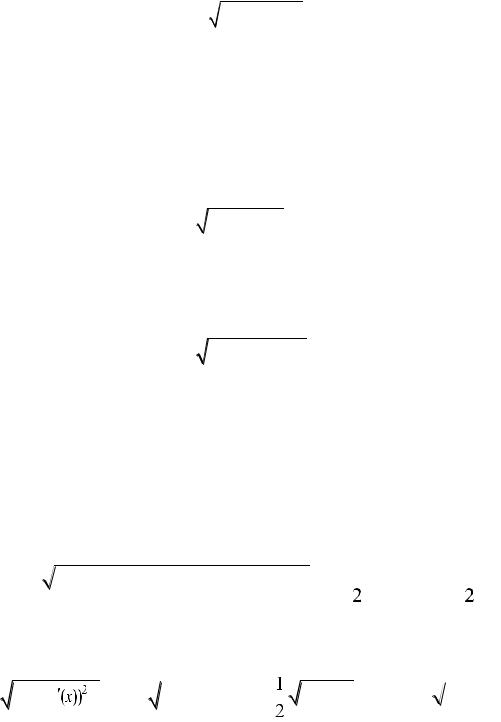
túrinde jazamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Eger |
|
L |
|
|
tegisliktegi |
iymek |
sızıq |
|
bolıp |
|
|
|
|
[a,b] |
|
segmentinde |
úzliksiz |
|||||||||||||||||||||||||||||||
differenciallanıwshı y f (x) |
funkciyasınıń grafigi retinde berilgen bolsa, onda |
|||||||||||||||||||||||||||||||||||||||||||||||
onıń uzınlıǵın |
tabıw ushın |
x t, |
|
|
y f (t), |
a t b |
parametrlewin júzege |
|||||||||||||||||||||||||||||||||||||||||
asırıp, dt dx, |
f (x) f (t) bolǵanı ushın (3)-formuladan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
l(L) |
|
(x)) |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
formulasına iye bolamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Eger |
|
L |
|
tegisliktegi |
iymek |
|
sızıq |
|
|
bolıp, |
|
polyar |
koordinatalar |
sistemasında |
||||||||||||||||||||||||||||||||||
( ) teńlemesi menen berilgen hám |
|
( ) |
|
funkciyası [ , ] |
segmentinde |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
( ) |
tuwındısına iye bolsa, onda |
|
L iymeginiń |
|
l(L) uzınlıǵın tabıw |
||||||||||||||||||||||||||||||||||||||||
úzliksiz |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
ushın di parametr dep esaplap, |
x ( )cos , |
y ( )sin |
|
|
túrindegi |
|||||||||||||||||||||||||||||||||||||||||||
parametrlewde (3) formuladan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l(L) |
|
|
2 |
( )2 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bolıwın |
kóremiz. Eger |
tegisliktegi iymek sızıq |
bolıp, |
|
polyar |
koordinatalar |
||||||||||||||||||||||||||||||||||||||||||
sistemasında |
|
teńlemesi ( ), a b túrinde bolsa, onda (3) formuladan |
||||||||||||||||||||||||||||||||||||||||||||||
paydalanıp |
|
L iymeginiń uzınliǵı |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l(L) 1 2 ( ( )2 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
formulası menen anıqlanıwı múmkinligin kóremiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1-mısal. |
|
|
x a cos3 t, y asin3 t |
|
|
|
astroidanıń |
birinshi |
|
sherekte |
jatıwshı |
|||||||||||||||||||||||||||||||||||||
doǵasınıń uzınlıǵın tabıń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Sheshiliwi. |
|
|
2 |
|
|
|
3asin |
2 |
t cost |
|
|
hám birinshi |
sherekte |
|||||||||||||||||||||||||||||||||||
x 3a cos |
t sin t, y |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 t |
|
|
|
bolǵanı ushın, qıyın emes. (3) formulaǵa sáykes, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a |
2 |
|
|
|
|
|
|
|
|
|
3a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
l(L) |
|
9a2 cos4 t sin2 t 9a2 sin4 xcos2 xdt |
|
|
|
sin 2tdt |
|
|
. |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2-mısal. y ax2, 0 x 1 |
parabola doǵasınıń uzınlıǵın tabıń. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Sheshiliwi. y 2ax |
bolǵanı ushın, (4) formuladan paydalansaq, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l(L) |
1 ( f |
dx |
1 (2ax)2 |
dx |
|
|
|
1 4a2 ln |
2a |
|
1 4a2 |
. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3-mısal. aeb |
logarifmlik spiralınıń |
( , ) |
hám |
( |
2 |
, |
2 |
) |
|
noqatları |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
arasındaǵı doǵasınıń uzınlıǵın tabıń.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Sheshiliwi. |
(5) |
|
|
|
|
|
|
|
formulaǵa |
sáykes, |
|
|
l(L) |
2 ( )2 d |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 b2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eb d |
eb |
| 12 |
|
1 b2 |
( ) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2 |
e |
2b |
|
|
|
|
2 2b |
d a |
1 b2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
b |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
a |
|
(ab) e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
1 |
|
|||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
boladı. |
|
|
|
|
|
|
sh x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4-mısal. |
dx,0 R |
|
túrinde |
berilgen iymektiń |
doǵasınıń |
uzınlıǵın |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
tabıń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Sheshiliwi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
l(L) |
1 ( ( )) |
|
d ch d shR. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Aylanba betliktiń maydanı. Meyli |
f (x) |
funkciyası |
[a,b] segmentinde |
|||||||||||||||||||||||||||||||||||||||||||||||||
teris |
|
|
|
emes |
|
|
|
anıqlanǵan |
|
|
úzliksiz |
funkciya |
bolsın. |
|
|
[a,b] |
segmentin |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
xk T |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
T {xk , k 0, n} usılında |
maydalap, |
maydalaw |
noqatlarına |
sáykes |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
keliwshi funkciya grafiginiń noqatların |
Mk (xk , |
f (xk )), k 0,n belgilep, tóbeleri |
||||||||||||||||||||||||||||||||||||||||||||||||||
usı |
Mk |
noqatları bolgan |
|
LT |
sınıq |
sızıǵın |
qarastıramız. Bul sınıq sızıǵınıń |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Mk 1Mk , |
|
|
|
|
k 1, n |
|
|
|
|
|
|
|
|
|
|
|
|
|
boleginiń |
|
uzınlıǵı |
|
sáykes |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
lk |
|
|
(x |
x |
|
|
|
)2 ( f (x ) f (x |
|
))2 , |
|
k 1, n |
bolıp, |
bul |
bólekler |
|
OX |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
kósheriniń dógereginde aylanıwında, jasawshıları |
Mk 1Mk , |
k 1, n |
|
kesindilerı |
||||||||||||||||||||||||||||||||||||||||||||||||
bolǵan jaǵdayda, kesik konustıń betın, eger |
f (xk 1) f (xk ) |
bolsa hám cilindrdiń |
||||||||||||||||||||||||||||||||||||||||||||||||||
betin, eger |
f (xk 1) f (xk ) |
|
bolsa, |
|
payda etedı. Bul kelip shıqqan betliklerdıń |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
( f (xk ) f (xk 1))lk , |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
maydanları |
sáykes |
|
pk |
k |
0,n |
|
formulası járdeminde |
|||||||||||||||||||||||||||||||||||||||||||||
tabıladı. Bunnan LT |
sınıq sızıǵı OX kósheriniń dógereginde aylanıwında payda |
|||||||||||||||||||||||||||||||||||||||||||||||||||
bolǵan betliktiń maydanı, |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(LT ) ( f (xk 1) f (xk ))lk . |
|
|
|
|
|
|
|
|
|
|
|
|
(A) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Eger |
|
|
|
lim |
P(LT ) P(L) |
shegi bar bolsa, onda |
|
P(L) |
sanı |
y f (x) , |
x [a,b] |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
funkciyası grafigi OX |
kósheri dógereginde aylanǵanda kelip shıǵatuǵın aylanba |
|||||||||||||||||||||||||||||||||||||||||||||||||||
bettiń maydanı dep ataladı. Bunda |
|
|
(T ) , T maydalawınıń diametri. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Teorema. |
|
|
|
Eger |
|
|
|
|
y f (x) |
|
|
|
funkciyası |
|
|
|
[a,b] |
segmentinde |
úzliksiz |
|||||||||||||||||||||||||||||||||
differenciyallanıwshı funkciya bolsa, onda |
|
lim P(LT ) P(L) |
|
shegi bar hám bul |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
funkciyanıń |
grafigi |
|
OX |
|
kósheriniń |
dógereginde |
aylanıwında |
|
payda |
bolǵan |
||||||||||||||||||||||||||||||||||||||||||
aylanba betliktiń maydanı |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
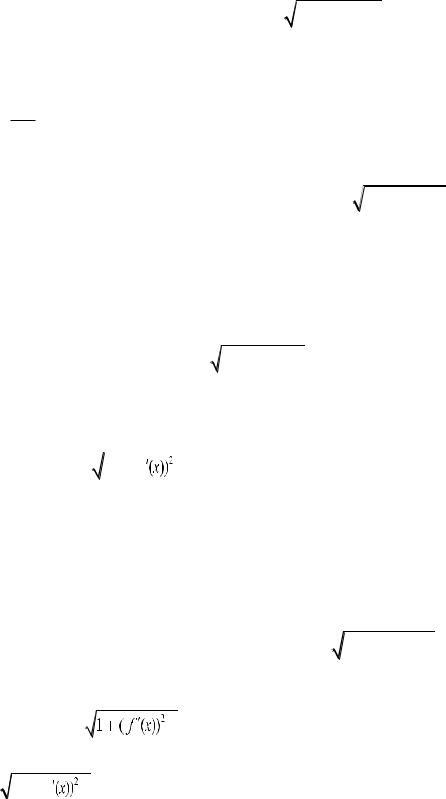
b |
|
|
2 |
(B) |
|
P 2 f (x) 1 ( f (x)) dx |
|
|
a |
|
|
formulası menen ańlatıladı.
Dálilleniwi. Teoremanıń shártleri orınli bolǵanda Lagranj teoremasına sáykes,
f (x |
) f (x |
k 1 |
) f ( |
) x |
teńligin jazamız. Bunda k k |
hám |
k |
[x |
, x ], |
k |
|
k |
k |
|
|
|
k 1 k |
k 0, n segmentleri [a,b] segmentin T maydalaw usılındaǵı dara segmentler, al
xk |
xk xk 1 |
|
|
dara |
|
|
segmentlerdiń |
sáykes |
|
uzınlıqları. |
Onda |
|||||||||||
P(L |
n |
( f (x |
) f (x |
|
|
n |
f (x |
k |
|
1 |
) f (x |
) |
1 |
|
)) |
2 |
x |
boladı. Bundaǵı |
||||
) |
))l 2 |
|
|
k |
|
( f ( |
|
|||||||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
k |
k |
|
|
|
|
|
2 |
|
|
k |
|
|
|
k |
|
||
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (xk 1) f (xk ) |
|
sanı |
f (x |
|
) |
hám |
f (x |
k |
) sanlarınıń orta arifmetigi bolǵanı ushın, |
|||||||||||||
|
2 |
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
úzliksiz funkciyalardıń orta mánisi haqqındaǵı Koshi teoremasına sáykes k k
|
|
|
|
|
|
|
|
|
|
|
|
f ( k ) |
|
f (xk 1) f (xk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
noqatları bar hám |
|
, k 0,n teńlikleri orınlı. Usı teńlikler |
|||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
P(L ) 2 n f ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
tiykarında |
|
|
1 ( f ( ))2 x |
|
|
qosındısına |
iye |
bolamız. |
Bul |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
usılındaǵı |
||||||
integrallıq |
|
qosındı |
emes. Biraq [a,b] segmentin |
|
T |
maydalaw |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k , k k |
|
|
|
|
||||||||||||||||||||||||||
tańlawın |
|
{ k , k 1, n |
} |
|
|
turinde alsaq, |
onda |
|
bolǵanı |
ushın, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T ( , f ) |
|
|
|
||||||||||||||||||||||||||||||
|
f1(x) 2 f (x) 1 ( f |
|
|
|
|
|
funkciyasınıń |
|
integrallıq qosındısı hám |
||||||||||||||||||||||||||||||||||||
|
P(LT ) |
qosındısı bir-birine jaqın boladı. Sebebi |
|
|
f (x) |
hám |
f |
|
|
|
funkciyaları |
||||||||||||||||||||||||||||||||||
|
|
|
(x) |
|
|
||||||||||||||||||||||||||||||||||||||||
[a,b] |
segmentinde úzliksiz bolǵanı ushın |
f (x) |
|
funkciyası da bul segmentte |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
úzliksiz hám |
LT sınıq sızıǵınıń eń úlken boleginiń uzınlıǵı nolge umtılsa onıń |
||||||||||||||||||||||||||||||||||||||||||||
menen birge (T ) |
da nolge umtıladı. Onda, |
(T ) 0 da shekke ótsek, anıq |
|||||||||||||||||||||||||||||||||||||||||||
integraldıń anıqlamasınan, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
1 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
( , f ) 2 |
f (x) |
1 ( f (x))2 dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
boladı. |
|
Endi |
|
|
(T ) 0 |
|
|
da |
T ( , f ) S(LT ) |
|
ayırmasıda |
nolge |
umtılıwın |
||||||||||||||||||||||||||||||||
kórsetemiz. |
|
|
|
|
|
|
|
|
|
|
funkciyası [a,b] |
segmentinde úzliksiz bolǵanı ushın |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
bul funkciya [a,b] |
segmentinde shegaralanǵán, yaǵnıy С 0: |
|
|
x [a,b] |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
C. |
f (x) |
funkciyası [a,b] |
|
|
|
|||||||||||||||||||||||||||||||||
1 ( f |
|
|
|
|
segmentinde úzliksiz bolǵanı ushın |
||||||||||||||||||||||||||||||||||||||||
bul funkciya Kantor teoremasına sáykes [a,b] |
|
segmentinde teń ólshewli úzliksiz, |
|||||||||||||||||||||||||||||||||||||||||||
yaǵnıy |
|
|
|
|
|
|
|
|
|
|
|
|
( ) 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
0 |
, |
|
|
|
|
|
|
x , x |
[a,b], |
|
|
|
|
x x |
|
|
|||||||||||||||||||||||||
|
|
|
) |
|
|
|
|
|
|
|
|
.Onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
f (x ) f (x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
1 |
|
|
|
|
2 C(b |
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
( , f ) P(L ) 2 ( f ( ) f ( )) 1 ( f ( ))2 x |
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
T |
|
|
|
|
T |
|
|
|
|
|
|
|
k |
k |
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 C |
|
|
|
|
|
, |
|||||||
|
|
|
|
|
f ( ) |
|
f ( |
|
) |
1 |
|
( f ( |
|
)) x |
|
|
|
|
2 C(b a) |
xk |
|||||||
|
|
|
|
k 1 |
|
k |
|
|
k |
|
|
|
|
|
k |
|
|
k |
k 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
bunnan |
0 |
sanı qálegen san bolǵanı ushın, lim ( |
|
( , f ) P(L )) 0 |
boladı. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
T |
|
|
|
T |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Demek, LT sınıq sızıǵı |
aylanıwınan |
payda bolǵan betliktiń maydanı bar hám |
|||||||||||||||||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim P(LT |
) 2 |
|
|
|
|
2 |
|
|
|
|
|
|
y f (x) |
|
|
|
|
|
|
|
|||||||
f (x) 1 ( f (x)) dx . |
|
Bul |
|
|
|
funkciyasınıń grafigi OX |
|||||||||||||||||||||
(t ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kósheriniń dógereginde aylanıwında payda bolǵan aylanba betliktiń maydanı bar hám ol (B) formulasına sáykes tabıladı. Teorema dálillendi.
Eger L iymegi [ , ] segmentinde úzliksiz differenciyallanıwshı |
u(t), v(t) |
||||||||||||||
funkciyaları járdeminde |
x u(t), y v(t), t [ , ] parametrli teńlemesi menen |
||||||||||||||
berilgen bolsa, onda L |
iymegi OX |
kósheriniń dógereginde aylanıwında payda |
|||||||||||||
bolǵan aylanba betliktiń maydanı, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(L) 2 v(t) |
|
(u (t))2 |
(v (t))2 dt |
(S) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
formulasına sáykes anıqlanadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Eger L iymegi polyarlıq koordinatalar sistemasında ( ), |
|
||||||||||||||
teńlemesi járdeminde berilgen bolsa, onda |
( ) |
funkciyası [ , ] segmentinde |
|||||||||||||
úzliksiz differenciyallanıwshı bolǵan |
jaǵdayda |
|
L iymeginiń polyarlıq kósher |
||||||||||||
dógereginde aylanıwinan payda bolǵan betliktiń maydanı, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
P(L) 2 sin |
|
|
2 |
|
2 |
d |
(D) |
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
formulasına sáykes esaplanadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1-mısal. Shar belbewiniń betiniń maydanın tabıń. |
|
|
|
|
|||||||||||
Sheshiliwi. Orayı koordinata basında bolǵan, radiusı r ge teń |
sheńberiniń |
||||||||||||||
|
|
|
|
|
|||||||||||
y r2 x2 , a x b doǵası OX |
|
kósheriniń dógereginde aylanıwında payda |
|||||||||||||
bolǵan aylanba betlikke shar belbewı dep ataydı. Bul aylanba betliginiń maydanı
b |
|
|
|
|
|
x2 |
|
b |
|
|
(B) formulasına sáykes, P 2 |
r2 |
x2 |
1 |
|
dx 2 r dx 2 r(b a) . |
|||||
r2 x2 |
||||||||||
a |
|
|
|
|
|
a |
|
|||
|
|
|
|
|
|
|
||||
Bunnan a r, b r bolǵan |
dara |
|
jaǵdayında P 4 r 2 |
sfera betiniń |
||||||
maydanı kelip shıǵadı.
